28th Annual Computational Neuroscience Meeting: CNS*2019

doi:10.1186/s12868-019-0538-0

Volume 20 Supplement 1

28th Annual Computational Neuroscience Meeting: CNS*2019

Meeting Abstracts
Open Access
Published: 14 November 2019

28th Annual Computational Neuroscience Meeting: CNS*2019

BMC Neuroscience volume 20, Article number: 56 (2019) Cite this article

5460 Accesses
1 Altmetric
Metrics details

K1 Brain networks, adolescence and schizophrenia

Ed Bullmore

University of Cambridge, Department of Psychiatry, Cambridge, United Kingdom

Correspondence: Ed Bullmore (etb23@cam.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):K1

The adolescent transition from childhood to young adulthood is an important phase of human brain development and a period of increased risk for incidence of psychotic disorders. I will review some of the recent neuroimaging discoveries concerning adolescent development, focusing on an accelerated longitudinal study of ~ 300 healthy young people (aged 14–25 years) each scanned twice using MRI. Structural MRI, including putative markers of myelination, indicates changes in local anatomy and connectivity of association cortical network hubs during adolescence. Functional MRI indicates strengthening of initially weak connectivity of subcortical nuclei and association cortex. I will also discuss the relationships between intra-cortical myelination, brain networks and anatomical patterns of expression of risk genes for schizophrenia.

K2 Neural circuits for mental simulation

Kenji Doya

Okinawa Institute of Science and Technology, Neural Computation Unit, Okinawa, Japan

Correspondence: Kenji Doya (doya@oist.jp)

BMC Neuroscience 2019, 20(Suppl 1):K2

The basic process of decision making is often explained by learning of values of possible actions by reinforcement learning. In our daily life, however, we rarely rely on pure trial-and-error and utilize any prior knowledge about the world to imagine what situation will happen before taking an action. How such “mental simulation” is implemented by neural circuits and how they are regulated to avoid delusion are exciting new topics of neuroscience. Here I report our works with functional MRI in humans and two-photon imaging in mice to clarify how action-dependent state transition models are learned and utilized in the brain.

K3 One network, many states: varying the excitability of the cerebral cortex

Maria V. Sanchez-Vives

IDIBAPS and ICREA, Systems Neuroscience, Barcelona, Spain

Correspondence: Maria V. Sanchez-Vives (msanche3@clinic.cat)

BMC Neuroscience 2019, 20(Suppl 1):K3

In the transition from deep sleep, anesthesia or coma states to wakefulness, there are profound changes in cortical interactions both in the temporal and the spatial domains. In a state of low excitability, the cortical network, both in vivo and in vitro, expresses it “default activity pattern”, slow oscillations [1], a state of low complexity and high synchronization. Understanding the multiscale mechanisms that enable the emergence of complex brain dynamics associated with wakefulness and cognition while departing from low-complexity, highly synchronized states such as sleep, is key to the development of reliable monitors of brain state transitions and consciousness levels during physiological and pathological states. In this presentation I will discuss different experimental and computational approaches aimed at unraveling how the complexity of activity patterns emerges in the cortical network as it transitions across different brain states. Strategies such as varying anesthesia levels or sleep/awake transitions in vivo, or progressive variations in excitability by variable ionic levels, GABAergic antagonists, potassium blockers or electric fields in vitro, reveal some of the common features of these different cortical states, the gradual or abrupt transitions between them, and the emergence of dynamical richness, providing hints as to the underlying mechanisms.

Reference

1.
Sanchez-Vives, M, Marcello M, Maurizio M. Shaping the default activity pattern of the cortical network. Neuron 94.5 (2017): 993–1001.

K4 Neural circuits for flexible memory and navigation

Ila Fiete

Massachusetts Institute of Technology, McGovern Institute, Cambridge, United States of America

Correspondence: Ila Fiete (fiete@mit.edu)

BMC Neuroscience 2019, 20(Suppl 1):K4

I will discuss the problems of memory and navigation from a computational and functional perspective: What is difficult about these problems, which features of the neural circuit architecture and dynamics enable their solutions, and how the neural solutions are uniquely robust, flexible, and efficient.

F1 The geometry of abstraction in hippocampus and pre-frontal cortex

Silvia Bernardi¹, Marcus K. Benna², Mattia Rigotti³, Jérôme Munuera⁴, Stefano Fusi¹, C. Daniel Salzman¹

¹Columbia University, Zuckerman Mind Brain Behavior Institute, New York, United States of America; ²Columbia University, Center for Theoretical Neuroscience, Zuckerman Mind Brain Behavior Institute, New York, NY, United States of America; ³IBM Research AI, Yorktown Heights, United States of America, ⁴Columbia University, Centre National de la Recherche Scientifique (CNRS), École Normale Supérieure, Paris, France

Correspondence: Marcus K. Benna (mkb2162@columbia.edu)

BMC Neuroscience 2019, 20(Suppl 1):F1

Abstraction can be defined as a cognitive process that finds a common feature—an abstract variable, or concept—shared by a number of examples. Knowledge of an abstract variable enables generalization to new examples based upon old ones. Neuronal ensembles could represent abstract variables by discarding all information about specific examples, but this allows for representation of only one variable. Here we show how to construct neural representations that encode multiple abstract variables simultaneously, and we characterize their geometry. Representations conforming to this geometry were observed in dorsolateral pre-frontal cortex, anterior cingulate cortex, and the hippocampus in monkeys performing a serial reversal-learning task. These neural representations allow for generalization, a signature of abstraction, and similar representations are observed in a simulated multi-layer neural network trained with back-propagation. These findings provide a novel framework for characterizing how different brain areas represent abstract variables, which is critical for flexible conceptual generalization and deductive reasoning.

F2 Signatures of network structure in timescales of spontaneous activity

Roxana Zeraati¹, Nicholas Steinmetz², Tirin Moore³, Tatiana Engel⁴, Anna Levina⁵

¹University of Tübingen, International Max Planck Research School for Cognitive and System Neuroscience, Tübingen, Germany; ²University of Washington, Department of Biological Structure, Seattle, United States of America; ³Stanford University, Department of Neurobiology, Stanford, California, United States of America; ⁴Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, United States of America; ⁵University of Tübingen, Tübingen, Germany

Correspondence: Roxana Zeraati (roxana.zeraati@tuebingen.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):F2

Cortical networks are spontaneously active. Timescales of these intrinsic fluctuations were suggested to reflect the network’s specialization for task-relevant computations. However, how these timescales arise from the spatial network structure is unknown. Spontaneous cortical activity unfolds across different spatial scales. On a local scale of individual columns, ongoing activity spontaneously transitions between episodes of vigorous (On) and faint (Off) spiking, synchronously across cortical layers. On a wider spatial scale, activity propagates as cascades of elevated firing across many columns, characterized by the branching ratio defined as the average number of units activated by each active unit. We asked, to what extent the timescales of spontaneous activity reflect the dynamics on these two spatial scales and the underlying network structure. To this end, we developed a branching network model capable of capturing both the local On-Off dynamics and the global activity propagation. Each unit in the model represents a cortical column, which has spatially structured connections to other columns (Fig. 1A). The columns stochastically transition between On and Off states. Transitions to On-state are driven by stochastic external inputs and by excitatory inputs from the neighboring columns (horizontal recurrent input). An On state can persist due to a self-excitation representing strong recurrent connections within one column (vertical recurrent input). On and Off episode durations in our model follow exponential distributions, similar to the On-Off dynamics observed in single cortical columns (Fig. 1B). We fixed the statistics of On-Off transitions and the global propagation, and studied the dependence of intrinsic timescales on the network spatial structure.

We found that the timescales of local dynamics reflect the spatial network structure. In the model, activity of single columns exhibits two distinct timescales: one induced by the recurrent excitation within the column and another induced by interactions between the columns (Fig. 1C). The first timescale dominates dynamics in networks with more dispersed connectivity (Fig. 1A, non-local; Fig. 1D), whereas the second timescale is prominent in networks with more local connectivity (Fig. 1A, local; Fig. 1D). Since neighboring columns share many of their recurrent inputs, the second timescale is also evident in cross-correlations (CC) between columns, and it becomes longer with increasing distance between columns.

To test the model predictions, we analyzed 16-channel microelectrode array recordings of spiking activity from single columns in the primate area V4. During spontaneous activity, we observed two distinct timescales in columnar On-Off fluctuations (Fig. 1E). Two timescales were also present in CCs of neural activity on different channels within the same column. To examine how timescales depend on horizontal cortical distance, we leveraged the fact that columnar recordings generally exhibit slight horizontal shifts due to variability in the penetration angle. As a surrogate for horizontal displacements between pairs of channels, we used distances between centers of their receptive fields (RF). As predicted by the model, the second timescale in CCs became longer with increasing RF-center distance. Our results suggest that timescales of local On-Off fluctuations in single cortical columns provide information about the underlying spatial network structure of the cortex.

F3 Internal bias controls phasic but not delay-period dopamine activity in a parametric working memory task

Néstor Parga¹, Stefania Sarno¹, Manuel Beiran², José Vergara³, Román Rossi-Pool³, Ranulfo Romo³

¹Universidad Autónoma Madrid, Madrid, Spain; ²Ecole Normale Supérieure, Department of Cognitive Studies, Paris, France; ³Universidad Nacional Autónoma México, Instituto de Fisiología Celular, México DF, Mexico

Correspondence: Néstor Parga (nestor.parga@uam.es)

BMC Neuroscience 2019, 20(Suppl 1):F3

Dopamine (DA) has been implied in coding reward prediction errors (RPEs) and in several other phenomena such as working memory and motivation to work for reward. Under uncertain stimulation conditions DA phasic responses to relevant task cues reflect cortical perceptual decision-making processes, such as the certainty about stimulus detection and evidence accumulation, in a way compatible with the RPE hypothesis [1, 2]. This suggests that the midbrain DA system receives information from cortical circuits about decision formation and transforms it into an RPE signal. However, it is not clear how DA neurons behave when making a decision involves more demanding cognitive features, such as working memory and internal biases, or how they reflect motivation under uncertain conditions. To advance knowledge on these issues we have recorded and analyzed the firing activity of putatively midbrain DA neurons, while monkeys discriminated the frequencies of two vibrotactile stimuli delivered to one fingertip. This two-interval forced choice task, in which both stimuli were selected randomly in each trial, has been widely used to investigate perception, working memory and decision-making in sensory and frontal areas [3]; the current study adds to this scenario possible roles of midbrain DA neurons.

We found that the DA responses to the stimuli were not monotonically tuned to their frequency values. Instead they were controlled by an internally generated bias (contraction bias). This bias induced a subjective difficulty that modulated those responses as well as the accuracy and the response times (RTs). A Bayesian model for the choice explained the bias and gave a measure of the animal’s decision confidence, which also appeared modulated by the bias. We also found that the DA activity was above baseline throughout the delay (working memory) period. Interestingly, this activity was neither tuned to the first frequency nor controlled by the internal bias. While the phasic responses to the task events could be described by a reinforcement learning model based on belief states, the ramping behavior exhibited during the delay period could not be explained by standard models. Finally, the DA responses to the stimuli in short-RT trials and long-RTs trials were significantly different; interpreting the RTs as a measure of motivation, our analysis indicated that motivation affected strongly the responses to the task events but had only a weak influence on the DA activity during the delay interval. To summarize, our results show for the first time that an internal phenomenon (the bias) can control the DA phasic activity similar to the way physical differences in external stimuli do. We also encountered a ramping DA activity during the working memory period, independent of the memorized frequency value. Overall, our study supports the notion that delay and phasic DA activities accomplish quite different functions.

References

1.
Sarno S, de Lafuente V, Romo R, Parga N. Dopamine reward prediction error signal codes the temporal evaluation of a perceptual decision report. PNAS. 201712479 (2017)
2.
Lak A, Nomoto K, Keramati M, Sakagami M, Kepecs A. Midbrain dopamine neurons signal belief in choice accuracy during a perceptual decision. Curr Bio 27, 821–832 (2017)
3.
Romo R, Brody CD, Hernández A, Lemus L. Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 399, 470–473 (1999)

O1 Representations of dissociated shape and category in deep Convolutional Neural Networks and human visual cortex

Astrid Zeman, J Brendan Ritchie, Stefania Bracci, Hans Op de Beeck

KULeuven, Brain and Cognition, Leuven, Belgium

Correspondence: Astrid Zeman (astrid.zeman@kuleuven.be)

BMC Neuroscience 2019, 20(Suppl 1):O1

Deep Convolutional Neural Networks (CNNs) excel at object recognition and classification, with accuracy levels that now exceed humans [1]. In addition, CNNs also represent clusters of object similarity, such as the animate-inanimate division that is evident in object-selective areas of human visual cortex [2]. CNNs are trained using natural images, which contain shape and category information that is often highly correlated [3]. Due to this potential confound, it is therefore possible that CNNs rely upon shape information, rather than category, to classify objects. We investigate this possibility by quantifying the representational correlations of shape and category along the layers of multiple CNNs, with human behavioural ratings of these two factors, using two datasets that explicitly orthogonalize shape from category [3, 4] (Fig. 1a, b, c). We analyse shape and category representations along the human ventral pathway areas using fMRI (Fig. 1d) and measure correlations between artificial with biological representations by comparing the output from CNN layers with fMRI activation in ventral areas (Fig. 1e).

First, we find that CNNs encode object category independently from shape, which peaks at the final fully connected layer for all network architectures. At the initial layer of all CNNs, shape is represented significantly above chance in the majority of cases (94%), whereas category is not. Category information only increases above the significance level in the final few layers of all networks, reaching a maximum at the final layer after remaining low for the majority of layers. Second, by using fMRI to analyse shape and category representations along the ventral pathway, we find that shape information decreases from early visual cortex (V1) to the anterior portion of ventral temporal cortex (VTC). Conversely, category information increases from low to high from V1 to anterior VTC. This two-way interaction is significant for both datasets, demonstrating that this effect is evident for both low-level (orientation dependent) and high-level (low vs high aspect ratio) definitions of shape. Third, comparing CNNs with brain areas, the highest correlation with anterior VTC occurs at the final layer of all networks. V1 correlations reach a maximum prior to fully connected layers, at early, mid or late layers, depending upon network depth. In all CNNs, the order of maximum correlations with neural data corresponds well with the flow of visual information along the visual pathway. Overall, our results suggest that CNNs represent category information independently from shape, similarly to human object recognition processing.

References

1.
He K, Zhang X, Ren S, Sun J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. 2015 IEEE International Conference on Computer Vision (ICCV), Santiago 2015, pp 1026–1034.
2.
Khaligh-Razavi S-M, Kriegeskorte N. Deep Supervised, but Not Unsupervised, Models May Explain IT Cortical Representation. PLoS Computational Biology 2014, 10(11), e1003915.
3.
Bracci S, Op de Beeck H. Dissociations and Associations between Shape and Category. J Neurosci 2016, 36(2), 432–444.
4.
Ritchie JB, Op de Beeck H. Using neural distance to predict reaction time for categorizing the animacy, shape, and abstract properties of objects. BioRxiv 2018. Preprint at: https://doi.org/10.1101/496539

O2 Discovering the building blocks of hearing: a data-driven, neuro-inspired approach

Lotte Weerts¹, Claudia Clopath², Dan Goodman¹

¹Imperial College London, Electrical and Electronic Engineering, London, United Kingdom; ²Imperial College London, Department of Bioengineering, London, United Kingdom

Correspondence: Dan Goodman (d.goodman@imperial.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):O2

Our understanding of hearing and speech recognition rests on controlled experiments requiring simple stimuli. However, these stimuli often lack the variability and complexity characteristic of complex sounds such as speech. We propose an approach that combines neural modelling with data-driven machine learning to determine auditory features that are both theoretically powerful and can be extracted by networks that are compatible with known auditory physiology. Our approach bridges the gap between detailed neuronal models that capture specific auditory responses, and research on the statistics of real-world speech data and its relationship to speech recognition. Importantly, our model can capture a wide variety of well studied features using specific parameter choices, and allows us to unify several concepts from different areas of hearing research.

We introduce a feature detection model with a modest number of parameters that is compatible with auditory physiology. We show that this model is capable of detecting a range of features such as amplitude modulations (AMs) and onsets. In order to objectively determine relevant feature detectors within our model parameter space, we use a simple classifier that approximates the information bottleneck, a principle grounded in information theory that can be used to define which features are “useful”. By analysing the performance in a classification task, our framework allows us to determine the best model parameters and their neurophysiological implications and relate those to psychoacoustic findings.

We analyse the performance of a range of model variants in a phoneme classification task (Fig. 1). Some variants improve accuracy compared to using the original signal, indicating that our feature detection model extracts useful information. By analysing the properties of high performing variants, we rediscover several proposed mechanisms for robust speech processing. Firstly, our result suggest that model variants that can detect and distinguish between formants are important for phoneme recognition. Secondly, we rediscover the importance of AM sensitivity for consonant recognition, which is in line with several experimental studies that show that consonant recognition is degraded when certain amplitude modulations are removed. Besides confirming well-known mechanisms, our analysis hints at other less-established ideas, such as the importance of onset suppression. Our results indicate that onset suppression can improve phoneme recognition, which is in line with the hypothesis that the suppression of onset noise (or “spectral splatter”), as observed in the mammalian auditory brainstem, can improve the clarity of a neural harmonic representation. We also discover model variants that are responsive to more complex features, such as combined onset and AM sensitivity. Finally, we show how our approach lends itself to be extended to more complex environments, by distorting the clean speech signal with noise.

Our approach has various potential applications. Firstly, it could lead to new, testable experimental hypotheses for understanding hearing. Moreover, promising features could be directly applied as a new acoustic front-end for speech recognition systems.

Acknowledgments: This work was partly supported by a Titan Xp donated by the NVIDIA Corporation, The Royal Society grant RG170298 and the Engineering and Physical Sciences Research Council (grant number EP/L016737/1).

O3 Modeling stroke and rehabilitation in mice using large-scale brain networks

Spase Petkoski¹, Anna Letizia Allegra Mascaro², Francesco Saverio Pavone², Viktor Jirsa¹

¹Aix-Marseille Université, Institut de Neurosciences des Systèmes, Marseille, France; ²University of Florence, European Laboratory for Non-linear Spectroscopy, Florence, Italy

Correspondence: Spase Petkoski (spase.petkoski@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):O3

Individualized large-scale computational modeling of the dynamics associated with the brain pathologies [1] is an emerging approach in the clinical applications, which gets validation through animal models. A good candidate for confirmation of brain network causality is stroke and the subsequent recovery, which alter brain’s structural connectivity, and this is then reflected on functional and behavioral level. In this study we use large-scale brain network model (BNM) to computationally validate the structural changes due to stroke and recovery in mice, and their impact on the resting state functional connectivity (FC), as captured by wide-field calcium imaging.

We built our BNM based on the detailed Allen Mouse (AM) connectome that is implemented in The Virtual Mouse Brain [2]. It dictates the strength of the couplings between distant brain regions based on tracer data. The homogeneous local connectivity is absorbed into the neuronal mass model that is generally derived from mean activity of populations of spiking neurons, Fig. 1, and is here represented by the Kuramoto oscillators [3], as canonical model for network synchronization due to weak interactions. The photothrombotic focal stroke affects the right primary motor cortex (rM1). The injured forelimb is daily trained on a custom designed robotic device (M-Platform, [4, 5]) from 5 days after the stroke for a total of 4 weeks. The stroke is modeled by different levels of damage of the links connecting rM1, while the recovery is represented by reinforcing of alternative connections of the nodes initially linked to it [6]. We systematically simulate various impacts of stroke and recovery, to find the best match with the coactivation patterns in the data, where the FC is characterized with the phase coherence calculated for the phases of Hilbert transformed delta frequency activity of pixels within separate regions [6]. Statistically significant changes within the FC of 5 animals are obtained for transitions between the three conditions: healthy, stroke and rehabilitation after 4 weeks of training, and these are compared with the best fits for each condition of the model in the parameter’s space of the global coupling strength and stroke impact and rewiring.

This approach uncovers recovery paths in the parameter space of the dynamical system that can be related to neurophysiological quantities such as the white matter tracts. This can lead to better strategies for rehabilitation, such as stimulation or inhibition of certain regions and links that have a critical role on the dynamics of the recovery.

References

1.
Olmi S, Petkoski S, Guye M, Bartolomei F, Jirsa V. Controlling seizure propagation in large-scale brain networks. PLoS Comp Biol. [in press]
2.
Melozzi F, Woodman MM, Jirsa VK, Bernard C. The Virtual Mouse Brain: A computational neuroinformatics platform to study whole mouse brain dynamics. eNeuro 0111-17. 2017.
3.
Petkoski S, Palva JM, Jirsa VK. Phase-lags in large scale brain synchronization: Methodological considerations and in-silico analysis. PLoS Comp Biol, 14(7), 1–30. 2018.
4.
Spalletti C, et al. A robotic system for quantitative assessment and poststroke training of forelimb retraction in mice. Neurorehabilitation and neural repair 28, 188–196. 2014.
5.
Allegra Mascaro, A et al. Rehabilitation promotes the recovery of distinct functional and structural features of healthy neuronal networks after stroke. [under review].
6.
Petkoski S, et al. Large-scale brain network model for stroke and rehabilitation in mice. [in prep].

O4 Self-consistent correlations of randomly coupled rotators in the asynchronous state

Alexander van Meegen¹, Benjamin Lindner²

¹Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6) and Institute for Advanced Simulation (IAS-6), Jülich, Germany; ²Humboldt University Berlin, Physics Department, Berlin, Germany

Correspondence: Alexander van Meegen (a.van.meegen@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):O4

Spiking activity of cortical neurons in behaving animals is highly irregular and asynchronous. The quasi stochastic activity (the network noise) does not seem to root in the comparatively weak intrinsic noise sources but is most likely due to the nonlinear chaotic interactions in the network. Consequently, simple models of spiking neurons display similar states, the theoretical description of which has turned out to be notoriously difficult. In particular, calculating the neuron’s correlation function is still an open problem. One classical approach pioneered in the seminal work of Sompolinsky et al. [1] used analytically tractable rate units to obtain a self-consistent theory of the network fluctuations and the correlation function of the single unit in the asynchronous irregular state. Recently, the original model attracted renewed interest, leading to substantial extensions and a wide range of novel results [2–5].

Here, we develop a theory for a heterogeneous random network of unidirectionally coupled phase oscillators [6]. Similar to Sompolinsky’s rate-unit model, the system can attain an asynchronous state with pronounced temporal autocorrelations of the units. The model can be examined analytically and even allows for closed-form solutions in simple cases. Furthermore, with a small extension, it can mimic mean-driven networks of spiking neurons and the theory can be extended to this case accordingly.

Specifically, we derived a differential equation for the self-consistent autocorrelation function of the network noise and of the single oscillators. Its numerical solution has been confirmed by simulations of sparsely connected networks (Fig. 1). Explicit expressions for correlation functions and power spectra for the case of a homogeneous network (identical oscillators) can be obtained in the limits of weak or strong coupling strength. To apply the model to networks of sparsely coupled excitatory and inhibitory exponential integrate-and-fire (IF) neurons, we extended the coupling function and derived a second differential equation for the self-consistent autocorrelations. Deep in the mean-driven regime of the spiking network, our theory is in excellent agreement with simulations results of the sparse network.

This work paves the way for more detailed studies of how the statistics of connection strength, the heterogeneity of network parameters, and the form of the interaction function shape the network noise and the autocorrelations of the single element in asynchronous irregular state.

References

1.
Sompolinsky H, Crisanti A, Sommers HJ. Chaos in random neural networks. Physical review letters 1988 Jul 18;61(3):259.
2.
Kadmon J, Sompolinsky H. Transition to chaos in random neuronal networks. Physical Review X 2015 Nov 19;5(4):041030.
3.
Mastrogiuseppe F, Ostojic S. Linking connectivity, dynamics, and computations in low-rank recurrent neural networks. Neuron 2018 Aug 8;99(3):609-23.
4.
Schuecker J, Goedeke S, Helias M. Optimal sequence memory in driven random networks. Physical Review X 2018 Nov 14;8(4):041029.
5.
Muscinelli SP, Gerstner W, Schwalger T. Single neuron properties shape chaotic dynamics in random neural networks. arXiv preprint arXiv:1812.06925 2018 Dec 17.
6.
van Meegen A, Lindner B. Self-Consistent Correlations of Randomly Coupled Rotators in the Asynchronous State. Physical review letters 2018 Dec 20;121(25):258302.

O5 Firing rate-dependent phase responses dynamically regulate Purkinje cell network oscillations

Yunliang Zang, Erik De Schutter

Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Onna-Son, Japan

Correspondence: Yunliang Zang (zangyl1983@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O5

Phase response curves (PRCs) have been defined to quantify how a weak stimulus shift the next spike timing in regular firing neurons. However, the biophysical mechanisms that shape the PRC profiles are poorly understood. The PRCs in Purkinje cells (PCs) show firing rate (FR) adaptation. At low FRs, the responses are small and phase independent. At high FRs, the responses become phase dependent at later phases, with their onset phases gradually left-shifted and peaks gradually increased, due to an unknown mechanism [1, 2].

Using our recently developed compartment-based PC model [3], we reproduced the FR-dependence of PRCs and identified the depolarized interspike membrane potential as the mechanism underlying the transition from phase-independent responses at low FRs to the gradually left-shifted phase-dependent responses at high FRs. We also demonstrated this mechanism plays a general role in shaping PRC profiles in other neurons.

PC axon collaterals have been proposed to correlate temporal spiking in PC ensembles [4, 5], but whether and how they interact with the FR-dependent PRCs to regulate PC output remains unexplored. We built a recurrent inhibitory PC-to-PC network model to examine how FR-dependent PRCs regulate the synchrony of high frequency (~ 160 Hz) oscillations observed in vivo [4]. We find the synchrony of these oscillations increases with FR due to larger and broader PRCs at high FRs. This increased synchrony still holds when the network incorporates dynamically and heterogeneously changing cellular FRs. Our work implies that FR-dependent PRCs may be a critical property of the cerebellar cortex in combining rate- and synchrony-coding to dynamically organize its temporal output.

References

1.
Phoka E., et al., A new approach for determining phase response curves reveals that Purkinje cells can act as perfect integrators. PLoS Comput. Biol 2010. 6(4): p. e1000768.
2.
Couto J., et al., On the firing rate dependency of the phase response curve of rat Purkinje neurons in vitro. PLoS Comput. Biol 2015. 11(3): p. e1004112.
3.
Zang Y, Dieudonne S, De Schutter E. Voltage- and Branch-Specific Climbing Fiber Responses in Purkinje Cells. Cell Rep 2018. 24(6): p. 1536-1549.
4.
de Solages C., et al., High-frequency organization and synchrony of activity in the purkinje cell layer of the cerebellum. Neuron 2008. 58(5): p. 775-88.
5.
Witter L., et al., Purkinje Cell Collaterals Enable Output Signals from the Cerebellar Cortex to Feed Back to Purkinje Cells and Interneurons. Neuron 2016. 91(2): p. 312-9.

O6 Computational modeling of brainstem-spinal circuits controlling locomotor speed and gait

Ilya Rybak, Jessica Ausborn, Simon Danner, Natalia Shevtsova

Drexel University College of Medicine, Department of Neurobiology and Anatomy, Philadelphia, PA, United States of America

Correspondence: Ilya Rybak (rybak@drexel.edu)

BMC Neuroscience 2019, 20(Suppl 1):O6

Locomotion is an essential motor activity allowing animals to survive in complex environments. Depending on the environmental context and current needs quadruped animals can switch locomotor behavior from slow left-right alternating gaits, such as walk and trot (typical for exploration), to higher-speed synchronous gaits, such as gallop and bound (specific for escape behavior). At the spinal cord level,the locomotor gait is controlled by interactions between four central rhythm generators (RGs) located on the left and right sides of the lumbar and cervical enlargements of the cord, each producing rhythmic activity controlling one limb. The activities of the RGs are coordinated by commissural interneurons (CINs), projecting across the midline to the contralateral side of the cord, and long propriospinal neurons (LPNs), connecting the cervical and lumbar circuits. At the brainstem level, locomotor behavior and gaitsare controlled by two majorbrainstem nuclei: the cuneiform (CnF) and the pedunculopontine (PPN) nuclei [1]. Glutamatergic neurons in both nuclei contribute to the control of slow alternating-gait movements, whereas only activation of CnF can elicit high-speed synchronous-gait locomotion. Neurons from both regions project to the spinal cord via descendingreticulospinal tracts from thelateral paragigantocellular nuclei (LPGi) [2].

To investigate the brainstem control of spinal circuits involved in the slow exploratory and fast escape locomotion, we built a computational model ofthe brainstem-spinal circuits controlling these locomotor behaviors. The spinal cord circuits in the modelincluded four RGs (one per limb) interacting via cervical and lumbar CINs and LPNs. The brainstem model incorporated bilaterally interacting CnF and PPN circuits projecting to the LPGi nuclei that mediated the descending pathways to the spinal cord.These pathways provided excitation of all RGs to control locomotor frequency and inhibited selected CINs and LPNs, which allowed the model to reproduce the speed-dependent gait transitions observed in intact mice and the loss of particular gaits in mutants lacking some genetically identified CINs [3].The proposed structure of synaptic inputs of the descending (LPGi) pathways to the spinal CINs and LPNs allowed the model to reproduce the experimentally observed effects of stimulation of excitatory and inhibitory neurons within CnF, PPN, and LPGi. The suggests explanations for (a) the speed-dependent expression of different locomotor gaits and the role of different CINs and LPNs in gait transitions, (b) the involvement of the CnF and PPN nuclei in the control of low-speed alternating-gait locomotion and the specific role of the CnF in the control of high-speed synchronous-gait locomotion, and (c) the role of inhibitory neurons in these areas in slowing down and stopping locomotion. The model provides important insights into the brainstem-spinal cord interactions and the brainstem control of locomotor speed and gaits.

References

1.
Caggiano V, Leiras R, Goñi-Erro H, et al. Midbrain circuits that set locomotor speed and gait selection. Nature 2018, 553, 455–460.
2.
Capelli P, Pivetta C, Esposito MS, Arber S. Locomotor speed control circuits in the caudal brainstem. Nature 2017, 551, 373–377.
3.
Bellardita C, Kiehn O. Phenotypic characterization of speed-associated gait changes in mice reveals modular organization of locomotor networks. Curr Biol 2015, 25, 1426–1436.

O7 Co-refinement of network interactions and neural response properties in visual cortex

Sigrid Trägenap¹, Bettina Hein¹, David Whitney², Gordon Smith³, David Fitzpatrick², Matthias Kaschube¹

¹Frankfurt Institute for Advanced Studies (FIAS), Department of Neuroscience, Frankfurt, Germany; ²Max Planck Florida Institute, Department of Neuroscience, Jupiter, FL, United States of America; ³University of Minnesota, Department of Neuroscience, Minneapolis, MN, United States of America

Correspondence: Sigrid Trägenap (traegenap@fias.uni-frankfurt.de)

BMC Neuroscience 2019, 20(Suppl 1):O7

In the mature visual cortex, local tuning properties are linked through distributed network interactions with a remarkable degree of specificity [1]. However, it remains unknown whether the tight linkage between functional tuning and network structure is an intrinsic feature of cortical circuits, or instead gradually emerges in development. Combining virally-mediated expression of GCAMP6s in pyramidal neurons with wide-field epifluorescence imaging in ferret visual cortex, we longitudinally monitored the spontaneous activity correlation structure—our proxy for intrinsic network interactions- and the emergence of orientation tuning around eye-opening.

We find that prior to eye-opening, the layout of emerging iso-orientation domains is only weakly similar to the spontaneous correlation structure. Nonetheless within one week of visual experience, the layout of iso-orientation domains and the spontaneous correlation structure become rapidly matched. Motivated by these observations, we developed dynamical equations to describe how tuning and network correlations co-refine to become matched with age. Here we propose an objective function capturing the degree of consistency between orientation tuning and network correlations. Then by gradient descent of this objective function, we derive dynamical equations that predict an interdependent refinement of orientation tuning and network correlations. To first approximation, these equations predict that correlated neurons become more similar in orientation tuning over time, while network correlations follow a relaxation process increasing the degree of self-consistency in their link to tuning properties.

Empirically, we indeed observe a refinement with age in both orientation tuning and spontaneous correlations. Furthermore, we find that this framework can utilize early measurements of orientation tuning and correlation structure to predict aspects of the future refinement in orientation tuning and spontaneous correlations. We conclude that visual response properties and network interactions show a considerable degree of coordinated and interdependent refinement towards a self-consistent configuration in the developing visual cortex.

Reference

1.
Smith GB, Hein B, Whitney DE, Fitzpatrick D, Kaschube M. Distributed network interactions and their emergence in developing neocortex. Nature Neuroscience 2018 Nov;21(11):1600.

O8 Receptive field structure of border ownership-selective cells in response to direction of figure

Ko Sakai¹, Kazunao Tanaka¹, Rüdiger von der Heydt², Ernst Niebur³

¹University of Tsukuba, Department of Computer Science, Tsukuba, Japan; ²Johns Hopkins University, Krieger Mind/Brain Institute, Baltimore, United States of America; ³Johns Hopkins, Neuroscience, Baltimore, MD, United States of America

Correspondence: Ko Sakai (sakai@cs.tsukuba.ac.jp)

BMC Neuroscience 2019, 20(Suppl 1):O8

The responses of border ownership-selective cells (BOCs) have been reported to signal the direction of figure (DOF) along the contours in natural images with a variety of shapes and textures [1]. We examined the spatial structure of the optimal stimuli for BOCs in monkey visual cortical area V2 to determine the structure of the receptive field. We computed the spike triggered average (STA) from responses of the BOCs to natural images (JHU archive, http://dx.doi.org/10.7281/T1C8276W). To estimate the STA in response to figure-ground organization of natural images, we tagged figure regions with luminance contrast. The left panel in Fig 1 illustrates the procedure for STA computation. We first aligned all images to a given cell’s preferred orientation and preferred direction of figure. We then grouped the images based on the luminance contrast of their figure regions with respect to their ground regions, and averaged them separately for each group. By averaging the bright-figure stimuli with weights based on each cell’s spike count, we were able to observe the optimal figure and ground sub-regions as brighter and darker regions, respectively. By averaging the dark-figure stimuli, we obtained the reverse. We then generated the STA by subtracting the average of the dark-figure stimuli from that of the bright-figure stimuli. This subtraction canceled out the dependence of response to contrast. We compensated for the bias due to the non-uniformity of luminance in the natural images by subtracting the simple ensemble average of the stimuli (equivalent to weight = 1 for all stimuli) from the weighted average. The mean STA across 22 BOCs showed facilitated and suppressed sub-regions in response to the figure towards the preferred and non-preferred DOFs, respectively (Fig. 1, the right panel). The structure was shown more clearly when figure and ground were replaced by a binary mask. The result demonstrates, for the first time, the antagonistic spatial structure in the receptive field of BOCs in response to figure-ground organization.

Acknowledgment: This work was partly supported by JSPS (KAKENHI, 26280047, 17H01754) and National Institutes of Health (R01EY027544 and R01DA040990).

Reference

1.
Williford JR, Von Der Heydt R. Figure-ground organization in visual cortex for natural scenes. eNeuro 2016 Nov; 3(6) 1–15

O9 Development of periodic and salt-and-pepper orientation maps from a common retinal origin

Min Song, Jaeson Jang, Se-Bum Paik

Korea Advanced Institute of Science and Technology, Department of Biology and Brain Engineering, Daejeon, South Korea

Correspondence: Min Song (night@kaist.ac.kr)

BMC Neuroscience 2019, 20(Suppl 1):O9

Spatial organization of orientation tuning in the primary visual cortex (V1) is arranged in different forms across mammalian species. In some species (e.g. monkeys or cats), the preferred orientation continuously changes across the cortical surface (columnar orientation map), while other species (e.g. mice or rats) have a random-like distribution of orientation preference, termed salt-and-pepper organization. However, it still remains unclear why the organization of the cortical circuit develops differently across species. Previously, it was suggested that each type of circuit might be a result of wiring optimization under different conditions of evolution [1], but the developmental mechanism of each organization of orientation tuning still remains unclear. In this study, we propose that the structural variations between cortical circuits across species simply arise from the differences in physical constraints of the visual system—the size of the retina and V1 (see Fig. 1). By expanding the statistical wiring model proposing that the orientation tuning of a V1 neuron is restricted by the local arrangement of ON and OFF retinal ganglion cells (RGCs) [2, 3], we suggest that the number of V1 neurons sampling a given RGC (sampling ratio) is a crucial factor in determining the continuity of orientation tuning in V1. Our simulation results show that as the sampling ratio increases, neighboring V1 neurons receive similar retinal inputs, resulting in continuous changes in orientation tuning. To validate our prediction, we estimated the sampling ratio of each species from the physical size of the retina and V1 [5] and compared with the organization of orientation tuning. As predicted, this ratio could successfully distinguish diverse mammalian species into two groups according to the organization of orientation tuning, even though the organization has not been clearly predicted by considering only a single factor in the visual system (e.g. V1 size or visual acuity; [4]). Our results suggest a common retinal origin of orientation preference across diverse mammalian species, while its spatial organization can vary depending on the physical constraints of the visual system.

References

1.
Kaschube M. Neural maps versus salt-and-pepper organization in visual cortex. Current opinion in neurobiology 2014, 24: 95-102.
2.
Ringach DL. “Haphazard wiring of simple receptive fields and orientation columns in visual cortex.” Journal of neurophysiology 2004, 92.1: 468-476.
3.
Ringach DL. On the origin of the functional architecture of the cortex. PloS one 2007, 2.2: e251.
4.
Van Hooser SD, et al. Orientation selectivity without orientation maps in visual cortex of a highly visual mammal. Journal of Neuroscience 2005, 25.1: 19-28.
5.
Colonnese MT, et al. A conserved switch in sensory processing prepares developing neocortex for vision. Neuron 2010, 67.3: 480-498.

O10 Explaining the pitch of FM-sweeps with a predictive hierarchical model

Alejandro Tabas¹, Katharina von Kriegstein²

¹Max Planck Institute for Human Cognitive and Brain Sciences, Research Group in Neural Mechanisms of Human Communication, Leipzig, Germany; ²Tesnische Universität Dresden, Chair of Clinical and Cognitive Neuroscience, Faculty of Psychology, Dresden, Germany

Correspondence: Alejandro Tabas (alextabas@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O10

Frequency modulation (FM) is a basic constituent of vocalisation. FM-sweeps in the frequency range and modulation rates of speech have been shown to elicit a pitch percept that consistently deviates from the sweep average frequency [1]. Here, we use this perceptual effect to inform a model characterising the neural encoding of FM.

First, we performed a perceptual experiment where participants were asked to match the pitch of 30 sweeps with probe sinusoids of the same duration. The elicited pitch systematically deviated from the average frequency of the sweep by an amount that depended linearly on the modulation slope. Previous studies [2] have proposed that the deviance might be due to a fixed-sized-window integration process that fosters frequencies present at the end of the stimulus. To test this hypothesis, we conducted a second perceptual experiment considering the pitch elicited by continuous trains of five concatenated sweeps. As before, participants were asked to match the pitch of the sweep trains with probe sinusoids. Our results showed that the pitch deviance from the mean observed in sweeps was severely reduced in the train stimuli, in direct contradiction with the fixed-sized-integration-window hypothesis.

The perceptual effects may also stem from unexpected interactions between the frequencies spanned in the stimuli during pitch processing. We studied this posibility in two well-established families of mechanistic models of pitch. First, we considered a general spectral model that computes pitch as the expected value of the activity distribution across the cochlear decomposition. Due to adaptation effects, this model fostered the spectral range present at the beginning of the sweep: the exact opposite of what we observed in the experimental data. Second, we considered the predictions of the summary autocorrelation function (SACF) [3], a prototypical model of temporal pitch processing that considers the temporal structure of the auditory nerve activity. The SACF was unable to integrate temporal pitch information quickly enough to keep track of the modulation rate, yielding inconsistent pitch predictions that deviated stochastically from the average frequency.

Here, we introduce an alternative hypothesis based on top-down facilitation. Top-down efferents constitute an important fraction of the fibres in the auditory nerve; moreover, top-down predictive facilitation may reduce the metabolic cost and increase the speed of the neural encoding of expected inputs. Our model incorporates a second layer of neurons encoding FM direction that, after detecting that the incoming inputs are consistent with a rising (falling) sweep, anticipate that neurons encoding immediately higher (lower) frequencies will activate next. This prediction is propagated downwards to neurons encoding such frequencies, increasing their readiness and effectively inflating their weight during pitch temporal integration.

The described mechanism fully reproduces our and previously published experimental results (Fig. 1). We conclude that top-down predictive modulation plays an important role in the neural encoding of frequency modulation even at early stages of the processing hierarchy.

References

1.
d’Alessandro C, Castellengo M. The pitch of short‐duration vibrato tones. The Journal of the Acoustical Society of America 1994 Mar;95(3):1617-30.
2.
Brady PT, House AS, Stevens KN. Perception of sounds characterized by a rapidly changing resonant frequency. The Journal of the Acoustical Society of America 1961 Oct;33(10):1357-62.
3.
Meddis R, O’Mard LP. Virtual pitch in a computational physiological model. The Journal of the Acoustical Society of America 2006 Dec;120(6):3861-9.

O11 Effects of anesthesia on coordinated neuronal activity and information processing in rat primary visual cortex

Heonsoo Lee, Shiyong Wang, Anthony Hudetz

University of Michigan, Anesthesiology, Ann Arbor, MI, United States of America

Correspondence: Heonsoo Lee (heonslee@umich.edu)

BMC Neuroscience 2019, 20(Suppl 1):O11

Introduction: Understanding of how anesthesia affects neural activity is important to reveal the mechanism of loss and recovery of consciousness. Despite numerous studies during the past decade, how anesthesia alters spiking activity of different types of neurons and information processing within an intact neural network is not fully understood. Based on prior in vitro studies we hypothesized that excitatory and inhibitory neurons in neocortex are differentially affected by anesthetic. We also predicted that individual neurons are constrained to population activity, leading to impaired information processing within a neural network.

Methods: We implanted sixty-four-contact microelectrode arrays in primary visual cortex (layer 5/6, contacts spanning 800 µm depth and 1600 µm width) for recording of extracellular unit activity at three steady-state levels of anesthesia (6, 4 and 2% desflurane) and wakefulness (number of rats = 8). Single unit activities were extracted and putative excitatory and inhibitory neurons were identified based on their spike waveforms and autocorrelogram characteristics (number of neurons = 210). Neuronal features such as firing rate, interspike interval (ISI), bimodality, and monosynaptic spike transmission probabilities were investigated. Normalized mutual information and transfer entropy were also applied to investigate the interaction between spike trains and population activity (local field potential; LFP).

Results: First, anesthesia significantly altered characteristics of individual neurons. Firing rate of most neurons was reduced; this effect was more pronounced in inhibitory neurons. Excitatory neurons showed enhanced bursting activity (ISI<9 ms) and silent periods (hundreds of milliseconds) (Fig. 1A). Second, anesthesia disrupted information processing within a neural network. Neurons shared the silent periods, resulting in synchronous population activity (neural oscillations), despite of the suppressed monosynaptic connectivity (Fig. 1B). The population activity (LFP) showed reduced information content (entropy), and was easily predicted by individual neurons; that is, shared information between individual neurons and population activity was significantly increased (Fig. 1C). Transfer entropy analysis revealed a strong directional influence from LFP to individual neurons, suggesting that neuronal activity is constrained to the synchronous population activity.

Conclusions: This study reveals how excitatory and inhibitory neurons are differentially affected by anesthetic, leading to synchronous population activity and impaired information processing. These findings provide an integrated understanding of anesthetic effects on neuronal activity and information processing. Further study of stimulus evoked activity and computational modeling will provide a more detailed mechanism of how anesthesia alters neural activity and disrupts information processing.

O12 Learning where to look: a foveated visuomotor control model

Emmanuel Daucé¹, Pierre Albigès², Laurent Perrinet³

¹Aix-Marseille Univ, INS, Marseille, France; ²Aix-Marseille Univ, Neuroschool, Marseille, France; ³CNRS - Aix-Marseille Université, Institut de Neurosciences de la Timone, Marseille, France

Correspondence: Emmanuel Daucé (emmanuel.dauce@centrale-marseille.fr)

BMC Neuroscience 2019, 20(Suppl 1):O12

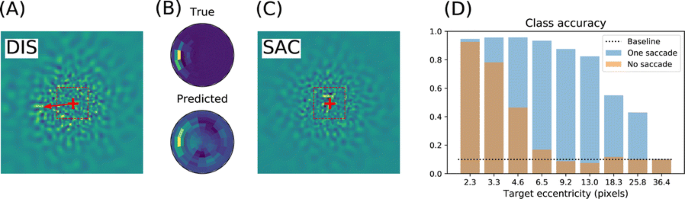
We emulate a model of active vision which aims at finding a visual target whose position and identity are unknown. This generic visual search problem is of broad interest to machine learning, computer vision and robotics, but also to neuroscience, as it speaks to the mechanisms underlying foveation and more generally to low-level attention mechanisms. From a computer vision perspective, the problem is generally addressed by processing the different hypothesis (categories) at all possible spatial configuration through dedicated parallel hardware. The human visual system, however, seems to employ a different strategy, through a combination of a foveated sensor with the capacity of rapidly moving the center of fixation using saccades. Visual processing is done through fast and specialized pathways, one of which mainly conveying information about target position and speed in the peripheral space (the “where” pathway), the other mainly conveying information about the identity of the target (the “what” pathway). The combination of the two pathways is expected to provide most of the useful knowledge about the external visual scene. Still, it is unknown why such a separation exists. Active vision methods provide the ground principles of saccadic exploration, assuming the existence of a generative model from which both the target position and identity can be inferred through active sampling. Taking for granted that (i) the position and category of objects are independent and (ii) the visual sensor is foveated, we consider how to minimize the overall computational cost of finding a target. This justifies the design of two complementary processing pathways: first a classical image classifier, assuming that the gaze is on the object, and second a peripheral processing pathway learning to identify the position of a target in retinotopic coordinates. This framework was tested on a simple task of finding digits in a large, cluttered image (see Fig. 1). Results demonstrate the benefit of specifically learning where to look, and this before actually identifying the target category (with cluttered noise ensuring the category is not readable in the periphery). In the “what” pathway, the accuracy drops to the baseline at mere 5 pixels away from the center of fixation, while issuing a saccade is beneficial in up to 26 pixels around, allowing a much wider covering of the image. The difference between the two distributions forms an “accuracy gain”, that quantifies the benefit of issuing a saccade with respect to a central prior. Until the central classifier is confident, the system should thus perform a saccade to the most likely target position. The different accuracy predictions, such as the ones done in the “what” and the “where” pathway, may also explain more elaborate decision making, such as the inhibition of return. The approach is also energy-efficient as it includes the strong compression rate performed by retina and V1 encoding, which is preserved up to the action selection level. The computational cost of this active inference strategy may thus be way less than that of a brute force framework. This provides evidence of the importance of identifying “putative interesting targets” first and we highlight some possible extensions of our model both in computer vision and modeling.

O13 A standardized formalism for voltage-gated ion channel models

Chaitanya Chintaluri¹, Bill Podlaski², Pedro Goncalves³, Jan-Matthis Lueckmann³, Jakob H. Macke³, Tim P. Vogels¹

¹University of Oxford, Centre for Neural Circuits and Behaviour, Oxford, United Kingdom; ²Champalimaud Center for the Unknown, Lisbon, Portugal; ³Research Center Caesar; Technical University of Munich, Bonn, Germany

Correspondence: Bill Podlaski (william.podlaski@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O13

Biophysical neuron modelling has become widespread in neuroscience research, with the combination of diverse ion channel kinetics and morphologies being used to explain various single-neuron properties. However, there is no standard by which ion channel models are constructed, making it very difficult to relate models to each other and to experimental data. The complexity and scale of these models also makes them especially susceptible to problems with reproducibility and reusability, especially when translating between different simulators. To address these issues, we revive the idea of a standardised model for ion channels based on a thermodynamic interpretation of the Hodgkin-Huxley formalism, and apply it to a recently curated database of approximately 2500 published ion channel models (ICGenealogy). We show that a standard formulation fits the steady-state and time-constant curves of nearly all voltage-gated models found in the database, and reproduces responses to voltage-clamp protocols with high fidelity, thus serving as a functional translation of the original models. We further test the correspondence of the standardised models in a realistic physiological setting by simulating the complex spiking behaviour of multi-compartmental single-neuron models in which one or several of the ion channel models are replaced by the corresponding best-fit standardised model. These simulations result in qualitatively similar behaviour, often nearly identical to the original models. Notably, when differences do arise, they likely reflect the fact that many of the models are very finely tuned. Overall, this standard formulation facilitates be er understanding and comparisons among ion channel models, as well as reusability of models through easy functional translation between simulation languages. Additionally, our analysis allows for a direct comparison of models based on parameter settings, and can be used to make new observations about the space of ion channel kinetics across different ion channel subtypes, neuron types and species.

O14 A priori identifiability of a binomial synapse

Camille Gontier¹, Jean-Pascal Pfister²

¹University of Bern, Department of Physiology, Bern, France; ²University of Bern, Department of Physiology, Bern, Switzerland

Correspondence: Camille Gontier (gontier@pyl.unibe.ch)

BMC Neuroscience 2019, 20(Suppl 1):O14

Synapses are highly stochastic transmission units. A classical model describing this transmission is called the binomial model [1], which assumes that there are N independent release sites, each having the same release probability p; and that each vesicle release gives rise to a quantal current q. The parameters of the binomial model (N, p, q, and the recording noise) can be estimated from postsynaptic responses, either by following a maximum-likelihood approach [2] or by computing the posterior distribution over the parameters [3].

But these estimates might be subject to parameter identifiability issues. This uncertainty of the parameter estimates is usually assessed a posteriori from recorded data, for instance by using re-sampling procedure such as parametric bootstrap.

Here, we propose a methodology for a priori quantifying the structural identifiability of the parameters. A lower bound on the error of parameter estimates can be obtained analytically using the Cramer-Rao bound. Instead of simply assessing a posteriori the validity of their parameter estimates, it is thus possible for experimentalists to select a priori a lower bound on the standard deviation of the estimates and to select the number of data points and to tune the level of noise accordingly.

Besides parameter identifiability, another critical issue is the so-called model identifiability, i.e. the possibility, given a certain number of data points T and a certain level of measurement noise, to find the model of synapse that fits our data the best. For instance, when observing discrete peaks on the histogram of post-synaptic currents, one might be tempted to conclude that the binomial model (“multi-quantal hypothesis”) is the best one to fit the data. However, these peaks might actually be artifacts due to noisy or scarce data points, and data might be best explained by a simpler Gaussian distribution (“uni-quantal hypothesis”).

Model selection tools are classically used to determine a posteriori which model is the best one to fit a data set, but little is known on the a priori possibility (in terms of number of data points or recording noise) to discriminate the binomial model against a simpler distribution.

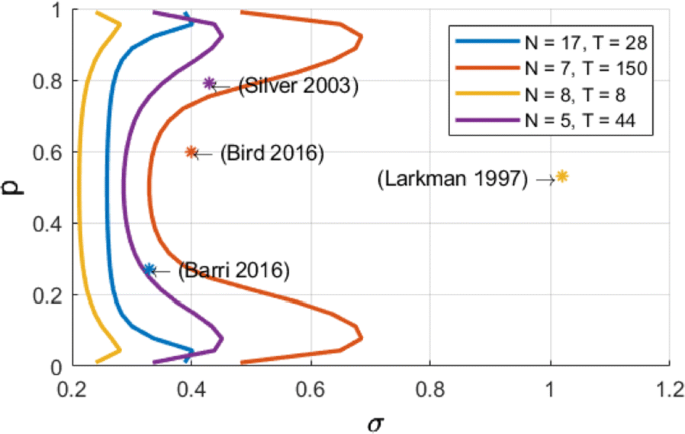
We compute an analytical identifiability domain for which the binomial model is correctly identified (Fig. 1), and we verify it by simulations. Our proposed methodology can be further extended and applied to other models of synaptic transmission, allowing to define and quantitatively assess a priori the experimental conditions to reliably fit the model parameters as well as to test hypotheses on the desired model compared to simpler versions.

In conclusion, our approach aims at providing experimentalists objectives for experimental design on the required number of data points and on the maximally acceptable recording noise. This approach allows to optimize experimental design, draw more robust conclusions on the validity of the parameter estimates, and correctly validate hypotheses on the binomial model.

References

1.
Katz B. The release of neural transmitter substances. Liverpool University Press (1969): 5–39.
2.
Barri A, Wang Y, Hansel D, Mongillo G. Quantifying repetitive transmission at chemical synapses: a generative-model approach. eNeuro 2016 Mar;3(2).
3.
Bird AD, Wall MJ, Richardson MJ. Bayesian inference of synaptic quantal parameters from correlated vesicle release. Frontiers in computational neuroscience 2016 Nov 25; 10:116.

O15 A flexible, fast and systematic method to obtain reduced compartmental models.

Willem Wybo, Walter Senn

University of Bern, Department of Physiology, Bern, Switzerland

Correspondence: Willem Wybo (willem.a.m.wybo@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O15

Most input signals received by neurons in the brain impinge on their dendritic trees. Before being transmitted downstream as action potential (AP) output, the dendritic tree performs a variety of computations on these signals that are vital to normal behavioural function [3, 8]. In most modelling studies however, dendrites are omitted due the cost associated with simulating them. Biophysical neuron models can contain thousands of compartments, rendering it infeasible to employ these models in meaningful computational tasks. Thus, to understand the role of dendritic computations in networks of neurons, it is necessary to simplify biophysical neuron models. Previous work has either explored advanced mathematical reduction techniques [6, 10] or has relied on ad-hoc simplifications to reduce compartment numbers [11]. Both of these approaches have inherent difficulties that prevent widespread adoption: advanced mathematical techniques cannot be implemented with standard simulation tools such as NEURON [2] or BRIAN [4], whereas ad-hoc methods are tailored to the problem at hand and generalize poorly. Here, we present an approach that overcomes both of these hurdles: First, our method simply outputs standard compartmental models (Fig 1A). The models can thus be simulated with standard tools. Second, our method is systematic, as the parameters of the reduced compartmental models are optimized with a linear least square fitting procedure to reproduce the impedance matrix of the biophysical model (Fig 1B). This matrix relates input current to voltage, and thus determines the response properties of the neuron [9]. By fitting a reduced model to this matrix, we obtain the response properties of the full model at a vastly reduced computational cost. Furthermore, since we are solving a linear least squares problem, the fitting procedure is well-defined—as there is a single minimum to the error function—and computationally efficient. Our method is not constrained to passive neuron models. By linearizing ion channels around wisely chosen sets of expansion points, we can extend the fitting procedure to yield appropriately rescaled maximal conductances for these ion channels (Fig 1C). With these conductances, voltage and spike output can be predicted accurately (Fig 1D, E). Since our reduced models reproduce the response properties of the biophysical models, non-linear synaptic currents, such as NMDA, are also integrated correctly. Our models thus reproduce dendritic NMDA spikes (Fig 1F). Our method is also flexible, as any dendritic computation (that can be implemented in a biophysical model) can be reproduced by choosing an appropriate set of locations on the morphology at which to fit the impedance matrix. Direction selectivity [1] for instance, can be implemented by fitting a reduced model to a set of locations distributed on a linear branch, whereas independent subunits [5] can be implemented by choosing locations on separate dendritic subtrees. In conclusion, we have created a flexible linear fitting method to reduce non-linear biophysical models. To streamline the process of obtaining these reduced compartmental models, work is underway on a toolbox (https://github.com/WillemWybo/NEAT) that automatizes the impedance matrix calculation and fitting process.

References

1.
Branco T, Clark B, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science Signaling 2010, Sept:1671–1675.
2.
Carnevale NT, Hines ML. The NEURON book 2004.
3.
Cichon J, Gan WB. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature 2015, 520(7546):180–185.
4.
Goodman DFM, Brette R. The Brian simulator. Frontiers in neuroscience 2009, 3(2):192– 7.
5.
Häusser M, Mel B. Dendrites: bug or feature? Current Opinion in Neurobiology 2003, 13(3):372–383.
6.
Kellems AR, Chaturantabut S, Sorensen DC, Cox SJ. Morphologically accurate reduced order modeling of spiking neurons. Journal of computational neuroscience 2010, 28(3):477–94.
7.
Koch C, Poggio T. A simple algorithm for solving the cable equation in dendritic trees of arbitrary geometry. Journal of neuroscience methods 1985, 12(4):303–315.
8.
Takahashi N, Oertner TG, Hegemann P, Larkum ME. Active cortical dendrites modulate perception. Science 2016, 354(6319):1587–90.
9.
Wybo WA, Torben-Nielsen B, Nevian T, Gewaltig MO. Electrical Compartmentalization in Neurons. Cell Reports 2019, 26(7):1759–1773.e7.
10.
Wybo WAM, Boccalini D, Torben-Nielsen B, Gewaltig MO. A Sparse Reformulation of the Green’s Function Formalism Allows Efficient Simulations of Morphological Neuron Models. Neural computation 2015, 27(12):2587–622.
11.
Traub RD, Pais I, Bibbig A, et al. Transient depression of excitatory synapses on interneurons contributes to epileptiform bursts during gamma oscillations in the mouse hippocampal slice. Journal of neurophysiology 2005 Aug;94(2):1225–35.

O16 An exact firing rate model reveals the differential effects of chemical versus electrical synapses in spiking networks

Ernest Montbrió¹, Alex Roxin², Federico Devalle¹, Bastian Pietras³, Andreas Daffertshofer³

¹Universitat Pompeu Fabra, Department of Information and Communication Technologies, Barcelona, Spain; ²Centre de Recerca Matemàtica, Barcelona, Spain; ³Vrije Universiteit Amsterdam, Behavioral and Movement Sciences, Amsterdam, Netherlands

Correspondence: Alex Roxin (aroxin@crm.cat)

BMC Neuroscience 2019, 20(Suppl 1):O16

Chemical and electrical synapses shape the collective dynamics of neuronal networks. Numerous theoretical studies have investigated how, separately, each of these types of synapses contributes to the generation of neuronal oscillations, but their combined effect is less understood. In part this is due to the impossibility of traditional neuronal firing rate models to include electrical synapses.

Here we perform a comparative analysis of the dynamics of heterogeneous populations of integrate-and-fire neurons with chemical, electrical, and both chemical and electrical coupling. In the thermodynamic limit, we show that the population’s mean-field dynamics is exactly described by a system of two ordinary differential equations for the center and the width of the distribution of membrane potentials —or, equivalently, for the population-mean membrane potential and firing rate. These firing rate equations exactly describe, in a unified framework, the collective dynamics of the ensemble of spiking neurons, and reveal that both chemical and electrical coupling are mediated by the population firing rate. Moreover, while chemical coupling shifts the center of the distribution of membrane potentials, electrical coupling tends to reduce the width of this distribution promoting the emergence of synchronization.

The firing rate equations are highly amenable to analysis, and allow us to obtain exact formulas for all the fixed points and their bifurcations. We find that the phase diagram for networks with instantaneous chemical synapses are characterized by a codimension-two Cusp point, and by the presence of persistent states for strong excitatory coupling. In contrast, phase diagrams for electrically coupled networks is determined by a Takens-Bogdanov codimension-two point, which entails the presence of oscillations and greatly reduces the presence of persistent states. Oscillations arise either via a Saddle-Node-Invariant-Circle bifurcation, or through a supercritical Hopf bifurcation. Near the Hopf bifurcation the frequency of the emerging oscillations coincides with the most likely firing frequency of the network. Only the presence of chemical coupling allows to shift (increase for excitation, and decrease for inhibition) the frequency of these oscillations. Finally, we show that the Takens-Bogdanov bifurcation scenario is generically present in networks with both chemical and electrical coupling.

Acknowledgement: We acknowledge support by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska Curie grant agreement No. 642563.

O17 Graph-filtered temporal dictionary learning for calcium imaging analysis

Gal Mishne¹, Benjamin Scott², Stephan Thiberge⁴, Nathan Cermak³, Jackie Schiller³, Carlos Brody⁴, David W. Tank⁴, Adam Charles⁴

¹Yale University, Applied Math, New Haven, CT, United States of America; ²Boston University, Boston, United States of America; ³Technion, Haifa, Israel; ⁴Princeton University, Department of Neuroscience, Princeton, NJ, United States of America

Correspondence: Gal Mishne (gal.mishne@yale.edu)

BMC Neuroscience 2019, 20(Suppl 1):O17

Optical calcium imaging is a versatile imaging modality that permits the recording of neural activity, including single dendrites and spines, deep neural populations using two-photon microscopy, and wide-field recordings of entire cortical surfaces. To utilize calcium imaging, the temporal fluorescence fluctuations of each component (e.g., spines, neurons or brain regions) must be extracted from the full video. Traditional segmentation methods used spatial information to extract regions of interest (ROIs), and then projected the data onto the ROIs to calculate the time-traces [1]. Current methods typically use a combination of both a-priori spatial and temporal statistics to isolate each fluorescing source in the data, along with the corresponding time-traces [2, 3]. Such methods often rely on strong spatial regularization and temporal priors that can bias time-trace estimation and that do not translate well across imaging scales.

We propose to instead model how the time-traces generate the data, using only weak spatial information to relate per-pixel generative models across a field-of-view. Our method, based on spatially-filtered Laplacian-scale mixture models [4,5], introduces a novel non-local spatial smoothing and additional regularization to the dictionary learning framework, where the learned dictionary consists of the fluorescing components’ time-traces.

We demonstrate on synthetic and real calcium imaging data at different scales that our solution has advantages regarding initialization, implicitly inferring number of neurons and simultaneously detecting different neuronal types (Fig. 1). For population data, we compare our method to a current state-of-the-art algorithm, Suite2p, on the publicly available Neurofinder dataset (Fig. 1C). The lack of strong spatial contiguity constraints allows our model to isolate both disconnected portions of the same neuron, as well as small components that would otherwise be over-shadowed by larger components. In the latter case, this is important as such configurations can easily cause false transients which can be scientifically misleading. On dendritic data our method isolates spines and dendritic firing modes (Fig. 1D). Finally, our method can partition widefield data [6] in to a small number of components that capture the scientifically relevant neural activity (Fig. 1E-F).

Acknowledgments: M is supported by NIH NIBIB and NINDS (grant R01EB026936).

References

1.
Mukamel EA, Nimmerjahn A, Schnitzer MJ. Automated analysis of cellular signals from large-scale calcium imaging data. Neuron 2009, 63, 747–760.
2.
Pachitariu M, et al. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv, 2016. 061507
3.
Pnevmatikakis EA, et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 2016, 89, 285–299.
4.
Garrigues P, Olshausen BA. Group sparse coding with a laplacian scale mixture prior. NIPS 2010, 676–684.
5.
Charles AS, Rozell CJ. Spectral superresolution of hyperspectral imagery using reweighted l1 spatial filtering. IEEE Geosci. Remote Sens. Lett. 2014, 11, 602–606.
6.
Scott BB, et al. Imaging Cortical Dynamics in GCaMP Transgenic Rats with a Head-Mounted Widefield Macroscope, Neuron 2018, 100, 1045–1058.

O18 Drift-resistant, real-time spike sorting based on anatomical similarity for high channel-count silicon probes

James Jun¹, Jeremy Magland¹, Catalin Mitelut², Alex Barnett¹

¹Flatiron Institute, Center for Computational Mathematics, New York, NJ, United States of America; ²Columbia University, Department of Statistics, New York, United States of America

Correspondence: James Jun (jjun@flatironinstitute.org)

BMC Neuroscience 2019, 20(Suppl 1):O18

Extracellular electrophysiology records a mixture of neural population activity at a single spike resolution. In order to resolve individual cellular activities, a spike-sorting operation groups together similar spike waveforms distributed at a subset of electrodes adjacent to each neuron. Penetrating micro-electrode arrays are widely used to measure the spiking activities from behaving animals, but silicon probes can be drifted in the brain due to animal movements or tissue relaxation following a probe penetration. The probe drift issue results in errors in conventional spike sorting operations that assumes stationarity in spike waveforms and amplitudes. Some of the latest silicon probes [1] offer a whole-shank coverage of closely-spaced electrode arrays, which can continually capture the spikes generated by neurons moving along the probe axis. We introduce a drift-resistant spike sorting algorithm for high channel-count, high-density silicon probe, which is designed to handle gradual and rapid random probe movements. IronClust takes advantage of the fact that a drifting probe revisits the same anatomical locations at various times. We apply a density-based clustering by grouping a temporal subset of the spiking events where the probe occupied similar anatomical locations. Anatomical similarities between a disjoint set of time bins are determined by calculating the activity histograms, which capture the spatial structures in the spike amplitude distribution based on the peak spike amplitudes on each electrode. For each spiking event, the clustering algorithm (DPCLUS [2]) computes the distances to a subset of its neighbors selected by their peak channel locations and the anatomical similarity. Based on the k-nearest neighbors [3], the clustering algorithm finds the density peaks based on the local density values and the nearest distances to the higher-density neighbors, and recursively propagates the cluster memberships toward a decreasing density gradient, The accuracy of our algorithm was evaluated using validation datasets generated using a biophysically detailed neural network simulator (BioNet [4]), which generated three scenarios including stationary, slow monotonic drift, and fast random drift cases. IronClust achieved ~8% error on the stationary dataset, and ~10% error on the gradual or random drift datasets, which significantly outperformed existing algorithms (Fig. 1). We also found that additional columns of electrodes improve the sorting accuracy in all cases. IronClust achieved over 11x of the real-time speed using GPU, and over twice faster than other leading algorithm. In conclusion, we realized an accurate and scalable spike sorting operation resistant to probe drift by taking advantage of an anatomically-aware clustering and parallel computing.

References

1.
Jun JJ et al. Fully integrated silicon probes for high-density recording of neural activity. Nature 2017 Nov;551(7679):232.
2.
Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science 2014 Jun 27;344(6191):1492–6.
3.
Rodriguez A, d’Errico M, Facco E, Laio A. Computing the free energy without collective variables. Journal of chemical theory and computation 2018 Feb 5;14(3):1206–15.
4.
Gratiy SL, et al. BioNet: A Python interface to NEURON for modeling large-scale networks. PloS one 2018 Aug 2;13(8):e0201630.

P1 Promoting community processes and actions to make neuroscience FAIR

Malin Sandström, Mathew Abrams

INCF, INCF Secretariat, Stockholm, Sweden

Correspondence: Malin Sandström (malin.sandstrom@incf.org)

BMC Neuroscience 2019, 20(Suppl 1):P1

The FAIR data principles were established as a general framework to facilitate knowledge discovery in research. Since the FAIR data principles are only guidelines, it is up to each domain to establish the standards and best practices (SBPs) that fulfill the principles. Thus, INCF is working with the community to develop, endorse, and adopt SBPs in neuroscience.

Develop: Connecting communities to support FAIR(er) practices

INCF provides 3 forums in which community members can come together to develop SBPs: Special Interest Groups (SIGs), Working Groups (WGs), and the INCF Assembly. SIGs are composed of a group of community members with the same interest, who gather and self-organize around tools, data, and community needs in a specific area. The SIGs will also serve as the focus for getting agreement and community buy-in on the use of these standards and best practices. INCF WGs are extensions of SIGs that receive funding from INCF to develop or extend existing SBPs, for example to support additional data types, or the development of a new SBP. The WG plan must include a plan for gathering appropriate input from the membership and the community. for example to support additional data types, or the development of a new SBP.

Endorse: Formalized standards endorsement process

The endorsement process is a continuous loop of feedback from the committee and the community to the developer(s) of the SBPs (e.g. PyNN and NeuroML [1,2]). Developers submit their SBPs for endorsement to the INCF SBP Committee who in turn vets the merit of the SBPs and publishes a report on the proposed standard covering openness, FAIRness, testing and implementation, governance, adoption and use, stability, and support. Then community is invited to comment during a 60-day period before the committee takes the final decision. Endorsed SBPs are then made available on incf.org and promoted to the community, to journals, and to funders through INCF’s training and outreach efforts.

Promote Adoption: Outreach and training

To promote adoption, INCF offers the yearly INCF Assembly where SIGs and WGs can present their work and engage the wider community. Training materials are also integrated into the INCF TrainingSpace, a platform linking world-class neuroinformatics training resources, developed by INCF in collaboration with its partners, and existing community resources. In addition to outreach and training, INCF also developed KnowledgeSpace, a community-based encyclopedia for neuroscience that links brain research concepts to the data, models, and literature that supports them, demonstrating how SBPs can facilitate linking brain research concepts with data, models and literature from around the world. It is an open project and welcomes participation and contributions from members of the global research community. KS is the result of recommendations from a community workshop held by the INCF Program on Ontologies of Neural Structures in 2012.

References

1.
Martone M, Das S, Goscinski W, et al. Call for community review of NeuroML — A Model Description Language for Computational Neuroscience [version 1; not peer reviewed] F1000Research 2019, 8:75 (document) (https://doi.org/10.7490/f1000research.1116398.1).
2.
Martone M, Das S, Goscinski W, et al. Call for community review of PyNN — A simulator-independent language for building neuronal network models [version 1; not peer reviewed]. F1000Research 2019, 8:74 (document) (https://doi.org/10.7490/f1000research.1116399.1).

P2 Ring integrator model of the head direction cells

Anu Aggarwal

Grand Valley State University, Electrical and Computer Engineering, Grand Rapids, MI, United States of America

Correspondence: Anu Aggarwal (aaagganu@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P2

Head direction (HD) cells have been demonstrated in the post subiculum [1, 2] of the hippocampal formation of the brain. Ensembles of the HD cells provide information about heading direction during spatial navigation. An Attractor Dynamic model [3] has been proposed to explain the unique firing patterns of the head direction cells. Here, we present a novel Ring Integrator model of the HD cells. This model is an improvement over the Attractor Dynamic model as it achieves the same functionality with fewer neurons and explains how the HD cells align to orienting cues.

References

1.
Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. Journal of Neuroscience 1990 Feb 1;10(2):420–35.
2.
Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. II. Effects of environmental manipulations. Journal of Neuroscience 1990 Feb 1;10(2):436–47.
3.
McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the ‘cognitive map’. Nature Reviews Neuroscience 2006 Aug;7(8):663.

P3 Parametric modulation of distractor filtering in visuospatial working memory.

Davd Bestue¹, Albert Compte², Torkel Klingberg³, Rita Almeida⁴

¹IDIBAPS, Barcelona, Spain; ²IDIBAPS, Systems Neuroscience, Barcelona, Spain; ³Karolinksa Institutet, Stockholm, Sweden; ⁴Stockholm University, Stockholm, Sweden

Correspondence: Davd Bestue (davidsanchezbestue@hotmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P3

Although distractor filtering has been long identified as a fundamental mechanism to achieve an efficient management of working memory, there are not many tasks where distractors are parametrically modulated both in the temporal and the similarity domain simultaneously. Here, 21 subjects participated in a visuospatial working memory task (vsWM) where distractors could be presented prospectively or retrospectively at two different delay times (200 and 7000 ms). Moreover, distractors were presented close or far away from the target. As expected, changes in the temporal and the similarity domain induced different distraction behaviours. In the similarity domain, we observed that close-by distractors induced an attractive bias while far distractors induced a repulsive one. Interestingly, this pattern of biases occurred both for prospective and retrospective distractors, suggesting common mechanisms of interference with the behaviorally relevant target. This result is in line with a previously validated bump-attractor model where diffusing bumps of neural activity attract or repel each other in the delay period [1]. In the temporal domain, we found a stronger effect for prospective distractors and short delays (200ms). Intriguingly, we observed that a retrospective distractor at 7000 ms also affected behavior, suggesting that irrelevant distractor memory traces can last longer than previously considered in computational models. One possibility is that persistent-activity based mechanisms underpin target storage while synaptic-based mechanisms underlie distractor memory traces. To gather support for this idea, we ran the same experiment with a 3T fMRI in 6 participants. Based on previous studies where sensory areas were not resistant to distractors [2], we hypothesized that sensory areas would represent all visual stimuli while associative areas like IPS would subserve memory-for-target function. Importantly, the synaptic hypothesis for distractor storage would predict that despite the behavioral evidence for retrospective distractor memory in this task, retrospective distractors would not be represented in the activity of either area, despite strong representations of the target. To test this, we will map parametric behavioral outputs into physiological activity readouts [3] for the different distractor conditions and we will explore the biological mechanism of distractor storage in working memory by comparing distractor storage in the retrospective 7000 ms condition with target storage in the absence of distractors. All together, these results open the door to an integrative model of working memory where different neural mechanisms and multiple brain regions are taken into account.

References

1.
Almeida R, Barbosa J, Compte A. Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study. Journal of Neurophysiology 2015 Jul 15;114(3):1806–18.
2.
Bettencourt KC, Xu Y. Decoding the content of visual short-term memory under distraction in occipital and parietal areas. Nature Neuroscience 2016 Jan;19(1):150.
3.
Ester EF, Sprague TC, Serences JT. Parietal and frontal cortex encode stimulus-specific mnemonic representations during visual working memory. Neuron 2015 Aug 19;87(4):893–905.

P4 Dynamical phase transitions study in simulations of finite neurons network

Cecilia Romaro¹, Fernando Najman², Morgan Andre²

¹University of São Paulo, Department of Physics, Ribeirão Preto, Brazil; ²University of São Paulo, Institute of Mathematics and Statistics, São Paulo, Brazil

Correspondence: Cecilia Romaro (cecilia.romaro@usp.br)

BMC Neuroscience 2019, 20(Suppl 1):P4

In [1], Ferrari et al. introduced a continuous time model for network of spiking neurons with binary membrane potential. It consists in an infinite system of interacting point processes. Each neuron in the one-dimensional lattice Z has two post-synaptic neurons, which are its two immediate neighbors. There is only two possible states for a given neuron, which are “active” or “quiescent” (1 or 0), and the neuron goes from “active” to “quiescent” either when it spikes, either when it is affected by the leakage effect, it goes from 0 to 1 when one of its presynaptic neurons spikes. For a given neuron the spikes are modeled as the events of a Poisson process of parameter 1, while the leakage events are modeled as the events of a Poisson process of some positive parameter gamma γ, all the processes being mutually independents. It was shown that this model presents a phase transition with respect to the parameter γ. This means that there exists a critical value for the parameter γ, denoted γc, such that, when γ>γc all neurons will once for all end up in the “quiescent” state with probability one; and when γ<γc there is a positive probability that the neurons will come back to the “active” state infinitely often.

However, when modeling the brain, it is usual to work with a necessarily finite number of neurons. Thus, we consider a finite version of the infinite system: instead of a process defined on entire lattice Z, we consider a version of the process defined on the finite window {−N, −N + 1, …, N − 1 N} (the number of neurons is therefore 2N + 1). When the number of neurons is finite we know by elementary results about Markov chains that the absorbent state, where all neurons are “quiescent”, will necessarily be reached in some finite time for any value of γ. The time t spent to reach the absorbent state depends on the network number of neuron 2N + 1 and the arbitrary parameter γ. For example, around 10⁷ random numbers were picked up until the network reached the absorbent state for N = 100 and γ = 0.375, but around 10⁹ random numbers were required when N was increased to 500 (Fig. 1).

So, we conjecture that, for a γ less than the critical gamma γc, the finite model presents a dynamical phase transition, as first defined in [2]. By this we mean that for a finite number of neurons, the distribution of the time of extinction (T(N,γ)) re-normalized (divided by its expectation) converges in distribution to an exponential random variable of parameter 1 when the number of neurons grows (N→∞). To back up our conjecture we build up the present model in python and run it 10,000 turns for N = (10, 50, 100, 500, 1000), J = (0.40, 0.35, 0.30) and plot the normalized histogram. The Fig. 1d shows the normalized histogram of the time of extinction for N = 50 (101 neurons) and J = 0.35 for 10,000 simulations and the function e-t in red.

Acknowledgements: This work was produced as part of the activities of FAPESP Research, Disseminations and Innovation Center for Neuromathematics (Grant 2013/07699-0, S. Paulo Research Foundation).

References

1.
Ferrari PA, Galves A, Grigorescu I, Löcherbach E. Phase transition for infinite systems of spiking neurons. Journal of Statistical Physics 2018 Sep 1;172(6):1564–75.
2.
Cassandro M, Galves A, Picco P. Dynamical phase transitions in disordered systems: the study of a random walk model. In Annales de l’IHP Physique théorique 1991 (Vol. 55, No. 2, pp. 689–705).

P5 Computational modeling of genetic contributions to excitability and neural coding in layer V pyramidal cells: applications to schizophrenia pathology

Tuomo Mäki-Marttunen¹, Gaute Einevoll², Anna Devor³, William A. Phillips⁴, Anders M. Dale³, Ole A. Andreassen⁵

¹Simula Research Laboratory, Oslo, Norway; ²Norwegian University of Life Sciences, Faculty of Science and Technology, Aas, Norway; ³University of California, San Diego, Department of Neurosciences, La Jolla, United States of America; ⁴University of Stirling, Psychology, Faculty of Natural Sciences, Stirling, United Kingdom; ⁵University of Oslo, NORMENT, KG Jebsen Centre for Psychosis Research, Division of Mental Health and Addiction, Oslo, Norway

Correspondence: Tuomo Mäki-Marttunen (tuomo@simula.no)

BMC Neuroscience 2019, 20(Suppl 1):P5

Layer V pyramidal cells (L5PCs) extend their apical dendrites throughout the cortical thickness of the neocortex and integrate information from local and distant sources [1]. Alterations in the L5PC excitability and its ability to process context- and sensory drive-dependent inputs have been proposed to be a cause for hallucinations and other impairments of sensory perceptions related to mental disease [2]. In line with this hypothesis, genetic variants in voltage-gated ion channel-encoding genes and their altered expression have been associated with the risk of mental disorders [4]. In this work, we use computational models of L5PCs to systematically study the impact of small-effect variants on L5PC excitability and phenotypes associated with schizophrenia (SCZ).

An important aid in SCZ research is the set of biomarkers and endophenotypes that reflect the impaired neurophysiology and—unlike most of the symptoms of the disorder—are translatable to animal models. The deficit in prepulse inhibition (PPI) is one of the most robust endophenotypes. Although statistical genetics and genome-wide association studies (GWASs) have helped to make associations between gene variants and disease phenotypes, the mechanisms of PPI deficits and other circuit dysfunctions related to SCZ are incompletely understood at the cellular level. Following our previous work [3], we here study the effects ofSCZ-associated genes on PPI in a single neuron.

In this work, we aim at bridging the gap of knowledge between SCZ genetics and disease phenotypes by using biophysically detailed models to uncover the influence of SCZ-associated genes on integration of information in L5PCs. L5PC population displays a wide diversity of morphological and electrophysiological behaviours, which has been overlooked in most modeling studies. To capture this variability, we use two separate models for thick-tufted L5PCs with partly overlapping ion-channel mechanisms and modes of input-output relationships. Furthermore, we generate alternative models that capture a continuum of firing properties between those attained by the two models. We show that most of the effects of SCZ-associated variants reported in [3] are robust across different types of L5PCs. Further, to generalize the results to in vivo-like conditions, we show that the effects of these model variants on single-L5PC excitability and integration of inputs persist when the model neuron is stimulated with noisy inputs. We also show that the model variants alter the way L5PCs code the input information both in terms of output action potentials and intracellular [Ca2+], which could contribute to both altered activity in the downstream neurons and synaptic long-term potentiation. Taken together, our results show a wide diversity in how SCZ-associated voltage-gated ion channel-encoding genes affect input-output relationships in L5PCs, and our framework helps to predict how these relationships are correlated with each other. These findings indicate that SCZ-associated variants may alter the interaction between perisomatic and apical dendritic regions.

References

1.
Hay E, Hill S, Schürmann F, Markram H, Segev I. Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Comput Biol 7, 7(2011): e1002107.
2.
Larkum M. A cellular mechanism for cortical associations: an organizing principle for the cerebral cortex. Trends in Neurosciences 36, 3(2013): 141–151.
3.
Mäki-Marttunen T, Halnes G, Devor A, et al. Functional effects of schizophrenia-linked genetic variants on intrinsic single-neuron excitability: a modeling study. Biol Psychiatry: Cogn Neurosci Neuroim 1, 1(2016): 49–59.
4.
Ripke S, Neale BM, Corvin A, Walters JT, et al. Biological insights from 108 schizophrenia-associated genetic loci. Nature 511, 7510(2014): 421.

P6 Spatiotemporal dynamics underlying successful cognitive therapy for posttraumatic stress disorder

Marina Charquero¹, Morten L Kringelbach¹, Birgit Kleim², Christian Ruff³, Steven C.R Williams⁴, Mark Woolrich⁵, Vidaurre Diego⁵, Ehlers Anke⁶

¹University of Oxford, Department of Psychiatry, Oxford, United Kingdom; ²University of Zurich, Psychotherapy and Psychosomatics, Zurich, Switzerland; ³University of Zurich, Zurich Center for Neuroeconomics (ZNE), Department of Economics, Zurich, Switzerland; ⁴King’s College London, Neuroimaging Department, London, United Kingdom; ⁵University of Oxford, Wellcome Trust Centre for Integrative NeuroImaging, Oxford Centre for Human Brain Activity (OHBA), Oxford, United Kingdom; ⁶University of Oxford, Oxford Centre for Anxiety Disorders and Trauma, Department of Experimental Psychology, Oxford, United Kingdom

Correspondence: Marina Charquero (marina.charqueroballester@psych.ox.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P6

Cognitive therapy for posttraumatic stress disorder (CT-PTSD) is one of the evidence-based psychological treatments. However, there are currently no fMRI studies investigating the temporal dynamics of brain network activation associated with successful cognitive therapy for PTSD. In this study, we used a newly developed data-driven approach to investigate the dynamics of brain function [1] underlying PTSD recovery with CT-PTSD [2].

Participants (43 PTSD, 30 remitted (14 pre & post CT-PTSD, 16 only post CT-PTSD), 8 waiting list and 15 healthy controls) underwent an fMRI protocol on a 1.5T Siemens Scanner using an echoplanar protocol (TR/TE 2400/40). The task consisted of trauma-related or neutral pictures presented in a semi-randomised block design. Data was preprocessed using FSL and FIX and nonlinearly registered to MNI space. Mean BOLD timeseries were estimated using the Shen functional atlas [3]. A Hidden Markov Model [1] was applied to estimate 7 states, each defined by a certain pattern of activation. The amount of total time spent in each network state (i.e., fractional occupancy) was computed separately for each of the two conditions: neutral and trauma-related pictures.

The states can be described as patterns of above- and below-average activation overlapping with functional (e.g., visual ventral stream) or resting-state networks (e.g., default mode network (DMN)). Results show that two DMN-related states, anatomically involving the medial temporal and the dorsomedial prefrontal DMN subsystems [4], had decreased fractional occupancies in PTSD in contrast to both healthy controls and remitted PTSD. No other states showed significant differences between groups. Importantly, there were no differences between PTSD before and after a waiting list condition (Fig 1). Furthermore, flashback qualities of intrusive memories were negatively related to the time spent in the medial temporal DMN as well as positively correlated with the time spent in ventral visual and salience states.

Recent work suggests that two subcomponents of the DMN, the medial temporal DMN and the dorsomedial prefrontal DMN, appear to be related to memory contextualisation and mentalizing about self and others, respectively [e.g. 4]. Our results show that the brains of participants with PTSD spend less time in states related to these two subcomponents before but not after successful therapy. This fits well with the cognitive theory suggested by [5], according to which PTSD results from: 1) disturbance of autobiographical memory characterised by poor contextualisation 2) excessively negative and threatening interpretations of one’s own and other people’s reactions to the trauma.

References

1.
Vidaurre D, Abeysuriya R, Becker R, et al. Discovering dynamic brain networks from big data in rest and task. Neuroimage 2018 Oct 15;180:646–56.
2.
Ehlers A, Clark DM, Hackmann A, McManus F, Fennell M. Cognitive therapy for post-traumatic stress disorder: development and evaluation. Behaviour research and therapy 2005 Apr 1;43(4):413–31.
3.
Shen X, Tokoglu F, Papademetris X, Constable RT. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage 2013 Nov 15;82:403–15.
4.
Andrews‐Hanna JR, Smallwood J, Spreng RN. The default network and self‐generated thought: component processes, dynamic control, and clinical relevance. Annals of the New York Academy of Sciences 2014 May 1;1316(1):29–52.
5.
Ehlers A, Clark DM. A cognitive model of posttraumatic stress disorder. Behaviour research and therapy 2000 Apr 1;38(4):319–45.

P7 Experiments and modeling of NMDA plateau potentials in cortical pyramidal neurons

Peng Gao¹, Joe Graham², Wen-Liang Zhou¹, Jinyoung Jang¹, Sergio Angulo², Salvador Dura-Bernal², Michael Hines³, William W Lytton², Srdjan Antic¹

¹University of Connecticut Health Center, Department of Neuroscience, Farmington, CT, United States of America; ²SUNY Downstate Medical Center, Department of Physiology and Pharmacology, Brooklyn, NY, United States of America; ³Yale University, Department of Neuroscience, CT, United States of America

Correspondence: Joe Graham (joe.w.graham@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P7

Experiments have shown that application of glutamate near basal dendrites of cortical pyramidal neurons activates AMPA and NMDA receptors, which can result in dendritic plateau potentials: long-lasting depolarizations which spread into the soma, reducing the membrane time constant and bringing the cell closer to the spiking threshold. Utilizing a morphologically-detailed reconstruction of a Layer 5 pyramidal cell from prefrontal cortex, a Hodgkin-Huxley compartmental model was developed in NEURON. Synaptic AMPA/NMDA and extrasynaptic NMDA receptor models were placed on basal dendrites to explore plateau potentials. The properties of the model were tuned to match plateau potentials recorded by voltage-sensitive dye imaging in dendrites and whole-cell patch measurements in somata of prefrontal cortex pyramidal neurons from rat brain slices. The model was capable of reproducing experimental observations: a threshold for activation of the plateau, saturation of plateau amplitude with increasing glutamate application, depolarization of the soma by approximately 20 mV, and back-propagating action potential amplitude attenuation and time delay. The model predicted that membrane time constant is shortened during the plateau, that synaptic inputs are more effective during the plateau due to both depolarization and time constant change, the plateau durations are longer when activated by more distal dendritic segments, and that plateau initiation location can be predicted from somatic plateau amplitude. Dendritic plateaus induced by strong basilar dendrite stimulation can increase population synchrony produced by weak coherent stimulation in apical dendrites. The morphologically-detailed cell model was simplified while maintaining the observed plateau behavior and then utilized in cortical network models along with a previously-published inhibitory interneuron model. The network model simulations showed increased synchrony between cells during induced dendritic plateaus. These results support our hypothesis that dendritic plateaus provide a 200-500 ms time window during which a neuron is particularly excitable. At the network level, this predicts that sets of cells with simultaneous plateaus would provide an activated ensemble of responsive cells with increased firing. Synchronously spiking subsets of these cells would then create an embedded ensemble. This embedded ensemble would demonstrate a temporal code, at the same time as the activated (embedded) ensemble showed rate coding.

P8 Systematic automated validation of detailed models of hippocampal neurons against electrophysiological data

Sára Sáray¹, Christian A Rössert², Andrew Davison³, Eilif Muller², Tamas Freund⁴, Szabolcs Kali⁴, Shailesh Appukuttan³

¹Faculty of Information Technology and Bionics, Pázmány Péter Catholic University, Hungary; ²École Polytechnique Fédérale de Lausanne, Blue Brain Project, Lausanne, Switzerland; ³Centre National de la Recherche Scientifique/Université Paris-Sud, Paris-Saclay Institute of Neuroscience, Gif-sur-Yvette, France; ⁴Institute of Experimental Medicine, Hungarian Academy of Sciences, Budapest, Hungary

Correspondence: Sára Sáray (saraysari@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P8

Developing biophysically and anatomically detailed data-driven computational models of the different neuronal cell types and running simulations on them is becoming a more and more popular method in the neuroscience community to investigate the behaviour and to understand or predict the function of these neurons in the brain. Several computational and software tools have been developed to build detailed neuronal models, and there is an increasing body of experimental data from electrophysiological measurements that describe the behavior of real cell neurons and thus constrain the parameters of detailed neuronal models. As a result, there are now a large number of different models of many cell types available in the literature.

These published models were usually built to capture some important or interesting properties of the given neuron type, i.e., to reproduce the results of a few selected experiments, and it is often unknown, even by their developers, how they would behave in other situations, outside their original context. Nevertheless, for data-driven models to be predictive, it is important that they are able to generalize beyond their original scope. Furthermore, investigating and developing different hippocampal CA1 pyramidal cell models we experienced that tuning the model parameters so that the model reproduces a specific behaviour often significantly changes previously adjusted behaviours, which can easily remain unrecognized by the modeler. This limits the reusability of these models for different scientific purposes. Therefore, it would be important to test and evaluate the models under different conditions, to explore the changes in model behaviour when its parameters are tuned.

To make it easier for the modeling community to explore the changes in model behavior during parameter tuning, and to systematically compare models of rat hippocampal CA1 pyramidal cells that were developed using different methods and for different purposes, we have developed an automated Python test suite called HippoUnit. HippoUnit is based on the SciUnit framework [1] which was developed for the validation of scientific models against experimental data. The tests of HippoUnit automatically run simulations on CA1 pyramidal cell models built in the NEURON simulator [2] that mimic the electrophysiological protocol from which the target experimental data were derived. Then the behavior of the model is evaluated and quantitatively compared to the experimental data using various feature-based error functions. Current validation tests cover somatic behavior and signal propagation and integration in apical dendrites of rat hippocampal CA1 pyramidal single cell models. The package is open source, available on GitHub (https://github.com/KaliLab/hippounit) and it has been integrated into the Validation Framework developed within the Human Brain Project.

Here we present how we applied HippoUnit to test and compare the behavior of several different hippocampal CA1 pyramidal cell models available on ModelDB [4], against electrophysiological data available in the literature. By providing the software tools and examples on how to validate these models, we hope to encourage the modeling community to use more systematic testing during model development, in order to create neural models that generalize better, and make the process of model building more reproducible and transparent.

References

1.
Omar C, Aldrich J, Gerkin RC. Collaborative infrastructure for test-driven scientific model validation. In Companion Proceedings of the 36th International Conference on Software Engineering 2014 May 31 (pp. 524–527). ACM.
2.
Carnevale NT, Hines M. The NEURON Book. Cambridge, UK: Cambridge University Press; 2006.
3.
Druckmann S, Banitt Y, Gidon AA, Schürmann F, Markram H, Segev I. A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Frontiers in neuroscience 2007 Oct 15;1:1.
4.
McDougal RA, Morse TM, Carnevale T, et al. Twenty years of ModelDB and beyond: building essential modeling tools for the future of neuroscience. Journal of computational neuroscience 2017 Feb 1;42(1):1–0.
5.
Appukuttan S, Garcia PE, Sharma BL, Sáray S, Káli S, Davison AP. Systematic Statistical Validation of Data-Driven Models in Neuroscience. Program No. 524.04. 2018 Neuroscience Meeting Planner San Diego, CA: Society for Neuroscience, 2018. Online.

P9 Systematic integration of experimental data in biologically realistic models of the mouse primary visual cortex: Insights and predictions

Yazan Billeh¹, Binghuang Cai², Sergey Gratiy¹, Kael Dai¹, Ramakrishnan Iyer¹, Nathan Gouwens¹, Reza Abbasi-Asl², Xiaoxuan Jia³, Joshua Siegle¹, Shawn Olsen¹, Christof Koch¹, Stefan Mihalas¹, Anton Arkhipov¹

¹Allen Institute for Brain Science, Modelling, Analysis and Theory, Seattle, WA, United States of America; ²Allen Institute for Brain Science, Seattle, WA, United States of America; ³Allen Institute for Brain Science, Neural Coding, Seattle, WA, United States of America

Correspondence: Yazan Billeh (yazanb@alleninstitute.org)

BMC Neuroscience 2019, 20(Suppl 1):P9

Data collection efforts in neuroscience are growing at an unprecedented pace, providing a constantly widening stream of highly complex information about circuit architectures and neural activity patterns. We leverage these data collection efforts to develop data-driven, biologically realistic models of the mouse primary visual cortex at two levels of granularity. The first model uses biophysically detailed neuron models with morphological reconstructions fit to experimental data. The second uses Generalized Leaky Integrate and Fire point neuron models fit to the same experimental recordings. Both models were developed using the Brain Modeling ToolKit (BMTK) and will be made freely available upon publication. We demonstrate how in the process of building these models, specific predictions about structure-function relationships in the mouse visual cortex emerge. We discuss three such predictions regarding connectivity between excitatory and non-parvalbumin expressing interneurons; functional specialization of connections between excitatory neurons; and the impact of the cortical retinotopic map on neuronal properties and connections.

P10 Small-world networks enhance the inter-brain synchronization

Kentaro Suzuki¹, Jihoon Park², Yuji Kawai², Minoru Asada²

¹Osaka University, Graduate School of Engineering, Minoh City, Japan; ²Osaka University, Suita, Osaka, Japan

Correspondence: Kentaro Suzuki (kentaro.suzuki@ams.eng.osaka-u.ac.jp)

BMC Neuroscience 2019, 20(Suppl 1):P10

Many hyperscanning studies have shown that activities of the two brains often synchronize during social interaction (e.g., [1]). This synchronization occurs in various frequency bands and brain regions [1]. Further, Dumas et al. [2] constructed a two-brain model in which Kuramoto oscillators, as brain regions, are connected according to an anatomically realistic human connectome. They showed that the model with the realistic brain structure exhibits stronger inter-brain synchronization than the network with a randomly shuffled structure. However, it remains unclear what properties in the brain anatomical structure contribute to the inter-brain synchronization. Furthermore, since Kuramoto oscillators tend to converge to a specific frequency, the model cannot explain the synchronous activities in different frequency bands which were observed in the hyperscanning studies. In the current study, we propose a two-brain model based on small-world networks proposed by Watts and Strogatz method (WS method) [3] to systematically investigate the relationship between the small-world structure and the degree of inter-brain synchronization. WS method can control the clustering coefficient and shortest path length without changing the number of connections by rewiring probability p (p = 0.0: regular network, p = 0.1: small-world network, and p = 1.0: random network). We hypothesize that the small-world network, which has high clustering coefficient and low shortest path length, is responsible for the inter-brain synchronization owing to its efficient information transmission. The model consists of two networks, each of which network consists of 100 neuron groups composed by 1000 spiking neurons (800 excitatory and 200 inhibitory neurons). The neuron groups in a network are connected according to WS method. Some groups in the two networks are directly connected as inter-brain connectivity, which is in the same manner as the previous model [2]. We evaluated the inter-brain synchronization between neuron groups using Phase Locking Value (PLV). Fig. 1 shows PLVs in each combination of networks with different rewiring probabilities in the gamma band (31-48Hz). The mean PLV of the combination of small-world networks was higher than those of the other combinations.

The result implies that the small-world structure in the brains may be a key factor of the inter-brain synchronization. As a future direction, we plan to impose an interaction task on the current model instead of the direct connections to aim to understand the relationship between the social interaction and structure properties of the brains.

Acknowledgments: This work was supported by JST CREST Grant Number JPMJCR17A4, and a project commissioned by the New Energy and Industrial Technology Development Organization (NEDO).

References

1.
Dumas G, Nadel J, Soussignan R, Martinerie J, Garnero L. Inter-brain synchronization during social interaction. PloS one 2010 Aug 17;5(8):e12166.
2.
Dumas G, Chavez M, Nadel J, Martinerie J. Anatomical connectivity influences both intra-and inter-brain synchronizations. PloS one 2012 May 10;7(5):e36414.
3.
Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature 1998 Jun;393(6684):440.

P11 A potential mechanism for phase shifts in grid cells: leveraging place cell remapping to introduce grid shifts

Zachary Sheldon¹, Ronald DiTullio², Vijay Balasubramanian²

¹University of Pennsylvania, Philadelphia, PA, United States of America; ²University of Pennsylvania, Computational Neuroscience Initiative, Philadelphia, United States of America

Correspondence: Zachary Sheldon (zsheldon@sas.upenn.edu)

BMC Neuroscience 2019, 20(Suppl 1):P11

Spatial navigation is a crucial part of survival, allowing an agent to effectively explore environments and obtain necessary resources. It has been theorized that this is achieved by learning an internal representation of space, known as a cognitive map. Multiple types of specialized neurons in the hippocampal formation and entorhinal cortex are believed to contribute to the formation of this cognitive map, particularly place cells and grid cells. These cells exhibit unique spatial firing fields that change in response to changes in environmental conditions. In particular, place cells display remapping of their spatial firing fields across different environments and grid cell display a phase shift in their spatial firing fields. If these cell types are indeed important for spatial navigation, we want to be able to explain the mechanism behind how the firing fields of these cell types change between environments. However, there are currently no suggested models or mechanisms for how this remapping and phase shift occur. Building off of previous work using continuous attractor network (CAN) models of grid cells, we propose a CAN model that incorporates place cell input to grid cells. By allowing for Hebbian learning between place cells and grid cells associated with two distinct environments, our model is able to replicate the phase shifts between environments observed in grid cells. Our model posits the first potential mechanism by which the cognitive map changes between environments, and will hopefully inspire new research into this phenomenon and spatial navigation as a whole.

P12 Computational modeling of seizure spread on a cortical surface explains the theta-alpha electrographic pattern

Viktor Sip¹, Viktor Jirsa¹, Maxime Guye², Fabrice Bartolomei³

¹Aix-Marseille Universite, Institute de Neurosciences, Marseille, France; ²Aix-Marseille Université, Centre de Résonance Magnétique Biologique et Médicale, Marseille, France; ³Assistance Publique - Hôpitaux de Marseille, Service de Neurophysiologie Clinique, Marseille, France

Correspondence: Viktor Sip (viktor.sip@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):P12

Intracranial electroencephalography is a standard tool in clinical evaluation of patients with focal epilepsy. Various early electrographic seizure patterns differing in frequency, amplitude, and waveform of the oscillations are observed in intracranial recordings. The pattern most common in the areas of seizure propagation is the so-called theta-alpha activity (TAA), whose defining features are oscillations in the theta-alpha range and gradually increasing amplitude. A deeper understanding of the mechanism underlying the generation of the TAA pattern is however lacking. We show by means of numerical simulation that the features of the TAA pattern observed on an implanted depth electrode in a specific epileptic patient can be plausibly explained by the seizure propagation across an individual folded cortical surface.

In order to demonstrate this, we employ following pipeline: First, the structural model of the brain is reconstructed from the T1-weighted images, and the position of the electrode contact are determined using the CT scan with implanted electrodes. Next, the patch of cortical surface in the vicinity of the electrode of interest is extracted. On this surface, the simulation of the seizure spread is performed using The Virtual Brain framework. As a mathematical model a field version of the Epileptor model is employed. The simulated source activity is then projected to the sensors using the dipole model, and this simulated stereo-electroencephalographic signal is compared with the recorded one.

The results show that the simulation on the patient-specific cortical surface gives a better fit between the recorded and simulated signals than the simulation on generic surrogate surfaces. Furthermore, the results indicate that the spectral content and dynamical features might differ in the source space of the cortical gray matter activity and among the intracranial sensors, questioning the previous approaches to classification of seizure onset patterns done in the sensor space, both based on spectral content and on dynamical features.

In conclusion, we demonstrate that the investigation of the seizure dynamics on the level of cortical surface can provide deeper insight into the large scale spatiotemporal organization of the seizure. At the same time, it highlights the need for a robust technique for inversion of the observed activity from sensor to source space that would take into account the complex geometry of the cortical sources and the position of the intracranial sensors.

References

1.
Perucca P, Dubeau F, Gotman J. Intracranial electroencephalographic seizure-onset patterns: effect of underlying pathology. Brain 2014, 137, 183–196.
2.
Sanz Leon P, Knock SA, Woodman MM, et al. The Virtual Brain: a simulator of primate brain network dynamics. Frontiers in Neuroinformatics 2013, Jun 11;7:10.
3.
Jirsa V, Stacey W, Quilichini P, Ivanov A, Bernard C. On the nature of seizure dynamics. Brain 2014, 137, 2110–2113.
4.
Proix T, Jirsa VK, Bartolomei F, Guye M, Truccolo W. Predicting the spatiotemporal diversity of seizure propagation and termination in human focal epilepsy. Nature Communications 2018, Mar 14;9(1):1088.

P13 Bistable firing patterns: one way to understand how epileptic seizures are triggered

Fernando Borges¹, Paulo Protachevicz², Ewandson Luiz Lameu³, Kelly Cristiane Iarosz⁴, Iberê Caldas⁴, Alexandre Kihara¹, Antonio Marcos Batista⁵

¹Federal University of ABC, Center for Mathematics, Computation, and Cognition., São Bernardo do Campo, Brazil; ²State University of Ponta Grossa, Graduate in Science Program, Ponta Grossa, Brazil; ³National Institute for Space Research (INPE), LAC, São José dos Campos, Brazil; ⁴University of São Paulo, Institute of Physics, São Paulo, Brazil; ⁵State University of Ponta Grossa, Program of Post-graduation in Science, Ponta Grossa, Brazil

Correspondence: Fernando Borges (fernandodasilvaborges@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P13

Excessively high, neural synchronisation has been associated with epileptic seizures, one of the most common brain diseases worldwide. Previous researchers have argued which epileptic and normal neuronal activity are support by the same physiological structure. However, to understand how neuronal systems transit between these regimes is a wide question to be answered. In this work, we study neuronal synchronisation in a random network where nodes are neurons with excitatory and inhibitory synapses, and neural activity for each node is provided by the adaptive exponential integrate-and-fire model. In this framework, we verify that the decrease in the influence of inhibition can generate synchronisation originating from a pattern of desynchronised spikes. The transition from desynchronous spikes to synchronous bursts of activity, induced by varying the synaptic coupling, emerges in a hysteresis loop due to bistability where abnormal (excessively high synchronous) regimes exist. We verify that, for parameters in the bistability regime, a square current pulse can trigger excessively high (abnormal) synchronisation, a process that can reproduce features of epileptic seizures. Then, we show that it is possible to suppress such abnormal synchronisation by applying a small-amplitude external current on less than 10% of the neurons in the network. Our results demonstrate that external electrical stimulation not only can trigger synchronous behaviour, but more importantly, it can be used as a means to reduce abnormal synchronisation and thus, control or treat effectively epileptic seizures.

P14 Can sleep protect memories from catastrophic forgetting?

Oscar Gonzalez¹, Yury Sokolov², Giri Krishnan², Maxim Bazhenov²

¹University of California, San Diego, Neurosciences, La Jolla, CA, United States of America; ²University of California, San Diego, Medicine, La Jolla, United States of America

Correspondence: Oscar Gonzalez (o2gonzalez@ucsd.edu)

BMC Neuroscience 2019, 20(Suppl 1):P14

Previously encoded memories can be damaged by encoding of new memories, especially when they are relevant to the new data and hence can be disrupted by new training—a phenomenon called “catastrophic forgetting”. Human and animal brains are capable of continual learning, allowing them to learn from past experience and to integrate newly acquired information with previously stored memories. A range of empirical data suggest important role of sleep in consolidation of recent memories and protection of the past knowledge from catastrophic forgetting. To explore potential mechanisms of how sleep can enable continual learning in neuronal networks, we developed a biophysically-realistic thalamocortical network model where we could train multiple memories with different degree of interference. We found that in a wake-like state of the model, training of a “new” memory that overlaps with previously stored “old” memory results in degradation of the old memory. Simulating NREM sleep state immediately after new learning led to replay of both old and new memories—this protected old memory from forgetting and ultimately enhanced both memories. The effect of sleep was similar to the interleaved training of the old and new memories. The study revealed that the network slow-wave oscillatory activity during simulated deep sleep leads to a complex reorganization of the synaptic connectivity matrix that maximizes separation between groups of synapses responsible for conflicting memories in the overlapping population of neurons. The study predicts that sleep may play a protective role against catastrophic forgetting and enables brain networks to undergo continual learning.

P15 Predicting the distribution of ion-channels in single neurons using compartmental models.

Roy Ben-Shalom¹, Kyung Geun Kim², Matthew Sit³, Henry Kyoung³, David Mao³, Kevin Bender¹

¹University of California, San-Francisco, Neurology, San-Francisco, CA, United States of America; ²University of California, Berkeley, EE/CS, Berkeley, CA, United States of America; ³University of California, Berkeley, Computer Science, Berkeley, United States of America

Correspondence: Roy Ben-Shalom (bens.roy@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P15

Neuronal activity arises from the concerted activity of different ionic currents that are distributed in varying densities across different neuronal compartments, including the axon, soma, and dendrite. One major challenge in understanding neuronal excitability remains understanding precisely how different ionic currents are distributed in neurons. Biophysically detailed neuronal compartmental models allow us to distribute the channels along the morphology of a neuron and simulate resultant voltage responses. One can then use optimization algorithms that fit model’s responses to the neuronal recordings to predict the channels distributions for the model. The quality of predictions generated from such models depends critically on the biophysical accuracy of the model. Depending on how optimization is implemented—both mathematically and experimentally—one can arrive at several solutions that all reasonably fit empirical datasets. However, to generate predictions that can be validated in experiments we need to reach a unique solution that predicts the neuronal activity for a rich repertoire of experimental conditions. As we increase the size of an empirical dataset, the number of model solutions that can accurately account for these empirical observations decreases, theoretically arriving at one unique solution. Here we present a novel approach designed to identify this unique solution in a multi-compartmental model by fitting models to data obtained from a somatic neuronal recording and post-hoc morphological reconstruction. To validate this approach, we began by reverse engineering a classic model of a neocortical pyramidal cell developed by [1], which contains 12 free parameters describing ion channels distributed across dendritic, somatic, and axonal compartments. First, we used the original values of these free parameters (e.g., the target data) to create a dataset of voltage responses that represents a ground truth. Given this target dataset, our goal was to determine whether we could use optimization to arrive at similar parameter values when these values were unknown. We tested over 350 different stimulation protocols and 15 score functions, which compare the simulated data to the ground truth dataset, to determine which combination of stimulation and score functions creates datasets that reliably constrain the model. Then we checked how sensitive each parameter was to different score functions. We found that five of the twelve parameters were sensitive to many different score functions. While these five could be constrained, the other seven parameters were sensitive only to a small set of score functions. We therefore divided the remaining optimization process to several steps, iteratively constraining a subset of the parameters that were sensitive to the same stimulation protocols and score functions. With this approach, were able to constrain 11/12 of the parameters of the model and recover the original values. This suggests that iterative, sensitivity analysis-based optimization could allow for more accurate fitting of model parameters to empirical data. We are currently testing whether similar methods can be used on more recently developed models with more free parameters. Ultimately, our goal is to apply this method to empirical recordings of neurons in acute slice and in vivo conditions.

Reference

1.
Mainen ZF, Sejnowski TJ. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 1996 Jul;382(6589):363.

P16 The contribution of dendritic spines to synaptic integration and plasticity in hippocampal pyramidal neurons

Luca Tar¹, Sára Sáray², Tamas Freund¹, Szabolcs Kali¹, Zsuzsanna Bengery²

¹Institute of Experimental Medicine, Hungarian Academy of Sciences, Budapest, Hungary; ²Faculty of Information Technology and Bionics, Pázmány Péter Catholic University, Hungary

Correspondence: Luca Tar (luca.tar04@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P16

The dendrites of cortical pyramidal cells bear spines which receive most of the excitatory synaptic input, act as separate electrical and biochemical compartments, and play important roles in signal integration and plasticity. In this study, we aimed to develop fully active models of hippocampal pyramidal neurons including spines to analyze the contributions of nonlinear processes in spines and dendrites to signal integration and synaptic plasticity. We also investigated ways to reduce the computational complexity of models of spiny neurons without altering their functional properties.

As a first step, we built anatomically and biophysically detailed models of CA1 pyramidal neurons without explicitly including dendritic spines. The models took into account multiple attributes of the cell determined by experiments, including the biophysics and distribution of ion channels, as well as the different electrophysiological characteristics of the soma and the dendrites. For systematic model development, we used two software tools developed in our lab: Optimizer [2] for automated parameter fitting, and the HippoUnit package, based on SciUnit [3] modules, to validate these results. We gradually increased the complexity of our model, mainly by adding further types of ion channels, and monitored the ability of the model to capture both optimized and non-optimized features and behaviors. This method allowed us to determine the minimal set of mechanisms required to replicate particular neuronal behaviors and resulted in a new model of CA1 pyramidal neurons whose characteristics match a wide range of experimental results.

Next, starting from a model which matched the available data on nonlinear dendritic integration [5], we added dendritic spines and moved excitatory synapses to the spine head. Simply adding the spines to the original model significantly changed the propagation of signals in dendrites, the properties of dendritic spikes and the overall characteristics of synaptic integration. This was due mainly to the effective change in membrane capacitance and the density of voltage-gated and leak conductances, and could be compensated by appropriate changes in these parameters. The resulting model showed the correct behavior for nonlinear dendritic integration while explicitly implementing all dendritic spines.

As the effects of spines on dendritic spikes and signal propagation could be largely explained by their effect on the membrane capacitance and conductance, we also developed a simplified version of the model where only those dendritic spines which received synaptic input were explicitly modeled, while the rest of the spines were implicitly taken into account by appropriate changes in the membrane properties. This model behaved very similarly to the one where all spines were explicitly modeled, but ran significantly faster. Our approach generalizes the F-factor method of [4] to active models.

Finally, our models which show realistic electrical behavior in their dendrites and spines allow us to examine Ca dynamics in dendritic spines in response to any combination of synaptic inputs and somatic action potentials. In combination with models of the critical molecular signaling pathways [1], this approach enables a comprehensive computational investigation of the mechanisms underlying activity-dependent synaptic plasticity in hippocampal pyramidal neurons.

References

1.
Lindroos R, Dorst MC, Du K, et al. Basal Ganglia Neuromodulation Over Multiple Temporal and Structural Scales—Simulations of Direct Pathway MSNs Investigate the Fast Onset of Dopaminergic Effects and Predict the Role of Kv4. 2. Frontiers in neural circuits 2018 Feb 6;12:3.
2.
Friedrich P, Vella M, Gulyás AI, Freund TF, Káli S. A flexible, interactive software tool for fitting the parameters of neuronal models. Frontiers in neuroinformatics 2014 Jul 10;8:63.
3.
Omar C, Aldrich J, Gerkin RC. Collaborative infrastructure for test-driven scientific model validation. In Companion Proceedings of the 36th International Conference on Software Engineering 2014 May 31 (pp. 524–527). ACM.
4.
Rapp M, Yarom Y, Segev I. The impact of parallel fiber background activity on the cable properties of cerebellar Purkinje cells. Neural Computation 1992 Jul;4(4):518–33.
5.
Losonczy A, Magee JC. Integrative properties of radial oblique dendrites in hippocampal CA1 pyramidal neurons. Neuron 2006 Apr 20;50(2):291–307.

P17 Modelling the dynamics of optogenetic stimulation at the whole-brain level

Giovanni Rabuffo¹, Viktor Jirsa¹, Francesca Melozzi¹, Christophe Bernard¹

¹Aix-Marseille Université, Institut de Neurosciences des Systèmes, Marseille, France

Correspondence: Giovanni Rabuffo (giovanni.rabuffo@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):P17

Deep brain stimulation is commonly used in different pathological conditions, such as Parkinson’s disease, epilepsy, and depression. However, there is scant knowledge regarding the way of stimulating the brain to cause a predictable and beneficial effect. In particular, the choice of the area to stimulate and the stimulation settings (amplitude, frequency, duration) remain empirical [1].

To approach these questions in a theoretical framework, an understanding of how stimulation propagates and influences the global brain dynamics is of primary importance.

A precise stimulation (activation/inactivation) of specific cell-types in brain regions of interest can be obtained using optogenetic methods. Such stimulation will act in a short-range domain i.e., local in the brain region, as well as on a large-scale network. Both these effects are important to understand the final outcome of the stimulation [2]. Therefore, a whole brain approach is required.

In our work we use The Virtual Brain platform to model an optogenetic stimulus and to study its global effects on a “virtual” mouse brain [3]. The parameters of our model can be gauged in order to account for the intensity of the stimulus, which is generally controllable during experimental tests.

The functional activity of the mouse brain model can be compared to experimental evidences coming from in vivo optogenetic fMRI (ofMRI) [4]. In silico exploration of the parameter space allows then to fit the results of an ofMRI dataset as well as to make predictions on the outcome of a stimulus depending not only by its anatomical location and cell-type, but also by the connection topology.

The theoretical study of the network dynamics emerging from such adjustable and traceable stimuli, provides a step forward in the understanding of the causal relation between structural and functional connectomes.

References

1.
Sironi VA. Origin and evolution of deep brain stimulation. Frontiers in integrative neuroscience 2011 Aug 18;5:42.
2.
Fox MD, Buckner RL, Liu H, Chakravarty MM, Lozano AM, Pascual-Leone A. Resting-state networks link invasive and noninvasive brain stimulation across diverse psychiatric and neurological diseases. Proceedings of the National Academy of Sciences 2014 Oct 14;111(41):E4367–75.
3.
Melozzi F, Woodman MM, Jirsa VK, Bernard C. The virtual mouse brain: a computational neuroinformatics platform to study whole mouse brain dynamics. eNeuro 2017 May;4(3).
4.
Lee JH, Durand R, Gradinaru V, et al. Global and local fMRI signals driven by neurons defined optogenetically by type and wiring. Nature 2010 Jun;465(7299):788.

P18 Investigating the effect of the nanoscale architecture of astrocytic processes on the propagation of calcium signals

Audrey Denizot¹, Misa Arizono², Weiliang Chen³, Iain Hepburn³, Hédi Soula⁴, U. Valentin Nägerl², Erik De Schutter³, Hugues Berry⁵

¹INSA Lyon, Villeurbanne, France; ²Université de Bordeaux, Interdisciplinary Institute for Neuroscience, Bordeaux, France; ³Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Onna-Son, Japan; ⁴University of Pierre and Marie Curie, INSERM UMRS 1138, Paris, France; ⁵INRIA, Lyon, France

Correspondence: Audrey Denizot (audrey.denizot@inria.fr)

BMC Neuroscience 2019, 20(Suppl 1):P18

According to the concept of the ‘tripartite synapse’ [1], information processing in the brain results from dynamic communication between pre- and post- synaptic neurons and astrocytes. Astrocyte excitability results from transients of cytosolic calcium concentration. Local calcium signals are observed both spontaneously and in response to neuronal activity within fine astrocyte ramifications [2, 3], that are in close contact with synapses [4]. Those fine processes, that belong to the so-called spongiform structure of astrocytes, are too fine to be resolved spatially with conventional light microscopy [5, 6]. However, calcium dynamics in these structures can be investigated by computational modeling. In this study, we investigate the roles of the spatial properties of astrocytic processes on their calcium dynamics. Because of the low volumes and low number of molecules at stake, we use our stochastic spatially-explicit individual-based model of astrocytic calcium signals in 3D [7], implemented with STEPS [8]. We validate our model by reproducing key parameters of calcium signals that we have recorded with high-resolution calcium imaging in organotypic brain slices. Our simulations reveal the importance of the spatial organization of the implicated molecular actors for calcium dynamics. Particularly, we predict that different spatial organizations can lead to very different types of calcium signals, even for two processes displaying the exact same calcium channels, with the same densities. We also investigate the impact of process geometry at the nanoscale on calcium signal propagation. By modeling realistic astrocyte geometry at the nanoscale, this study thus proposes plausible mechanisms for information processing within astrocytes as well as neuron-astrocyte communication.

References

1.
Araque A, Parpura V, Sanzgiri RP, Haydon PG. Tripartite synapses: glia, the unacknowledged partner. Trends in neurosciences 1999 May 1;22(5):208–15.
2.
Arizono M, et al. Structural Basis of Astrocytic Ca2+ Signals at Tripartite Synapses. Social Science Research Network 2018.
3.
Bindocci E, Savtchouk I, Liaudet N, Becker D, Carriero G, Volterra A. Three-dimensional Ca2+ imaging advances understanding of astrocyte biology. Science 2017 May 19;356(6339):eaai8185.
4.
Ventura R, Harris KM. Three-Dimensional Relationships between Hippocampal Synapses and Astrocytes. Journal of Neuroscience 1999, Aug 15;19(16): 6897–6906.
5.
Heller JP, Rusakov DA. The nanoworld of the tripartite synapse: insights from super-resolution microscopy. Frontiers in Cellular Neuroscience 2017 Nov 24;11:374.
6.
Panatier A, Arizono M, Nägerl UV. Dissecting tripartite synapses with STED microscopy. Phil Trans of the Royal Society B: Biological Sciences 2014 Oct 19;369(1654):20130597.
7.
Audrey D, Misa A, Valentin NU, Hédi S, Hugues B. Simulation of calcium signaling in fine astrocytic processes: effect of spatial properties on spontaneous activity. bioRxiv 2019 Jan 1:567388.
8.
Hepburn I, Chen W, Wils S, De Schutter E. STEPS: efficient simulation of stochastic reaction–diffusion models in realistic morphologies. BMC systems biology 2012 Dec;6(1):36.

P19 Neural mass modeling of the Ponto-Geniculo-Occipital wave and its neuromodulation

Kaidi Shao¹, Nikos Logothetis¹, Michel Besserve¹

¹MPI for Biological Cybernetics, Department for Physiology of Cognitive Processes, Tübingen, Germany

Correspondence: Kaidi Shao (kdshao@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P19

As a prominent feature of Rapid Eye Movement (REM) sleep and the transitional stage from Slow Wave Sleep to REM sleep (the pre-REM stage), Ponto-Geniculo-Occipital (PGO) waves are hypothesized to play a critical role in dreaming and memory consolidation [1]. During pre-REM and REM stages, PGO waves appear in two subtypes differing in number, amplitude and frequency. However, the mechanisms underlying their generation and propagation across multiple brain structures, as well as their functions, remains largely unexplored. In particular, contrary to the multiple phasic events occurring during non-REM sleep (slow waves, spindles and sharp-wave ripples), computational modeling of PGO waves has to the best of our knowledge not yet been investigated.

Based on experimental evidence in cats, the species were most extensively studied, we elaborated an existing thalamocortical model operating in the pre-REM stage [2], and constructed a ponto-thalamo-cortical neural mass model consisting of 6 rate-coded neuronal populations interconnected via biologically-verified synapses (Fig. 1A). Transient PGO-related activities are elicited by a single or multiple brief pulses, modelling the input bursts that PGO-triggering neurons send to cholinergic neurons in the pedunculopontine tegmentum nucleus (PPT). The effect of acetylcholine (ACh), as the primarily-affecting neuromodulator during the SWS-to-REM transition, was also modelled by tuning several critical parameters with tonically-varying ACh concentration.

Our simulations are able to reproduce deflections in local field potentials (LFPs), as well as other electrophysiological characteristics consistent in many respects with classical electrophysiological studies (Fig. 1B). For example, the duration of both subtypes of thalamic PGO waves matches that of the PGO recordings with a similar waveform comprised of a sharp negative peak and a slower positive peak. The bursting duration of TC and RT neurons (10ms, 25ms) falls in the range reported by experimental papers (7-15ms, 20-40ms). Consistent with experimental findings, the simulated PGO waves block spindle oscillations that occur during pre-REM stage. By incorporating tonic cholinergic neuromodulation to mimic the SWS-to-REM transition, we were also able to replicate the electrophysiological differences between the two PGO subtypes with an ACh-tuned leaky potassium conductance in TC and RT neurons (Fig. 1C).

These results help clarify the cellular mechanisms underlying thalamic PGO wave generation, e.g., the nicotinic depolarization of LGin neurons, whose role used to be under debate, is shown to be critical for the generation of the negative peak. The model elucidates how ACh modulates state transitions throughout the wake-sleep cycle, and how this modulation leads to a recently-reported difference of transient change in the thalamic multi-unit activities. The simulated PGO waves also provides us a biologically-plausible framework to investigate how they take part in the multifaceted brain-wide network phenomena occurring during sleep and the enduring effects they may induce through plasticity.

References

1.
Gott JA, Liley DT, Hobson JA. Towards a functional understanding of PGO waves. Frontiers in human Neuroscience 2017 Mar 3;11:89.
2.
Costa MS, Weigenand A, Ngo HV, et al. A thalamocortical neural mass model of the EEG during NREM Sleep and its response to auditory stimulation. PLoS computational biology 2016 Sep 1;12(9):e1005022.

P20 Oscillations in working memory and neural binding: a mechanism for multiple memories and their interactions

Jason Pina¹, G. Bard Ermentrout², Mark Bodner³

¹York University, Physicsand Astronomy, Toronto, Canada; ²University of Pittsburgh, Department of Mathematics, Pittsburgh, PA, United States of America; ³Mind Research Institute, Irvine, United States of America

Correspondence: Jason Pina (jay.e.pina@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P20

Working memory is a form of short term memory that seems to be limited in capacity to 3–5 items. It is well known that neurons increase their firing rates from a low baseline state while information is being retained during working memory tasks. However, there is evidence of oscillatory firing rates in the active states, both in individual and in aggregate (for example, LFP and EEG) dynamics. Additionally, each memory may be composed of several different items, such as shape, color, and location. The neural correlate of the association of several items, or neural binding, is not well understood, but may be the synchronous firing of populations of neurons. Thus, the phase information of such oscillatory ensemble activity is a natural candidate to distinguish between bound (synchronous oscillations) and distinct (out-of-phase oscillations) items held actively in working memory.

Here, we explore a population firing rate model that exhibits bistability between a low baseline firing rate and a high, oscillatory firing rate. Coupling several of these populations together to form a firing rate network allows for competitive oscillatory dynamics, whereby different populations may be pairwise synchronous or out-of-phase, corresponding to bound or distinct items in memory, respectively. We find that up to 3 populations may oscillate out-of-phase with plausible modelconnectivitiesand parameter values, a result that is consistent with working memory capacity. The formulation of the model allows us to better examine from a dynamical systems perspective how these states arise as bifurcations of steady states and periodic orbits. In particular, we look at the ranges of coupling strengths and synaptic time scales that allow for synchronous and out-of-phase attracting states. We also explore how varying patterns of selective stimuli can produce and switch between rich sets of dynamics that may be relevant to working memory states and their transitions.

P21 DeNSE: modeling neuronal morphology and network structure in silico

Tanguy Fardet¹, Alessio Quaresima², Samuel Bottani²

¹University of Tübingen, Computer Science Department - Max Planck Institute for Biological Cybernetics, Tübingen, Germany; ²Université Paris Diderot, Laboratoire Matière et Systèmes Complexes, Paris, France

Correspondence: Tanguy Fardet (tanguy.fardet@tuebingen.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):P21

Neural systems develop and self-organize into complex networks which can generate stimulus-specific responses. Neurons grow into various morphologies, which influences their activity and the structure of the resulting network. Different network topologies can then display very different behaviors, which suggests that neuronal structure and network connectivity strongly influence the set of functions that can be sustained by a set of neurons. To investigate this, I developed a new simulation platform, DeNSE, aimed at studying the morphogenesis of neurons and networks, and enabling to test how interactions between neurons and their surroundings can shape the emergence of specific properties.

The goal of this new simulator is to serve as a general framework to study the dynamics of neuronal morphogenesis, providing predictive tools to investigate how neuronal structures emerge in complex spatial environments. The software generalizes models present in previous simulators [1, 2], gives access to new mechanisms, and accounts for spatial constraints and neuron-neuron interactions. It has been primarily applied on two main lines of research: a) neuronal cultures or devices, their structures being still poorly defined and strongly influenced by interactions or spatial constraints [3], b) morphological determinants of neuronal disorders, analyzing how changes at the cellular scale affect the properties of the whole network [4].

I illustrate how DeNSE enables to investigate neuronal morphology at different scales, from single cell to network level, notably through cell-cell and cell-surroundings interactions (Fig. 1). At the cellular level, I show how branching mechanisms affect neuronal morphology, introducing new models to account for interstitial branching and the influence of the environment. At intermediate levels, I show how DeNSE can reproduce interactions between neurites and how these contribute to the final morphology and introduce correlations in the network structure. At the network level, I stress how networks obtained through a growth process differ from both simple generative models and more complex network models where the connectivity comes from overlaps of real cell morphologies. Eventually, I demonstrate how DeNSE can provide biologically relevant structures to study spatio-temporal activity patterns in neuronal cultures and devices. In these structures, where the morphologies of the neurons and the network are not well defined but have been shown to play a significant role, DeNSE successfully reproduces experimental setups, predicts the influence of spatial constraints, and enables to predict their electrical activities. Such a tool can therefore be extremely useful to test structures and hypotheses prior to actual experiments, thus saving time and resources.

References

1.
Koene, R et al. NETMORPH: a framework for the stochastic generation of large-scale neuronal networks with realistic neuron morphologies. Neuroinformatics 2009, 7(3), 195–210
2.
Torben-Nielsen, B et al. Context-aware modeling of neuronal morphologies. Frontiers in Neuroanatomy 2014, 8(92)
3.
Renault, R et al. Asymmetric axonal edge guidance: a new paradigm for building oriented neuronal networks. Lab Chip 2016, 16(12), 2188–2191
4.
Milatovic D et al. Morphometric Analysis in Neurodegenerative Disorder. Current Protocols in Toxicology 2010, Feb 1;43(1):12–6.

P22 Sponge astrocyte model: volume effects in a 2D model space simplification

Darya Verveyko¹, Andrey Verisokin¹, Dmitry Postnov², Alexey R. Brazhe³

¹Kursk State University, Department of Theoretical Physics, Kursk, Russia; ²Saratov State University, Institute for Physics, Saratov, Russia; ³Lomonosov Moscow State University, Department of Biophysics, Moscow, Russia

Correspondence: Darya Verveyko (allegroform@mail.ru)

BMC Neuroscience 2019, 20(Suppl 1):P22

Calcium signaling in astrocytes is crucial for the nervous system function. Earlier we proposed a 2Dastrocytemodelof calcium waves dynamics [1], where waves were driven by local stochastic surges of glutamate which simulated the synaptic activity. The main idea of the model was in reproducing the spatially segregated mechanisms, belonging to regions with different dynamics: (i) the core with calcium exchange mainly with endoplasmic reticulum (ER) and (ii) peripheral compartment with currents through a plasma membrane (PM) with dominating Ca dynamics.

Real astrocytes are obviously not binary. There is a graded transition from thick branches to branchlets and to leaflets, primarily determined via the surface-to-volume ratio (SVR). Moreover, leaflet regions of the template contain not only astrocyte itself, but also the neuropil. We encode the astrocyte structural features by means of its color representation. Let the black color corresponds to astrocyte-free region, and the blue channel color indicate the presence of an astrocyte. Instead of binary leaflet-branch segregation, we introduce the astrocyte volume fraction (AVF) parameter, which indicates how much of the 2D cell volume is occupied by the astrocyte in real 3D effigy (the rest part is neuropil). AVF is encoded by the red channel intensity (Fig. 1A). The soma and thick branches region contain only the astrocyte (AVF = 1). The non-astro content increases from the soma to edges of an astrocyte through the leaflets, so AVF parameter should decrease and the red channel tends to its minimum value equal to 0.1 on the astrocyte border. To describe the relative effect of the exchange through PM and ER, we introduce the SVR parameter, which depends on AVF as a reverse sigmoid form. The SVR value is maximal at the edges of the leaflets and minimal in the soma.

The implementation of AVF and SVR effects is based on the following reasoning: larger AVF (correspondingly, smaller SVR) reflects Ca dynamics dominated by ER exchange (IP3R-mediated) and less input from PM mechanisms (IP3 synthesis and PM-mediated Ca currents). Larger SVR in turn reflects underlying tortuosity of the astrocyte cytoplasm volume by attenuating apparent diffusion coefficients for IP3 and Ca. Finally, small concentration changes in areas with high AVF will cause larger changes in concentration in the neighboring areas with low AVF due to unequal volumes taken up by astrocytic cytoplasm.

Simulations of the proposed model show the formation of calcium waves (Fig. 1B), which propagate throughout the astrocyte template from the borders towards the center. In contrast to the previous binary segmentation model, calcium elevation response in the proposed biophysically more realistic sponge model is greater, i.e. the intensity of the formed waves is higher, but the basal calcium level is lower (Fig. 1C). At the same time, the threshold of stable wave existence grows because increasing AVF works like a blocking barrier for a small glutamate release reducing the number of wave sources. Nevertheless, large enough glutamate release leads to a wide-area wave quickly occupying the leaflets moving to the astrocyte soma.

Acknowledgements: This work is supported by the RFBR grant 17-00-00407.

Reference

1.
Verveyko DV, et al. Raindrops of synaptic noise on dual excitability landscape: an approach to astrocyte network modelling. Proceedings SPIE 2018, 10717, 107171S.

P23 Sodium-calcium exchangers modulate excitability of spatially distributed astrocyte networks

Andrey Verisokin¹, Darya Verveyko¹, Dmitry Postnov², Alexey R. Brazhe³

¹Kursk State University, Department of Theoretical Physics, Kursk, Russia; ²Saratov State University, Institute for Physics, Saratov, Russia; ³Lomonosov Moscow State University, Department of Biophysics, Moscow, Russia

Correspondence: Andrey Verisokin (ffalconn@mail.ru)

BMC Neuroscience 2019, 20(Suppl 1):P23

Previously we proposed two models of astrocytic calcium dynamics modulated by local synaptic activity. The first one [1] is based on the inositol trisphosphate-dependent exchange with the intracellular calcium storage taking into account specific topological features, namely different properties of thick branches and soma with thin branches. The second local model for a separate segment of an astrocyte [2] considers the sodium-calcium exchanger (NCX) and Na+ response to the synaptic glutamate. In this work we combine these two models and proceed to a spatially distributed astrocyte network. Our main goal is to study the process of the cytoplasmic calcium wave initiation and its motion through the astrocyte network.

The astrocyte cell is represented in the model by a 2D projection of a real cell microphotograph and indicated by a blue colour. The intensity of a red channel in each pixel shows the cytoplasm/ neuropil volume ratio. We introduce this volume characteristic to describe the differences in diffusion rates and the contribution of ion currents through endoplasmic reticulum membrane and plasma membrane in soma, branches and leaflets. We further connect various astrocyte cell templates into a network (Fig. 1A).

The proposed mathematical model includes 7 variables: calcium concentrations in cytosol andendoplasmic reticulum, inositol trisphosphate and sodium concentrations incytosol, extracellular glutamate concentration, inositol trisphosphatereceptor and NCX inactivation gating variables h and g. Synaptic glutamate activity is described by a quantal release triggered by a spike train drawn from a homogeneous Poisson process. A detailed description of the model equations and parameters including its biophysical meaning is provided in [1, 2].

The results of the unified model numerical solution confirm the emergence of calcium waves, which occur due to the synaptic activity and spread over the astrocyte network (Fig. 1B). Depending on the excitation level and the network topology, the combination of two possible scenarios is forming: calcium excitation wave captures the entire astrocyte network, along with local waves, which exist only within one cell and terminate beyond its borders. The first scenario includes the regime when one of the cells acts as a pacemaker, i.e. the source of periodic calcium waves (Fig. 1C). The statistics on area and duration of calcium excitation events in the case of the presence and absence of NCX regulations was obtained using complementary cumulative distribution functions (CCDF). The presence of NCX leads to a decrease in the average areas that are affected by a global calcium wave during excitation, while the number of events with equal duration time is the same on average for both models (Fig. 1D). However, the Na/Ca-exchanger stimulates calcium waves, making possible the formation of more long-lived waves.

Acknowledgements: This study was supported by Russian Science Foundation, grant 17-74-20089.

References

1.
Verveyko DV, et al. Raindrops of synaptic noise on dual excitability landscape: an approach to astrocyte network modelling. Proceedings SPIE 2018, 10717, 107171S.
2.
Brazhe AR, et al. Sodium–calcium exchanger can account for regenerative Ca2+ entry in thin astrocyte processes. Frontiers in Cellular Neuroscience 2018, 12, 250.

P24 Building a computational model of aging in visual cortex

Seth Talyansky¹, Braden Brinkman²

¹Catlin Gabel School, Portland, OR, United States of America; ²Stony Brook University, Department of Neurobiology and Behavior, Stony Brook, NY, United States of America

Correspondence: Seth Talyansky (talyanskys@catlin.edu)

BMC Neuroscience 2019, 20(Suppl 1):P24

The mammalian visual system has been the focus of countless experimental and theoretical studies designed to elucidate principles of sensory coding. Most theoretical work has focused on networks intended to reflect developing or mature neural circuitry, in both health and disease. Few computational studies have attempted to model changes that occur in neural circuitry as an organism ages non-pathologically. In this work we begin to close this gap, studying how physiological changes correlated with advanced age impact the computational performance of a spiking network model of primary visual cortex (V1).

Senescent brain tissue has been found to show increased excitability [1], decreased GABAergic inhibition [2], and decreased selectivity to the orientation of grating stimuli [1]. While the underlying processes driving these changes with age are far from clear, we find that these observations can be replicated by a straightforward, biologically-interpretable modification to a spiking network model of V1 trained on natural image inputs using local synaptic plasticity rules [3]. Specifically, if we assume the homeostatically-maintained excitatory firing rate increases with “age” (duration of training), a corresponding decrease in network inhibition follows naturally due to the synaptic plasticity rules that shape network architecture during training. The resulting aged network also exhibits a loss in orientation selectivity (Fig. 1).

In addition to qualitatively replicating previously observed changes, our trained model allows us to probe how the network properties evolve during aging. For example, we statistically characterize how the receptive fields of model neurons change with age: we find that 31% of young model neuron receptive fields are well-characterized as Gabor-like; this drops to 6.5% in the aged network. Only 1.5% of neurons were Gabor-like in both youth and old age, while 5% of neurons that were not classified as Gabor-like in youth were in old age. As one might intuit, these changes are tied to the decrease in orientation selectivity: by remapping the distribution of strengths of the young receptive fields to match the strength distribution of the old receptive fields, while otherwise maintaining the receptive field structure, we can show that orientation selectivity is improved at every age.

Our results demonstrate that deterioration of homeostatic regulation of excitatory firing, coupled with long-term synaptic plasticity, is a sufficient mechanism to reproduce features of observed biogerontological data, specifically declines in selectivity and inhibition. This suggests a potential causality between dysregulation of neuron firing and age-induced changes in brain physiology and performance. While this does not rule out deeper underlying causes or other mechanisms that could give rise to these changes, our approach opens new avenues for exploring these underlying mechanisms in greater depth and making predictions for future experiments.

References

1.
Hua, Li, He, et al. Functional degradation of visual cortical cells in old cats. Neurobiol. Aging 2006, 27, 155–162.
2.
Hua, Kao, Sun, et al. Decreased proportion of GABA neurons accompanies age-related degradation of neuronal function in cat striate cortex. Brain Research Bulletin 2008, 75, 119–125.
3.
King, Zylberberg, DeWeese. Inhibitory Interneurons Decorrelate Excitatory Cells to Drive Sparse Code Formation in a Spiking Model of V1. Journal of Neuroscience 2013, 33, 5475–5485.

P25 Toward a non-perturbative renormalization group analysis of the statistical dynamics of spiking neural populations

Braden Brinkman

Stony Brook University, Department of Neurobiology and Behavior, Stony Brook, NY, United States of America

Correspondence: Braden Brinkman (braden.brinkman@stonybrook.edu)

BMC Neuroscience 2019, 20(Suppl 1):P25

Understanding how the brain processes sensory input and performs computations necessarily demands we understand the collective behavior of networks of neurons. The tools of statistical physics are well-suited to this task, but neural populations present several challenges: neurons are organized in a complicated web of connections–rather than crystalline arrangements statistical physics tools were developed for, neural dynamics are often far from equilibrium, and neurons communicate not by gradual changes in their membrane potential but by all-or-nothing spikes. These all-or-nothing spike dynamics render it difficult to treat neuronal network models using field theoretic techniques, though recently Ocker et al. [1] formulated such a representation for a stochastic spiking model and derived diagrammatic rules to calculate perturbative corrections to the mean field approximation. In this work we use an alternate representation of this model that is amenable to the methods of the non-perturbative renormalization group (NPRG), which has successfully elucidated the different phases of collective behavior in several non-equilibrium models in statistical physics. In particular, we use the NPRG to calculate how stochastic fluctuations modify the nonlinear transfer function of the network, which determines the mean neural firing rates as a function of input, and how these changes depend on network structure. Specifically, the mean field approximation of the neural firing rates r receiving current input I and synaptic connections J is r = f(I+J ∗ r), where f(x) is the nonlinear firing rate of a neuron conditioned on its input x. We show exactly that the true mean, accounting for statistical fluctuations, follows the same form of equation, r = U(I+J ∗ r), where U(x) is an effective nonlinearity to be calculated using NPRG approximation methods.

Reference

1.
Ocker G, Josić K, Shea-Brown E, Buice M. Linking Structure and Activity in Nonlinear Spiking Networks. PLoS Comput Biology 2017, 13(6): e1005583.

P26 Sensorimotor strategies and neuronal representations of whisker-based object recognition in mice barrel cortex

Ramon Nogueira¹, Chris Rodgers¹, Stefano Fusi², Randy Bruno¹

¹Columbia University, Center for Theoretical Neuroscience, New York, NY, United States of America; ²Columbia University, Zuckerman Mind Brain Behavior Institute, New York, United States of America

Correspondence: Ramon Nogueira (rnogueiramanas@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P26

Humans and other animals can identify objects by active touch—coordinated exploratory motion and tactile sensation. Rodents, and in particular mice, scan objects by active whisking, which allows them to form an internal representation of the physical properties of the object. In order to elucidate the behavioral and neural mechanisms underlying this ability, we developed a novel curvature discrimination task for head-fixed mice that challenges the mice to discriminate concave from convex shapes (Fig. 1a). On each trial, a curved shape was presented into the range of the mouse’s whiskers and they were asked to lick left for concave and right for convex shapes. Whisking and contacts were monitored with high-speed video. Mice learned the task well and their performance plateaued at 75.7% correct on average (chance 50% correct).

Because most previous work has relied on mice detecting the presence or location of a simple object with a single whisker, it is a priori unclear what sensorimotor features are important for more complex tasks such as curvature discrimination. To characterize them, we trained a classifier to identify either the stimulus identity or the mouse’s choice on each trial using the entire suite of sensorimotor variables (whisker position, contact timing and position, contact kinematics, etc.) that could potentially drive behavior, as well as task related variables that could also affect behavior (Fig. 1b). By increasing the complexity and richness of the set of features used to perform the classification of stimulus and choice, we identified what features were most informative to perform the task and what features were driving animal’s decision, respectively. We found that the cumulative number of contacts per trial for each whisker independently was informative about the stimulus and choice identity. Surprisingly, precise contact timings within a trial for the different whiskers was not an important feature in either case. Additionally, the exact angular position of each whisker during contacts was highly predictive of the stimulus identity, suggesting that the mice’s behavior was not fully optimal, since this same feature could not predict mice’s choice accurately on a trial-by-trial basis.

In order to identify how barrel cortex contributes to transforming fine-scale representations of sensory events into high-level representations of object identity, we recorded neural populations in mice performing this task. We fit a generalized linear model (GLM) to each neuron’s firing rate as a function of both sensorimotor (e.g., whisker motion and touch) and cognitive (e.g., reward history) variables (Fig. 1c). Neurons responded strongly to whisker touch and, perhaps more surprisingly for a sensory area, to whisker motion. We also observed widespread and unexpected encoding of reward history and choice.

In conclusion, these results show that mice recognize objects by integrating sensory information gathered by active sampling across whiskers. Moreover, we find that the barrel cortex encodes a myriad of sensory and task related variables, like contacts, motor exploration, and reward and choice history, challenging the classical view of barrel cortex as a purely sensory area.

P27 Identifying the neural circuits underlying optomotor control in larval zebrafish

Winnie Lai¹, John Holman¹, Paul Pichler¹, Daniel Saska², Leon Lagnado², Christopher Buckley³

¹University of Sussex, Department of Informatics, Brighton, United Kingdom; ²University of Sussex, Department of Neuroscience, Brighton, United Kingdom; ³University of Sussex, Falmer, United Kingdom

Correspondence: Winnie Lai (wl291@sussex.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P27

Most locomotor behaviours require the brain to instantaneously coordinate a continuous flow of sensory and motor information. As opposed to the conventional open-loop approach in the realm of neuroscience, it has been proposed that the brain is better idealised as a closed-loop controller which regulates dynamical motor actions. Studying brain function on these assumptions remains largely unexplored until the recent emergence of imaging techniques, such as the SPIM, which allow brain-wide neural recording at cellular resolution and high speed during active behaviours. Concurrently, larval zebrafish is becoming a powerful model organism in neuroscience due to their great optical accessibility and robust sensorimotor behaviours. Here, we apply control theory in engineering to investigate the neurobiological basis of the optomotor response (OMR), a body reflex to stabilise optic flow in the presence of whole-field visual motion, in larval zebrafish.

Our group recently developed a collection of OMR models based on variations of proportional-integral controllers. Whilst the proportional term allows rapid response to disturbance, the integral term eliminates the steady-state error over time. We will begin by characterising OMR adaption with respect to different speeds and heights, in both free-swimming and head-restrained environments. Data collected will be used to determine which model best captures zebrafish behaviour. Next, we will conduct functional imaging of fictively behaving animals under a SPIM that our group constructed, in an effort to examine how the control mechanism underpinning OMR is implemented and distributed in the neural circuitry of larval zebrafish. This research project will involve evaluating and validating biological plausible models inspired by control theory, as well as quantifying and analysing large behavioural and calcium imaging data sets. Understanding the dynamical nature of brain function for successful OMR control in larval zebrafish can provide unique insight into the neuropathology of diseases with impaired movement and/or offer potential design solutions for sophisticated prosthetics.

P28 A novel learning mechanism for interval timing based on time cells of hippocampus

Sorinel Oprisan¹, Tristan Aft¹, Mona Buhusi², Catalin Buhusi²

¹College of Charleston, Department of Physics and Astronomy, Charleston, SC, United States of America; ²Utah State University, Department of Psychology, Logan, UT, United States of America

Correspondence: Sorinel Oprisan (oprisans@cofc.edu)

BMC Neuroscience 2019, 20(Suppl 1):P28

Time cells were recently discovered in the hippocampus and they seem to ramp-up their firing when the subject is at a specific temporal marker in a behavioral test. At cellular level, the spread of the firing interval, i.e. the width of the Gaussian-like activity, for each time cell is proportional to the time of the peak activity. Such a linear relationship is well-known at behavioral level and is called scalar property of interval timing.

We proposed a novel mathematical model for interval timing starting with a population of hippocampal time cells and a dynamic learning rule. We hypothesized that during the reinforcement trials the subject learns the boundaries of the temporal duration. Subsequently, a population of time cells is recruited and coverers the entire to-be-timed duration. At this stage, the population of time cells simply produces a uniform average time field since all time cells contribute equally to the average. We hypothesized that dopamine could modulate the activity of time cells during reinforcement trials by enhancing/depressed their activity. Our numerical simulations of the model agree with behavioral experiments.

Acknowledgments: We acknowledge the support of R&D grant from the College of Charleston and support for a Palmetto Academy site from the South Carolina Space Grant Consortium.

References

1.
Oprisan SA, Aft T, Buhusi M, Buhusi CV. Scalar timing in memory: A temporal map in the hippocampus. Journal of Theoretical Biology 2018, 438:133–142.
2.
Oprisan SA, Buhusi M, Buhusi CV. A Population-Based Model of the Temporal Memory in the Hippocampus. Frontiers in Neuroscience 2018, 12:521.

P29 Learning the receptive field properties of complex cells in V1

Yanbo Lian¹, Hamish Meffin², David Grayden¹, Tatiana Kameneva³, Anthony Burkitt¹

¹University of Melbourne, Department of Biomedical Engineering, Melbourne, Australia; ²University of Melbourne, Department of Optometry and Visual Science, Melbourne, Australia; ³Swinburne University of Technology, Telecommunication Electrical Robotics and Biomedical Engineering, Hawthorn, Australia

Correspondence: Anthony Burkitt (aburkitt@unimelb.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P29

There are two distinct classes of cells in the visual cortex: simple cells and complex cells. One defining feature of complex cells is their phase invariance, namely that they respond strongly to oriented bar stimuli with a preferred orientation but with a wide range of phases. A classical model of complex cells is the energy model, in which the responses are the sum of the squared outputs of two linear phase-shifted filters. Although the energy model can capture the observed phase invariance of complex cells, a recent study has shown that complex cells have a great diversity and only a subset can be characterized by the energy model [1]. From the perspective of a hierarchical structure, it is still unclear how a complex cell pools input from simple cells, which simple cells should be pooled, and how strong the pooling weights should be. Most existing models overlook many biologically important details, e.g., some models assume a quadratic nonlinearity of the linear filtered simple cell activity, use pre-determined weights between simple and complex cells, or use artificial learning rules. Hosoya&Hyvarinen [2] applied strong dimension reduction in pooling simple cell receptive fields trained using independent component analysis. Their approach involves pooling simple cells, but the weights connecting simple and complex cells are not learned and thus it is unclear how this can be biophysically implemented.

We propose a biologically plausible learning model for complex cells that pools inputs from simple cells. The model is a 3-layer network with rate-based neurons that describes the activities of LGN cells (layer 1), V1 simple cells (layer 2), and V1 complex cells (layer 3). The first two layers implement a recently proposed simple cell model that is biologically plausible and accounts for many experimental phenomena [3]. The dynamics of the complex cells involves the linear summation of responses of simple cells that are connected to complex cells, taken in our model to be excitatory. Connections between LGN and simple cells are learned based on Hebbian and anti-Hebbian plasticity, similar to that in our previous work [3]. For connections between simple and complex cells that are learned using natural images as input, a modified version of the Bienenstock, Cooper, and Munro (BCM) rule [4] is investigated.

Our results indicate that the learning rule can describe a diversity of individual complex cells, similar to that observed experimentally, that pool inputs from simple cells with similar orientation but differing phases. Preliminary results support the hypothesis that normalized BCM [5] can lead to competition between complex cells and they thereby pool inputs from different groups of simple cells. In summary, this study provides a plausible explanation for how complex cells can be learned using biologically plasticity mechanisms.

References

1.
Almasi A. An investigation of spatial receptive fields of complex cells in the primary visual cortex Doctoral dissertation 2017.
2.
Hosoya H, Hyvärinen A. Learning visual spatial pooling by strong pca dimension reduction. Neural computation 2016 Jul;28(7):1249–64.
3.
Lian Y, Meffin H, Grayden DB, Kameneva T, Burkitt AN. Towards a biologically plausible model of LGN-V1 pathways based on efficient coding. Frontiers in Neural Circuits 2019;13:13.
4.
Bienenstock EL, Cooper LN, Munro PW. Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. Journal of Neuroscience 1982 Jan 1;2(1):32–48.
5.
Willmore BD, Bulstrode H, Tolhurst DJ. Contrast normalization contributes to a biologically-plausible model of receptive-field development in primary visual cortex (V1). Vision research 2012 Feb 1;54:49–60.

P30 Bursting mechanisms based on interplay of the Na/K pump and persistent sodium current

Gennady Cymbalyuk¹, Christian Erxleben², Angela Wenning-Erxleben², Ronald Calabrese²

¹Georgia State University, Neuroscience Institute, Atlanta, GA, United States of America; ²Emory University, Department of Biology, Atlanta, GA, United States of America

Correspondence: Gennady Cymbalyuk (gcymbalyuk@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P30

Central Pattern Generators produce robust bursting activity to control vital rhythmic functions like breathing and leech heart beating under variable environmental and physiological conditions. Their functional operation under different physiological parameters yields distinct dynamic mechanisms based on the dominance of interactions within different subsets of inward and outward currents. Recent studies provide evidence that the Na+/K+ pump contributes to the dynamics of neurons and is a target of neuromodulation [1, 2]. Recently, we have described a complex interaction of the pump current and h-current that plays a role in the dynamics of rhythmic neurons in the leech heartbeat CPG, where the basic building blocks are half-center oscillators (HCOs): pairs of mutually inhibitory HN interneurons producing alternating bursting activity. In the presence of h-current, application of the H+/Na+ antiporter monensin, which stimulates the pump by diffusively increasing the intracellular Na+ concentration [3], dramatically decreases the period of a leech heartbeat HCO by decreasing both the burst duration (BD) and interburst interval (IBI). If h-current is blocked then monensin decreases BD but lengthens IBI so that there is no net change of period with respect to control. This mechanism shows how each phase of bursting, BD and IBI, can be independently controlled by interaction of the pump and h-currents.

We implemented our model [3] into a hybrid system. We investigated a potential role played by the persistent Na+ current (IP), sodium current which does not inactivate. Our hybrid-system allowed us to upregulate or downregulate the Na+/K+ pump and key ionic currents in real-time models and living neurons. We were able to tune the real time model to support functional-like bursting. We investigated how the variation of the basic physiological parameters like conductance and voltage of half-activation of IP and strength of the Na+/K+ pump affect bursting characteristics in single neurons and HCO. We show that interaction of IP and Ipump constitutes a mechanism which is sufficient to support endogenous bursting activity. We show that this mechanism can reinstate robust bursting regime in HN interneurons recorded intracellularly in ganglion 7. Due to interaction of IPand Ipump, the increase of the maximal conductance of IP can shorten the burst duration and expand the interburst interval. Our data also suggest that the functional alternating bursting regime of the HCO network requires the neurons to be in the parametric vicinity of or in the state of the endogenous bursting. We investigated underlying interaction of the IP and Ipump in a simple 2D model describing dynamics of the membrane potential and intracellular Na+ concentration through instantaneous IP and IPump.

Acknowledgements: Supported by NINDS 1 R01 NS085006 to RLC and1 R21 NS111355 to RLC and GSC

References

1.
Tobin AE, Calabrese R. Myomodulin increases Ih and inhibits the NA/K pump to modulate bursting in leech heart interneurons. Journal of neurophysiology 2005 Dec;94(6):3938–50.
2.
Picton LD, Nascimento F, Broadhead MJ, Sillar KT, Miles GB. Sodium pumps mediate activity-dependent changes in mammalian motor networks. Journal of Neuroscience 2017 Jan 25;37(4):906–21.
3.
Kueh D, Barnett W, Cymbalyuk G, Calabrese R. Na(+)/K(+) pump interacts with the h-current to control bursting activity in central pattern generator neurons of leeches. Elife, 2016. Sep 2;5:e19322.

P31 Balanced synaptic strength regulates thalamocortical transmission of informative frequency bands

Alberto Mazzoni¹, Matteo Saponati², Jordi Garcia-Ojalvo³, Enrico Cataldo²

¹Scuola Superiore Sant’Anna Pisa, The Biorobotics Institute, Pisa, Italy; ²University of Pisa, Department of Physics, Pisa, Italy; ³Universitat Pompeu Fabra, Department of Experimental and Health Sciences, Barcelona, Spain

Correspondence: Alberto Mazzoni (a.mazzoni@santannapisa.it)

BMC Neuroscience 2019, 20(Suppl 1):P31

The thalamus receives information about the external world from the peripheral nervous system and conveys it to the cortex. This is not a passive process: the thalamus gates and selects sensory streams through an interplay with its internal activity, and the inputs from the thalamus, in turn, interact in a non-linear way with the functional architecture of the primary sensory cortex. Here we address the network mechanisms by which the thalamus selectively transmits informative frequency bands to the cortex. In particular, spindle oscillations (about 10 Hz) dominate thalamic activity during sleep but are present in the thalamus also during wake [1, 2], and in the awake state are actively filtered out by thalamocortical transmission [3].

To reproduce and understand the filtering mechanism underlying the lack of thalamocortical transmission of spindle oscillations we developed an integrated adaptive exponential integrate-and-fire model of the thalamocortical network. The network is composed by 500 neurons for the thalamus and 5000 neurons for the cortex, with a 1:1 and 1:4 inhibitory to excitatory ratio respectively. We generated the local field potential (LFP) associated to the two networks to compare our simulation with experimental results [3].

Weobserve, in agreement withexperimental data, both delta and theta oscillations in the cortex, but while the cortical delta band is phase locked to thethalamic delta band [4]– even when we take into account the presence of strong colored cortical noise -, the cortical theta fluctuations are not entrained by thalamocortical spindles. Our simulations show that the spindleLFPoscillationsobserved in experimental recordings are way more pronounced in reticular cells than in thalamocortical relays, thus reducing their potential impact on the cortex. More interestingly, we found that the resonance dynamics in the corticalgamma band, generated by the fast interplay between excitation and inhibition, selectively dampens frequencies in the range of spindle oscillations. Finally, by parametrically varying the properties of thalamocortical connections, we found that the transmission of informative frequency bands depends on the balance of the strength of thalamocortical connections toward excitatory and inhibitory neurons in the cortex, coherently with experimental results [5]. Our results pave the way toward an integrated view of the processing of sensory streams from the periphery system to the cortex, and toward in silico design of thalamic neural stimulation.

References

1.
Krishnan GP, Chauvette S, Shamiee I et al. Cellular and neurochemical basis of sleep stages in the thalamocortical network, eLife 2016, e18607.
2.
Barardi A, Garcia-Ojalvo J, Mazzoni A. Transition between Functional Regimes in an Integrate-And-Fire Network Model of the Thalamus. PLoS One 2016, e0161934.
3.
Bastos AM, Briggs F, Alitto HJ, et al. Simultaneous Recordings from the Primary Visual Cortex and Lateral Geniculate Nucleus Reveal Rhythmic Interactions and a Cortical Source for Gamma-Band Oscillations. Journal of Neuroscience 2014, 7639–7644.
4.
Lewis LD, Voigts J, Flores FJ, et al. Thalamic reticular nucleus induces fast and local modulation of arousal state. eLife 2015, e08760.
5.
Sedigh-Sarvestani M, Vigeland L, Fernandez-Lamo I, et al. Intracellular, in vivo, dynamics of thalamocortical synapses in visual cortex. Journal of Neuroscience 2017,5250–5262.

P32 Modeling gephyrin dependent synaptic transmission pathways to understand how gephyrin regulates GABAergic synaptic transmission

Carmen Alina Lupascu¹, Michele Migliore¹, Annunziato Morabito², Federica Ruggeri², Chiara Parisi², Domenico Pimpinella², Rocco Pizzarelli², Giovanni Meli², Silvia Marinelli², Enrico Cherubini², Antonino Cattaneo²

¹Institute of Biophysics, National Research Council, Italy; ²European Brain Research Institute (EBRI), Rome, Italy

Correspondence: Carmen Alina Lupascu (carmen.lupascu@pa.ibf.cnr.it)

BMC Neuroscience 2019, 20(Suppl 1):P32

At inhibitory synapses, GABAergic signaling controls dendritic integration, neural excitability, circuit reorganization and fine tuning of network activity. Among different players, the tubulin-binding protein gephyrin plays a key role in anchoring GABAA receptors to synaptic membranes.

For its properties gephyrin is instrumental in establishing and maintaining a proper excitatory (E)/inhibitory (I) balance necessary for the correct functioning of neuronal networks. A disruption of the E/I balance is thought to be at the origin of several neuropsychiatric disorders including epilepsy, schizophrenia, autism.

In previous studies, the functional role of gephyrin on GABAergic signaling has been studied at post-translational level, using recombinant gephyrin-specific single chain antibody fragments (scFv-gephyrin) containing a nuclear localization signal able to remove endogenous gephyrin from GABAA receptor clusters retargeting it to the nucleus [2]. The reduced accumulation of gephyrin at synapses led to a significant reduction in amplitude and frequency of spontaneous and miniature inhibitory postsynaptic currents (sIPSCs and mIPSCs). This reduction is associated with a decrease in VGAT (the vesicular GABA transporter) and in neuroligin 2 (NLG2), a protein that ensures the cross-talk between the post- and presynaptic sites. Over-expressing NLG2 in gephyrin deprived neurons rescued GABAergic but not glutamatergic innervation, suggesting that the observed changes in the latter were not due to a homeostatic compensatory mechanism. These results suggest a key role of gephyrin in regulating trans-synaptic signaling at inhibitory synapses.

Here, the effects of two different intrabodies against gephyrin have been tested on spontaneous and miniature GABAA-mediated events obtained from cultured hippocampal and cortical neurons. Experimental findings have been used to develop a computational model describing the key role of gephyrin in regulating transynaptic signalingat inhibitory synapses. This represents a further application of a general procedure to study subcellular models of transsynaptic signaling at inhibitory synapses [1]. In this poster we will discuss the statistically significant differences found between the model parameters under control or gephyrin block condition. All computational procedures were carried out using an integrated NEURON and Python parallel code on different systems (JURECA machines, Julich, Germany; MARCONI machine, Cineca, Italy and Neuroscience Gateway, San Diego, USA). The model can be downloaded from the model catalog available on the Collaboratory Portal of Human Brain Project (HBP) (https://collab.humanbrainproject.eu/#/collab/1655/nav/75901?state = model.9f89bbcd-e045-4f1c-97e9-3da5847356c2). The jupyter notebooks used to configure and run the jobs on the HPC machines can be accessed from the Brain Simulation Platform of the HBP (https://collab.humanbrainproject.eu/#/collab/1655/nav/66850).

References

1.
Lupascu CA, Morabito A, Merenda E, et al. A General Procedure to Study Subcellular Models of Transsynaptic Signaling at Inhibitory Synapses. Frontiers in Neuroinformatics 2016;10:23.
2.
Marchionni I, Kasap Z, Mozrzymas JW, Sieghart W, Cherubini E, Zacchi P. New insights on the role of gephyrin in regulating both phasic and tonic GABAergic inhibition in rat hippocampal neurons in culture. Neuroscience 2009 164: 552–562

P33 Proprioceptive feedback effects muscle synergy recruitment during an isometric knee extension task

Hugh Osborne¹, Gareth York², Piyanee Sriya², Marc de Kamps³, Samit Chakrabarty²

¹University of Leeds, Institute for Artificial and Biological Computation, School of Computing, United Kingdomv²University of Leeds, School of Biomedical Sciences, Faculty of Biological Sciences, United Kingdom; ³University of Leeds, School of Computing, Leeds, United Kingdom

Correspondence: Hugh Osborne (sc16ho@leeds.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P33

The muscle synergy hypothesis of motor control posits that simple common patterns of muscle behaviour are combined together to produce complex limb movements. How proprioception influences this process is not clear. EMG recordings were taken of the upper leg muscles during an isometric knee extension task (n = 17, male; 9, female; 8). The internal knee angle was held at 0°, 20°, 60° or 90°. Non-negative matrix factorisation (NMF) was performed on the EMG traces and two synergy patterns were identified accounting for over 90% of the variation across participants. The first synergy indicated the expected increase in activity across all muscles which was also visible in the raw EMG. The second synergy showed a significant difference between coefficients of the knee flexors and extensors, highlighting their agonist/antagonist relationship. As the leg was straightened, the flexor-extensor difference in the second synergy became more pronounced indicating a change in passive insufficiency of the hamstring muscles. Changing hip position and reducing the level of passive insufficiency resulted in delayed onset of the second synergy pattern. An additional observation of bias in the Rectus Femoris and Semitendinosus coefficients of the second synergy was made, perhaps indicating the biarticular behaviour of these muscles.

Having demonstrated that static proprioceptive feedback influences muscle synergy recruitment we then reproduced this pattern of activity in a neural population model. We used the MIIND neural simulation platform to build a network of populations of motor neurons and spinal interneurons with a simple Integrate and Fire neuron model. MIIND provides an intuitive system for developing such networks and simulating with an appropriate and well-defined amount of noise. The simulator can handle large, quick changes in activity with plausible postsynaptic potentials. Two mutually inhibiting populations of both excitatory and inhibitory interneurons were connected to five motor neuron populations, each with a balanced descending input. A single excitatory input to the extensor interneuron pool was used to indicate the level of afferent activity due to the static knee angle. By applying the same NMF step to the activity of the motor neuron populations, the same muscle synergies were observed, with increasing levels of afferent activity resulting in changes to agonist/antagonist recruitment. When the trend in afferent activity is taken further such that it is introduced to the flexor interneuron population, extensor synergy coefficients and vectors increase, leaving the flexor coefficients at zero. This shift from afferent feedback in the agonists to antagonists is predicted by the model but has yet to be confirmed with joint angles beyond 90 degrees.

With the introduction of excitatory connections from the flexor interneuron pool to the Rectus Femoris motor neuron population, the biarticular synergy association, which is proportional to the knee angle, was also reproduced in the model. Even with this addition, there is no need to provide a cortical bias to any individual motor neuron population. The synergies arise naturally from the connectivity of the network and afferent input. This suggests muscle synergies could be generated at the level of spinal interneurons wherein proprioceptive feedback is directly integrated into motor control.

P34 Strategies of dragonfly interception

Frances Chance

Sandia National Laboratories, Department of Cognitive and Emerging Computing, Albuquerque, NM, United States of America

Correspondence: Frances Chance (fschanc@sandia.gov)

BMC Neuroscience 2019, 20(Suppl 1):P34

Interception of a target (e.g. a human catching a ball or an animal catching prey) is a common behavior solved by many animals. However, the underlying strategies used by animals are poorly understood. For example, dragonflies are widely recognized as highly successful hunters, with reports of up to 97% success rates [1], yet a full description of their interception strategy, whether it be to head directly at its target (a strategy commonly referred to as pursuit) or instead to maintain a constant bearing-angle relative to the target (sometimes referred to as proportional or parallel navigation) still has yet to be fully developed (see [2]). While parallel navigation is the logical strategy for calculating the shortest time-to-intercept, we find that there are certain conditions (for example if the prey is capable of relatively quick maneuvers) in which parallel navigation is not the optimal strategy for success. Moreover, recent work [2] observed that dragonflies only adopt a parallel-navigation strategy for a short period of time shortly before prey-capture. We propose that alternate strategies, hybrid between pursuit and parallel navigation lead to more successful interception, and describe what constraints (e.g. prey maneuvering) determine which interception strategy is optimal for the dragonfly. Moreover, we compare dragonfly interception strategy to those that might be employed by other animals, for example other predatory insects that may not be capable of flying speeds similar to those of the dragonfly. Finally, we discuss neural circuit mechanisms by which interception strategy, as well as intercept-maneuvers, may be calculated based on prey-image slippage on the dragonfly retina.

This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.

Acknowledgements: Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. SAND2019-2782A

References

1.
Olberg RM, Worthington AH, Venator KR. Prey pursuit and interception in dragonflies. Journal of Comparative Physiology A 2000 Feb 1;186(2):155–62.
2.
Mischiati M, Lin HT, Herole O, Imler E, Olberg R, Leonardo, A. Internal models direct dragonfly interception steering. Nature 2015, 517: 333–338.

P35 The bump attractor model predicts spatial working memory impairment from changes to pyramidal neurons in the aging rhesus monkey dlPFC

Sara Ibanez Solas¹, Jennifer Luebke², Christina Weaver¹, Wayne Chang²

¹Franklin and Marshall College, Department of Mathematics and Computer Science, Lancaster, PA, United States of America; ²Boston University School of Medicine, Department of Anatomy and Neurobiology, Boston, MA, United States of America

Correspondence: Sara Ibanez Solas (sibanezs@fandm.edu)

BMC Neuroscience 2019, 20(Suppl 1):P35

Behavioral studies have shown impairment in performance during spatial working memory (WM) tasks with aging in several animal species, including humans. Persistent activity (PA) during delay periods of spatial WM tasks is thought to be the main mechanism underlying spatial WM, since the selective firing of pyramidal neurons in the dorsolateral prefrontal cortex (dlPFC) to different spatial locations seems to encode the memory of the stimulus. This firing activity is generated by recurrent connections between layer 3 pyramidal neurons in the dlPFC, which, as many in vitro studies have shown, undergo significant structural and functional changes with aging. However, the extent to which these changes affect the neural mechanisms underlying spatial WM, and thus cognition, is not known. Here we present the first empirical evidence that spatial WM in the rhesus monkey is impaired in some middle-aged subjects, and show that spatial WM performance is negatively correlated with hyperexcitability (increased action potential firing rates) of layer 3 pyramidal neurons. We used the bump attractor network model to explore the effects on spatial WM of two age-related changes to the properties of individual pyramidal neurons: the increased excitability observed here and previously [1, 2], and a 10-30% loss of both excitatory and inhibitory synapses in middle-aged and aged monkeys [3]. In particular, we simulated the widely used (Oculomotor) Delayed Response Task (DRT) and introduced a simplified model of the Delayed Recognition Span Task-spatial condition (DRST-s) which was administered to the monkeys in this study. The DRST-s task is much more complex than the DRT, requiring simultaneous encoding of multiple stimuli which successively increase in number. Simulations predicted that PA—and in turn WM performance—in both tasks was severely impaired by the increased excitability of individual neurons, but not by the loss of synapses alone. This is consistent with the finding in [3], where no correlations were seen between synapse loss and DRST-s impairment. Simulations also showed that pyramidal neuron hyperexcitability and synapse loss might compensate each other partially: the level of impairment in the DRST-s model with these simultaneous changes was similar to that seen in the DRST-s data from young vs. aged monkeys. The models also predict an age-related reduction in total synaptic input current to pyramidal neurons alongside changes to their f-I curves, showing that the increased excitability of pyramidal neurons we have seen in vitro is consistent with lower firing rates seen during DRT testing of middle-aged and aged monkeys in vivo [4]. Finally, in addition to PA, this study suggests that short-term synaptic facilitation plays an important (if often unappreciated) role in spatial WM.

Acknowledgments: We thank National Institute of Health (National Institute on Aging) for supporting the authors with Grant Number R01AG059028.

References

1.
Chang YM, Rosene DL, Killiany RJ, Mangiamele LA, Luebke JI. Increased action potential firing rates of layer 2/3 pyramidal cells in the prefrontal cortex are significantly related to cognitive performance in aged monkeys. Cerebral Cortex 2004 Aug 5;15(4):409–18.
2.
Coskren PJ, Luebke JI, Kabaso D, et al. Functional consequences of age-related morphologic changes to pyramidal neurons of the rhesus monkey prefrontal cortex. Journal of computational neuroscience 2015 Apr 1;38(2):263–83.
3.
Peters A, Sethares C, Luebke JI. Synapses are lost during aging in the primate prefrontal cortex. Neuroscience 2008 Apr 9;152(4):970–81.
4.
Wang M, Gamo NJ, Yang Y, et al. Neuronal basis of age-related working memory decline. Nature 2011 Aug;476(7359):210.

P36 Brain dynamic functional connectivity: lesson from temporal derivatives and autocorrelations

Jeremi Ochab¹, Wojciech Tarnowski¹, Maciej Nowak^1,2, Dante Chialvo³

¹Jagiellonian University, Institute of Physics, Kraków, Poland; ²Mark Kac Complex Systems Research Center, Kraków, Poland; ³Universidad Nacional de San Martín and CONICET, Center for Complex Systems & Brain Sciences (CEMSC^3), Buenos Aires, Argentina

Correspondence: Jeremi Ochab (jeremi.ochab@uj.edu.pl)

BMC Neuroscience 2019, 20(Suppl 1):P36

The study of correlations between brain regions in functional magnetic resonance imaging (fMRI) is an important chapter of the analysis of large-scale brain spatiotemporal dynamics. The burst of research exploring momentary patterns of blood oxygen level-dependent (BOLD) coactivations, referred to as dynamic functional connectivity, has brought prospects of novel insights into brain function and dysfunction. It has been, however, closely followed by inquiries into pitfalls the new methods hold [1], and only recently by their systematic evaluation [2].

From among such recent measures, we scrutinize a metric dubbed “Multiplication of Temporal Derivatives” (MTD) [3] which is based on the temporal derivative of each time series. We compare it with the sliding window Pearson correlation of the raw time series in several stationary and non-stationary set-ups, including: simulated autoregressive models with a step change in their coupling, surrogate data [4] with realistic spectral and covariance properties and a step change in their cross- and autocovariance (see, Fig. 1, right panels), and a realistic stationary network detection (with the use of gold standard simulated data; [5]).

The formal comparison of the MTD formula with the Pearson correlation of the derivatives reveals only minor differences, which we find negligible in practice. The numerical comparison reveals lower sensitivity of derivatives to low frequency drifts and to autocorrelations but also lower signal-to-noise ratio. It does not indicate any evident mathematical advantages of the MTD metric over commonly used correlation methods.

Along the way we discover that cross-correlations between fMRI time series of brain regions are tied to their autocorrelations (see, Fig. 1, left panel). We solve simple autoregressive models to provide mathematical grounds for that behaviour. This observation is relevant to the occurrence of false positives in real networks and might be an unexpected consequence of current preprocessing techniques. This fact remains troubling, since similar autocorrelations of any two brain regions do not necessarily result from their actual structural connectivity or functional correlation.

The study has been recently published [6].

Acknowledgements: Work supported by the National Science Centre (Poland) grant DEC-2015/17/D/ST2/03492 (JKO), Polish Ministry of Science and Higher Education ”Diamond Grant” 0225/DIA/2015/44 (WT), and by CONICET (Argentina) and Escuela de Ciencia y Tecnología, UNSAM (DRC).

References

1.
Hindriks R, Adhikari MH, Murayama Y et al. Can sliding-window correlations reveal dynamic functional connectivity in resting-state fMRI? Neuroimage 2016, 127, 242–256.
2.
Thompson WH, Richter CG, Plavén-Sigray P, Fransson P. Simulations to benchmark time-varying connectivity methods for fMRI. PLoS Computational Biology 2018, 14, e1006196.
3.
Shine JM, Koyejo O, Bell PT, et al. Estimation of dynamic functional connectivity using multiplication of temporal derivatives. Neuroimage 2015, 122, 399–407.
4.
Laumann TO, Snyder AZ, Mitra A. et al. On the stability of BOLD fMRI correlations. Cereb Cortex 2017, 27, 4719–4732.
5.
Smith SM, Miller KL, Salimi-Khorshidi G. et al. Network modelling methods for FMRI. Neuroimage 2011, 54, 875–891.
6.
Ochab JK, Tarnowski W, Nowak MA, Chialvo DR. On the pros and cons of using temporal derivatives to assess brain functional connectivity. Neuroimage 2019, 184, 577–585.

P37 nigeLab: a fully featured open source neurophysiological data analysis toolbox

Federico Barban¹, Maxwell D. Murphy², Stefano Buccelli¹, Michela Chiappalone¹

¹Fondazione Istituto Italiano di Tecnologia, Rehab Technologies, IIT-INAIL Lab, Genova, Italy; ²University of Kansas Medical Center, Department of Physical Medicine and Rehabilitation, Kansas City, United States of America

Correspondence: Federico Barban (federico.barban@iit.it)

BMC Neuroscience 2019, 20(Suppl 1):P37

The rapid advance in neuroscience research and the related technological improvements have led to an exponential increase in the ability to collect high-density neurophysiological signals from extracellular field potentials generated by neurons. While the specific processing of these signals is dependent upon the nature of the system under consideration, many studies seek to relate these signals to behavioral or sensory stimuli and typically follow a similar workflow. In this context we felt the need for a tool that facilitates tracking and organizing data across experiments and experimental groups during the processing steps. Moreover, we sought to unify different resources into a single hub that could offer standardization and interoperability between different platforms, boosting productivity and fostering the open exchange of experimental data between collaborating groups.

To achieve this, we built an end-to-end signal analysis package based on MATLAB, with a strong focus on collaboration, organization and data sharing . Inspired by the FAIR data policy [1], we propose a hierarchical data organization with copious amount of metadata, to help keep everything organized, easily shareable and traceable. The result is the neuroscience integrated general electrophysiology lab, or nigeLab, a unified package for tracking and analyzing electrophysiological and behavioral endpoints in neuroscientific experiments. The pipeline has a lot to offer: data extraction to a standard hierarchical format, filtering algorithms with local field potential (LFP) extraction, spike detection and spike sorting, point process analysis, frequency content analysis, graph theory and connectivity analysis both in the spike domain and in the LFP as well as many data visualizations tools and interfaces.

The source code is freely available and developed to be easily expandable and adaptable to different setups and paradigms. Importantly, nigeLab focuses on ease-of-use through an intuitive interface. We aimed to design an easily deployable toolkit for scientists with a non-technical background, while still offering powerful tools for electrophysiological pre-processing, analysis, and metadata tracking. The whole pipeline is lightweight and optimized to be scalable and parallelizable and can be run on a laptop as well as on a cluster.

Reference

1.
European Commission. Guidelines on FAIR Data Management in Horizon 2020.

P38 Neural ensemble circuits with adaptive resonance frequency

Alejandro Tabas¹, Shih-Cheng Chien²

¹Max Planck Institute for Human Cognitive and Brain Sciences, Research Group in Neural Mechanisms of Human Communication, Leipzig, Germany; ²Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany

Correspondence: Alejandro Tabas (alextabas@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P38

Frequency modulation is a ubiquitous phenomenon in sensory processing and cortical communication. Although multiple neural mechanisms are known to operate at cortical and subcortical levels of the auditory hierarchy to encode fast FM-modulation, the neural encoding of low-rate FM-modulation are still poorly understood. In this work, we introduce a potential neural mechanism for low-rate FM selectivity based on a simplified model of a cortical microcolumn following Wilson-Cowan dynamics.

Previous studies have used Wilson-Cowan microcircuits with one excitatory and one inhibitory population to build a system responding selectively to certain rhythms [1]. The excitatory ensemble is connected to the circuit’s input, that usually consists of a sinusoid or a similarly periodic input. The system incorporates synaptic depression through adaptation variables that reduce the effective connectivity weights between the neural populations [2]. By carefully tuning the system parameters, May and Tiitinen showed that this system shows resonant behaviour to a narrow range of frequencies of the oscillatory input, effectively acting as a periodicity detector [1].

Here, we first provide for an approximate analytical expression of the resonance frequency of the system with the system parameters. First, we subdivide the Wilson-Cowan dynamics in two dynamical systems operating at two different temporal scales: the fast system, that operates at the timescale of the cell membrane time constants (tau ~ 10-20ms [3]), and the slow system, that operates at the timescale of the adaptation time constant (tau = 500ms [2]). In the timescale of the fast system, the adaptation dynamics are quasistatic and the connectivity weights can be regarded as locally constant. Under these conditions, we show that the Wilson-Cowan microcircuit behaves as a driven damped harmonic oscillator whose damping factor and resonant frequency depend on the connectivity weights between the populations. We validate the analytical predictions with numerical simulations of the non-approximated system with different sinusoidal inputs and show that our analytical predictions explain the previous results from May and Tiitinen [1].

In the timescale of the slow system, fast oscillations in the firing rate of the excitatory and inhibitory populations are smoothed down by the effective low-pass filtering exerted by the much slower adaptation dynamics. Under these conditions, the connectivity weights decay slowly at a constant rate that depends on the average firing rates of the neural populations and the adaptation strengths. However, since the nominal resonance frequency depends on the connectivity weights, the decay of the latter results in a modulation of the former. We exploit this property to build a series of architectures that potentially show direction selectivity to rising or falling frequency modulated sinusoids. Our analytical predictions are validated by numerical simulations of the non-approximated system, driven by frequency modulated sinusoidal inputs.

References

1.
May P, Tiitinen H. Human cortical processing of auditory events over time. NeuroReport 2001 Mar 5;12(3):573–7.
2.
May P, Tiitinen H. Temporal binding of sound emerges out of anatomical structure and synaptic dynamics of auditory cortex. Frontiers in computational neuroscience 2013 Nov 7;7:152.
3.
McCormick DA, Connors BW, Lighthall JW, Prince DA. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. Journal of neurophysiology 1985 Oct 1;54(4):782–806.

P39 Large-scale cortical modes reorganize between infant sleep states and predict preterm development

James Roberts¹, Anton Tokariev², Andrew Zalesky³, Xuelong Zhao⁴, Sampsa Vanhatalo², Michael Breakspear⁵, Luca Cocchi⁶

¹QIMR Berghofer Medical Research Institute, Brain Modelling Group, Brisbane, Australia; ²University of Helsinki, Department of Clinical Neurophysiology, Helsinki, Finland; ³University of Melbourne, Melbourne Neuropsychiatry Centre, Melbourne, Australia; ⁴University of Pennsylvania, Department of Neuroscience, Philadelphia, United States of America; ⁵QIMR Berghofer Medical Research Institute, Systems Neuroscience Group, Brisbane, Australia; ⁶QIMR Berghofer Medical Research Institute, Clinical Brain Networks Group, Brisbane, Australia

Correspondence: James Roberts (james.roberts@qimrberghofer.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P39

Sleep architecture carries important information about brain health but mechanisms at the cortical scale remain incompletely understood. This is particularly so in infants, where there are two main sleep states: active sleep and quiet sleep, precursors to the adult REM and NREM. Here we show that active compared to quiet sleep in infants heralds a marked change from long- to short-range functional connectivity across broad-frequency neural activity. This change in cortical connectivity is attenuated following preterm birth and predicts visual performance at two years. Using eigenmodes of brain activity [1] derived from neural field theory [2], we show that active sleep primarily exhibits reduced energy in a large-scale, uniform mode of neural activity and slightly increased energy in two non-uniform anteroposterior modes. This energy redistribution leads to the emergence of more complex connectivity patterns in active sleep compared to quiet sleep. Preterm-born infants show an attenuation in this sleep-related reorganization of connectivity that carries novel prognostic information. We thus provide a mechanism for the observed changes in functional connectivity between sleep states, with potential clinical relevance.

Acknowledgments: A.T. was supported by Finnish Cultural Foundation (Suomen Kulttuurirahasto; 00161034). A.T. and S.V. were also funded by Academy of Finland (276523 and 288220) and Sigrid Jusélius Foundation (Sigrid Juséliuksen Säätiö), as well as Finnish Pediatric Foundation (Lastentautien tutkimussäätiö). J.R., A.Z., M.B., and L.C. are supported by the Australian National Health Medical Research Council (J.R. 1144936 and 1145168, A.Z. 1047648, M.B. 1037196, L.C. 1099082 and 1138711). This work was also supported by the Rebecca L. Cooper Foundation (J.R., PG2018109) and the Australian Research Council Centre of Excellence for Integrative Brain Function (M.B., CE140100007).

References

1.
Atasoy S, Donnelly I, Pearson J. Human brain networks function in connectome-specific harmonic waves. Nature communications 2016 Jan 21;7:10340.
2.
Robinson PA, Zhao X, Aquino KM, Griffiths JD, Sarkar S, Mehta-Pandejee G. Eigenmodes of brain activity: Neural field theory predictions and comparison with experiment. NeuroImage 2016 Nov 15;142:79–98.

P40 Reliable information processing through self-organizing synfire chains

Thomas Ilett, David Hogg, Netta Cohen

University of Leeds, School of Computing, Leeds, United Kingdom

Correspondence: Thomas Ilett (tomilett@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P40

Reliable information processing in the brain requires precise transmission of signals across large neuron populations that is reproducible and stable over time. Exactly how this is achieved remains an open question but a large body of experimental data has pointed to the importance of synchronised firing patterns of cell assemblies in mediating precise sequential patterns of activity. Synfire chains provide an appealing theoretical framework to account for reliable transmission of information through a network, with potential for robustness to noise and synaptic degradation. Here, we use self-assembled synfire chain models to test the interplay between encoding capacity, robustness to noise and flexibility to learning new patterns. We first model synfire chain development as a self-assembly process from a randomly connected network of leaky integrate-and-fire (LIF) neurons subject to a variant of the spike-timing-dependent plasticity (STDP) learning rule (adapted from [1]). We show conditions for these networks to form chains (in some conditions even without external input) and characterise the encoding capacity of the network by presenting different input patterns that result in distinguishable chains of activation. We show that these networks develop different, often overlapping chains in response to different inputs. We further demonstrate the importance of inhibition for the long-term stability of the chains and test the robustness of our network to various degrees of neuronal and synaptic death. Finally, we explore the ability for the network to increase its encoding capacity by dynamically learning new inputs.

Reference

1.
Waddington A, Appleby PA, De Kamps M, Cohen N. Triphasic spike-timing-dependent plasticity organizes networks to produce robust sequences of neural activity. Frontiers in Computational Neuroscience 2012 Nov 12;6:88.

P41 Acetylcholine regulates redistribution of synaptic efficacy in neocortical microcircuitry

Cristina Colangelo

Blue Brain Project (BBP), Brain Mind Institute, EPFL, Lausanne, Switzerland, geneva, Switzerland

Correspondence: Cristina Colangelo (cristina.colangelo@epfl.ch)

BMC Neuroscience 2019, 20(Suppl 1):P41

Acetylcholine is one of the most widely characterized neuromodulatory systems involved in the regulation of cortical activity. Cholinergic release from the basal forebrain controls neocortical network activity and shapes behavioral states such as learning and memory. However, a precise understanding of how acetylcholine regulates local cellular physiology and synaptic transmission that reconfigure global brain states remains poorly understood. To fill this knowledge gap, we analyzed whole-cell patch-clamp recordings from connected pairs of neocortical neurons to investigate how acetylcholine release modulates membrane properties and synaptic transmission. We found that bath-application of 10 µM carbachol differentially redistributes the available synaptic efficacy and the short-term dynamics of excitatory and inhibitory connections. We propose that redistribution of synaptic efficacy by acetylcholine is a potential means to alter content, rather than the gain of information transfer of synaptic connections between specific cell-types types in the neocortex. Additionally, we provide a dataset that can serve as reference to build data-driven computational models on the role of ACh in governing brain states.

P42 NeuroGym: A framework for training any model on more than 50 neuroscience paradigms

Manuel Molano-Mazon¹, Guangyu Robert Yang², Christopher Cueva², Jaime de la Rocha¹, Albert Compte³

¹IDIBAPS, Theoretical Neurobiology, Barcelona, Spain; ²Columbia University, Center for Theoretical Neuroscience, New York, United States of America; ³IDIBAPS, Systems Neuroscience, Barcelona, Spain

Correspondence: Manuel Molano-Mazon (molano@clinic.cat)

BMC Neuroscience 2019, 20(Suppl 1):P42

It is becoming increasingly popular in systems neuroscience to train Artificial Neural Networks (ANNs) to investigate the neural mechanisms that allow animals to display complex behavior. Important aspects of brain function such as perception or working memory [2, 4] have been investigated using this approach, which has yielded new hypotheses about the computational strategies used by brain circuits to solve different behavioral tasks.

While ANNs are usually tuned for a small set of closely related tasks, the ultimate goal when training neural networks must be to find a model that can explain a wide range of experimental results collected across many different tasks. A necessary step towards that goal is to develop a large, standardized set of neuroscience tasks on which different models can be trained. Indeed, there is a large body of experimental work that hinges on a number of canonical behavioral tasks that have become a reference in the field (e.g. [2,4]) and that makes it possible to develop a general framework encompassing many relevant tasks on which neural networks can be trained.

Here we propose a comprehensive toolkit, NeuroGym, that allows training any network model on many established neuroscience tasks using Reinforcement Learning techniques. NeuroGym currently contains more than ten classical behavioral tasks including, working memory tasks (e.g. [4]), value-based decision tasks (e.g. [3]) and context-dependent perceptual categorization tasks (e.g. [2]). In providing this toolbox our aim is twofold: (1) to facilitate the evaluation of any network model on many tasks and thus evaluate its capacity to generalize to and explain different experimental datasets; (2) to standardize the way computational neuroscientists implement behavioral tasks, in order to promote benchmarking and replication.

Inheriting all functionalities from the machine learning toolkit Gym (OpenAI), NeuroGym allows a wide range of well-established machine learning algorithms to be easily trained on behavioral paradigms relevant for the neuroscience community. NeuroGym also incorporates several properties and functions (e.g. realistic time step or separation of training into trials) that are specific to the protocols used in neuroscience.

Furthermore, the toolkit includes various modifier functions that greatly expand the space of available tasks. For instance, users can introduce trial-to-trial correlations onto any task [1]. Also, tasks can be combined so as to test the capacity of a given model to perform two tasks simultaneously (e.g. to study interference between two tasks [5]).

In summary, NeuroGym constitutes an easy-to-use toolkit that considerably facilitates the evaluation of a network model that has been tuned for a particular task on more than 50 tasks with no additional work, and proposes a framework to which computational neuroscience practitioners can contribute by adding tasks of their interest, using a straightforward template.

Acknowledgments: The Spanish Ministry of Science, Innovation and Universities, the European Regional Development Fund (grant BFU2015-65315-R), by Generalitat de Catalunya (grants 2017 SGR 1565 and 2017-BP-00305) and the European Research Council (ERC-2015-CoG–683209_PRIORS).

References

1.
Hermoso-Mendizabal A, Hyafil A, Rueda-Orozco PE, Jaramillo S, Robbe D, de la Rocha J. Response outcomes gate the impact of expectations on perceptual decisions. bioRxiv 2019 Jan 1:433409.
2.
Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 2013 Nov;503(7474):78.
3.
Padoa-Schioppa C, Assad JA. Neurons in the orbitofrontal cortex encode economic value. Nature 2006 May;441(7090):223.
4.
Romo R, Brody CD, Hernández A, Lemus L. Neuronal correlates of parametric working memory in the prefrontal cortex. Nature 1999 Jun;399(6735):470.
5.
Zhang X, Yan W, Wang W, et al. Active information maintenance in working memory by a sensory cortex. bioRxiv 2018 Jan 1:385393.

P43 Synaptic dysfunctions underlying reduced working memory serial bias in autoimmune encephalitis and schizophrenia

Heike Stein¹, Joao Barbosa¹, Adrià Galán¹, Alba Morato², Laia Prades², Mireia Rosa³, Eugenia Martínez⁴, Helena Ariño⁴, Josep Dalmau⁴, Albert Compte³

¹Institut d’Investigacions Biomèdiques August Pi i Sunyer (²IDIBAPS), Theoretical Neurobiology, Barcelona, Spain; ²IDIBAPS, Neuroscience, Barcelona, Spain; ³Hospital Clinic, Pediatric Psychiatry, Barcelona, Spain; ⁴IDIBAPS, Neuroimmunology, Barcelona, Spain

Correspondence: Heike Stein (heike.c.stein@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P43

Continuity of mnemonic contents in time contributes to forming coherent memory representations. Recently, attractive response biases towards previously memorized features in delayed-response tasks have been reported as evidence for the continuous integration of working memory (WM) contents between trials [1]. In turn, brain disorders with reported executive and memory dysfunction may be characterized by reduced WM serial bias [2], revealing reduced temporal coherence of memory representations. To gain mechanistic insight into this effect, we tested a unique population of patients recovering from anti-NMDAR encephalitis patients, an immune-mediated brain disease causing a drastic reduction of NMDARs, accompanied by WM deficits even as receptors return to normal levels [3]. We hypothesized that potential changes in serial biases found in anti-NMDAR encephalitis should be qualitatively similar to changes in schizophrenia, a disorder associated with hypofunctional NMDARs. We collected behavioral data from anti-NMDAR encephalitis patients, schizophrenic patients, and healthy controls performing a visuospatial WM task. While healthy controls’ responses were significantly biased towards previously remembered locations in the presence of WM requirements (delays of several seconds), attractive serial biases were reduced in encephalitis, and absent in schizophrenic patients. We modeled these findings using a recurrent spiking network with synaptic short-term facilitation in excitatory connections. In this model, memory-sustaining bumps of persistent activity decay after the memory delay but leave stimulus-specific, facilitated synaptic ‘traces’ that affect neural dynamics in the next trial. We systematically explored parameters of synaptic transmission and short-term plasticity to determine the mechanism that could reduce attractive serial bias. By altering the parameters of short-term facilitation, we reproduced reduced and absent attractive biases in patient groups, while maintaining WM precision at a constant level across groups, an intriguing finding from our behavioral analyses. This manipulation of short-term facilitation is in accordance with studies in cortical slices from mouse models of schizophrenia [4]. We thus propose that serial biases in visuospatial WM provide a behavioral readout of short-term facilitation dysfunction in anti-NMDAR encephalitis and schizophrenia.

Acknowledgements: Funding provided by Institute Carlos III, Spain (grant PIE 16/00014), Cellex Foundation, the Spanish Ministry of Science, Innovation and Universities (grant BFU 2015-65318-R), the European Regional Development Fund, the Generalitat de Catalunya (grant AGAUR 2017 SGR 1565), “la Caixa” (LCF/BQ/IN17/11620008, H.S.), and the European Union’s Horizon 2020 Marie Skłodowska-Curie grant (713673, H.S.).

References

1.
Fischer J, Whitney D. Serial dependence in visual perception. Nature Neuroscience 2014, 17, 738–743
2.
Lieder I, Adam V, Frenkel O, et al. Perceptual bias reveals slow-updating in autism and fast-forgetting in dyslexia. Nature Neuroscience 2019, 22, 256–264
3.
Dalmau J, Lancaster E, Martinez-Hernandez E, et al. Clinical experience and laboratory investigations in patients with anti-NMDAR encephalitis. Lancet Neurology 2011, 10, 63–74
4.
Arguello P, Gogos J. Genetic and cognitive windows into circuit mechanisms of psychiatric disease. Trends in Neuroscience 2012, 35, 3–13

P44 Effects of heterogeneity in neuronal electric properties on the intrinsic dynamics of cortical networks

Svetlana Gladycheva¹, David Boothe², Alfred Yu², Kelvin Oie², Athena Claudio¹, Bailey Conrad¹

¹Towson University, Department of Physics, Astronomy and Geosciences, Towson, MD, United States of America; ²U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: Svetlana Gladycheva (sgladycheva@towson.edu)

BMC Neuroscience 2019, 20(Suppl 1):P44

In previous large-scale models of neural systems, neurons of the same class are typically identical. By contrast, real systems exhibit significant cell-to-cell diversity at different levels, from morphology to intrinsic cell properties [1] to synaptic properties [2]. This heterogeneity may affect neural information processing by, for example, helping to integrate diverse inputs to the network [1], or by positively contributing to the stability of the network activity [3]. However, the exact role of neural heterogeneity in large-scale neural systems is not fully understood.

We examine the impact of neural heterogeneity in large-scale neural models. We use an adaptation of the Traub’s single-column thalamocortical network model [4], adapted to the PGENESIS parallel simulation environment [5]. The model is tuned to eliminate intrinsic neuronal activity and is randomly driven with independent Poisson-distributed excitatory postsynaptic noise potentials with an average firing rate between 1-10 Hz.

Network activity is assessed by calculating the mean local field potential (LFP) and analyzing the neuronal spiking activity. We explored changes in network parameters, including local connectivity probability; the parameters of the noise inputs; and the relative strength of synaptic weights. Observed LFPs can generally be classified into two patterns: an aperiodic low-activity state and a high-activity state involving persistent oscillations associated with periodic neuronal firing. At a broad range of the connectivity probabilities, the network stays in low-activity state until a “threshold” level of connectivity is reached. Further increase in connectivity moves model behavior into high-activity regimes and alters the frequency spectrum. Changes in parameters of noise inputs (frequency range, weight, and percentage of neurons receiving noise) elicit similar threshold-like behavior, as do changes in the ratio of excitatory-to-inhibitory synaptic weights, with high-activity states observed in networks with weak inhibition. We introduce heterogeneity in the intrinsic biophysical parameters by randomizing the values of the anomalous rectifier (AR) channels’ conductance in the model’s pyramidal neurons. Preliminary results from effects of heterogeneity on network activity will be shown. In addition, network responses to pulse train stimuli input to the pyramidal cells at different locations in the column will be studied.

References

1.
Adams NE, et al. Heterogeneity in neuronal intrinsic properties: a possible mechanism for hub-like properties of the rat anterior cingulate cortex during network activity. eNeuro 2017, 0313–16
2.
Thomson AM, et al, Single axon IPSPs elicited in pyramidal cells by three classes of interneurons in slices of rat neocortex. Journal of Physiology 1996, 496:81–102
3.
Mejias JF, Longtin A, Differential effects of excitatory and inhibitory heterogeneity on the gain and asynchronous state of sparse cortical networks. Frontiers in Computational Neuroscience 2014, 8:107
4.
Traub RD, et al, Single column thalamocortical network model exhibiting gamma oscillations, sleep spindles and epileptic bursts. Journal of Neurophysiology 2005, 93(4):2194–232
5.
Boothe, et al, Impact of neuronal membrane damage on a local field potential in a large-scale simulation of the neuronal cortex. Frontiers in Neurology 2017, 8:236

P45 Structure–function multi-scale connectomics reveals a major role of the fronto-striato-thalamic circuit in brain aging

Paolo Bonifazi¹, Asier Erramuzpe¹, Ibai Diez¹, Iñigo Gabilondo¹, Matthieu Boisgontier², Lisa Pauwels², Sebastiano Stramaglia³, Stephan Swinnen², Jesus Cortes¹

¹Biocruces Health Research Institute, Computational Neuroimaging, Barakaldo, Spain; ²Katholieke Universiteit Leuven, Department of Movement Sciences, Leuven, Belgium; ³University of Bari, Physics, Bari, Italy

Correspondence: Paolo Bonifazi (paol.bonifazi@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P45

Physiological aging affects brain structure and function impacting morphology, connectivity, and performance. However, whether some brain connectivity metrics might reflect the age of an individual is still unclear. Here, we collected brain images from healthy participants (N = 155) ranging from 10 to 80 years to build functional (resting state) and structural (tractography) connectivity matrices, both data sets combined to obtain different connectivity features. We then calculated the brain connectome age—an age estimator resulting from a multi-scale methodology applied to the structure–function connectome, and compared it to the chronological age (ChA). Our results were twofold. First, we found that aging widely affects the connectivity of multiple structures, such as anterior cingulate and medial prefrontal cortices, basal ganglia, thalamus, insula, cingulum, hippocampus, parahippocampus, occipital cortex, fusiform, precuneus, and temporal pole. Second, we found that the connectivity between basal ganglia and thalamus to frontal areas, also known as the fronto-striato-thalamic (FST) circuit, makes the major contribution to age estimation. In conclusion, our results highlight the key role played by the FST circuit in the process of healthy aging. Notably, the same methodology can be generally applied to identify the structural–functional connectivity patterns correlating to other biomarkers than ChA.

P46 Studying evoked potentials in large cortical networks with PGENESIS 2.4

David Beeman¹, Alfred Yu², Joshua Crone³

¹University of Colorado, Department of Electrical, Computer and Energy Engineering, Boulder, CO, United States of America; ²U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, MD, United States of America; ³U.S. Army Research Laboratory, Computational and Information Sciences Directorate, Aberdeen Proving Ground, MD, MD, United States of America

Correspondence: David Beeman (dbeeman@colorado.edu)

BMC Neuroscience 2019, 20(Suppl 1):P46

Modern neural simulators have been developed for large scale network models of single-compartment integrate-and-fire neurons that efficiently model millions of neurons. However, accurate modeling of neural activity, including evoked potentials (EPs) recorded from scalp or cortical surface electrodes, requires multicompartmental neuron models with enough realism in the dendritic morphology and location of synapses to account for the major sinks and sources of currents in the extracellular medium. The GENESIS simulator (http://genesis-sim.org) and its parallel computer version PGENESIS were developed over 30 years ago for structurally realistic modeling of large cortical networks. Today, GENESIS continues to be updated with new features and used for implementing such models. Recently Kudela, et al. [1] used a large GENESIS network model to study effects of short-term synaptic plasticity on adaptation of EPs in auditory cortex. Our plans are to increase the size and cell density, extend the model to other cortical layers, and to run simulations on supercomputers such as those available through NSG (the Neuroscience Gateway portal, https://www.nsgportal.org) [2]. Crone, et al. [3] have modified the 2006 release of GENESIS and PGENESIS 2.3 to allow simulations of networks of up to 9 million neurons. Their modifications addressed memory management, reproducibility, and other issues that limited model scalability on high performance computing resources. These improvements are now merged with the current GENESIS/PGENESIS 2.4 development versions. This official release of PGENESIS 2.4 and GENESIS 2.4 are available from the Repository for Continued Development of the GENESIS 2.4 Neural Simulator (https://github.com/genesis-sim/genesis-2.4). We used the new PGENESIS to simulate EPs measured 2 mm above a patch of layer 2/3 primary auditory cortex (Fig. 1), as in [1]. The network was divided into 24 slices simulated in parallel. This model uses 17-compartment pyramidal cells (PCs) based on human cortical PC reconstructions. Inhibition is provided from model basket cells (BCs). Short tone pulses produce excitation to PC distal basal dendrites. Subsequently, PC-PC excitation occurs at oblique apical dendrites. It was shown in [1] that these two excitatory currents produce oppositely oriented electric dipolar charges that are responsible for the initial vertex-positive P1 peak and the following vertex-negative N1 peak in the EP. These results show the effect of varying the strength of the inhibition at the PC proximal apical dendrite from BCs. This occurs later in the N1 peak, and produces a dipole that is oriented oppositely to the one that causes the N1 peak. Therefore, increased inhibition narrows the peak. With PGENESIS available on NSG and other supercomputer resources, we can foster collaborations for using realistic network models to understand human cortical activity.

References

1.
Kudela P, Boatman-Reich D, Beeman D and Anderson WS. Modeling Neural Adaptation in Auditory Cortex. Front. Neural Circuits 2018, 05 Sept. https://doi.org/10.3389/fncir.2018.00072.
2.
Sivagnanam S, Majumdar A, Yoshimoto K, Astakhov V, Bandrowski A, Martone ME, Carnevale NT. Introducing the Neuroscience Gateway. IWSG, volume 993 of CEUR Workshop Proceedings 2013 CEUR-WS.org.
3.
Crone J, Boothe D, Yu A, Olie K, Franaszczuk P. Time step sensitivity in large scale compartmental models of the neocortex. BMC Neurosci 2018 19(Suppl 2):P184.

P47 Automated assessment and comparison of cortical neuron models

Justas Birgiolas¹, Russell Jarvis¹, Vergil Haynes², Richard Gerkin¹, Sharon Crook²

¹Arizona State University, School of Life Sciences, Tempe, United States of America; ²Arizona State University, School of Mathematical and Statistical Sciences, Tempe, AZ, United States of America

Correspondence: Sharon Crook (sharon.crook@asu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P47

Computational models are an indispensable tool for understanding the nervous system. However, describing, sharing, and re-using models with diverse components at many scales represents a major challenge in neuroscience. We have contributed to the development of the NeuroML model description standard [2] and the model sharing platform NeuroML-DB [1] to promote reproducibility and the re-use of data driven neuroscience models. We also have developed the SciDash framework for validating such models against experimental data [4] and sharing the validation outcomes for further scientific discovery at dash.scidash.org, increasing transparency and rigor in the field.

This infrastructure also supports automated pipelines for running large numbers of models shared in the NeuroML format at NeuroML-DB and characterization of these model neurons using simulated “experiments”. These experiments are based on the electrophysiology protocols used by the Allen Cell Type Database [3], which include square, long square, pink noise, ramp, short square and short square triple protocols, and are also the basis for model validation tests. Results are shared in interactive plots at NeuroML-DB. We have characterized over 1000 published cortical neuron models and used the electrophysiological properties of these cortical neuron models to cluster their dynamic behaviors and identify the biophysical properties of models that underlie these clusters. These properties are compared to similar results for experimentally-derived cortical neuron data, providing an overview of how well data-driven models represent the landscape of cortical neuron electrophysiology.

Acknowledgments: This research was funded in part by R01MH106674 from NIMH of the National Institutes of Health and R01EB021711 from NIBIB of the National Institutes of Health.

References

1.
Birgiolas J, et al. Ontology-assisted keyword search for NeuroML models. In Amarnath Gupta and Susan Rathbun, editors. Proceedings of the 27^th International Conference on Scientific and Statistical Database Management 2015. New York, NY: ACM; article 37.
2.
Gleeson P, et al. NeuroML: a language for describing data driven models of neurons and networks with a high degree of biological detail. PLoS Computational Biology 2010, 6, e1000815.
3.
Hawrylycz M, et al. Inferring cortical function in the mouse visual system through large-scale systems neuroscience. PNAS 2016, 113(27), 7337–44.
4.
Omar C, et al. Collaborative infrastructure for test-driven scientific model validation. In Companion Proceedings of the 36th International Conference on Software Engineering 2014 May 31 (pp. 524–527). ACM.

P48 High dimensional ion channel composition enables robust and efficient targeting of realistic regions in the parameter landscape of neuron models

Marius Schneider¹, Peter Jedlicka², Hermann Cuntz^3,4

¹University of Frankfurt, Institute for Physics, Butzbach, Germany; ²Justus Liebig University, Faculty of Medicine, Giessen, Germany; ³Frankfurt Institute for Advanced Studies (FIAS), Frankfurt am Main, Germany; ⁴Ernst Strüngmann Institute (ESI), Computational Neuroanatomy, Frankfurt am Main, Germany

Correspondence: Marius Schneider (marius-s@online.de)

BMC Neuroscience 2019, 20(Suppl 1):P48

Cellular and molecular sources of variability in the electrical activity of nerve cells are not fully understood. An improved understanding of this variability is the key to predict the response of nerve tissue to pathological changes. We have previously created a robust data-driven compartmental model of the hippocampal granule cell comprising 16 different ion channels and variable dendritic morphologies. Here, we show that it is possible to drastically reduce ion channel diversity while preserving the characteristic spiking behavior of real granule cells. In order to better understand the variability in spiking activity we generated large populations of validated granule cell models with different numbers of ion channels. Unreduced or less reduced models with a higher number of ion channels covered larger and more widely spread regions of the parameter landscape. Moreover, unreduced or less reduced models with a higher number of ion channels were more stable in the face of parameter perturbations. This suggests that ion channel diversity allows for increased robustness and higher flexibility of finding a solution in the complex parameter space. In addition to increasing our understanding of cell-to-cell variability, our models might be of practical relevance. Instead of a one-size-fits-all approach where a computer model simulates average experimental values, the population-based approach reflects the variability of experimental data and therefore might enable pharmacological studies in silico.

P49 Modelling brain folding using neuronal placement according to connectivity requirements

Moritz Groden¹, Marvin Weigand^2,3, Jochen Triesch³, Peter Jedlicka⁴, Hermann Cuntz^2,3

¹Justus Liebig University Giessen, Faculty of Medicine, Mannheim, Germany; ²Ernst Strüngmann Institute (ESI), Computational Neuroanatomy, Frankfurt am Main, Germany; ³Frankfurt Institute for Advanced Studies (FIAS), Neuroscience, Frankfurt am Main, Germany; ⁴Institute of Clinical Neuroanatomy Frankfurt, ICAR3R-Justus-Liebig University Giessen, Faculty of Medicine, Giessen, Germany

Correspondence: Moritz Groden (moritzgromail@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P49

Among different species of animals, the layout of the central nervous system varies extensively from individual clusters of neurons (ganglia) in invertebrates such as worms to solid brains found in mammals that typically exhibit increased folding the larger the animal. Such variations in layout may point to elemental differences in organization of circuitry and connectivity. However, many studies suggest that folding of the brain is a consequence of the restricted volume of the skull exerting mechanical forces on the cortex, which in turn folds to fit a larger surface area into such a confined cavity. In our study we consider a computational model that uses dimension reduction methods to ensure optimal placement of neurons, placing them according to connectivity needs, rather than modelling the forces exerted on the cortex. We assume a simple connectivity that features strong local but weak global (long-range) connections, which mimics the connectivity found in mammalian brains. The predictions made by our model cover all different phenotypes of brains found in animals, ranging from individual ganglia through smooth brains with no gyrification, to extremely convoluted brains for increasing cortical size. Many properties of the cortical morphology found in animals are reproduced by the model, which includes metrics such as the folding index and the fractal dimension. Our model presents a way to combine microscopic inter cellular connectivity with macroscopic morphologies into large-scale brain models that feature its neural network requirements.

P50 Dynamic neural field modeling of auditory categorization tasks

Pake Melland¹, Bob McMurray², Rodica Curtu¹

¹University of Iowa, Department of Mathematics, Iowa City, United States of America; ²University of Iowa, Psychological and Brain Sciences, Iowa City, United States of America

Correspondence: Rodica Curtu (rodica-curtu@uiowa.edu)

BMC Neuroscience 2019, 20(Suppl 1):P50

Categorization is the fundamental ability to treat distinct stimuli similarly; categorization applied to auditory stimuli is crucial for speech perception. For example, phonemes like “t” and “d” are categories that generalize across speakers and contexts. A fundamental question asks what mechanisms form the foundation for auditory category learning. We propose a dynamic neural network framework that combines plausible biological mechanisms and the theory of dynamic neural fields to model this process. The network models a task designed to emulate first language acquisition—a period of unsupervised learning followed by supervised learning. In the unsupervised phase the listener is presented with a sequence of pairs of tones; each pair corresponds to one of four categories defined by their frequencies. During this time the subject engages in a non-distracting task. Then the subject engages in a supervised task and is instructed to associate each tone-pair with a physical object representing one of the four auditory categories. Corrective feedback is given to the subject during the supervised learning. The mathematical model is used to manipulate mechanisms through which hypotheses can be made about the category learning process. We present preliminary results from model simulations of the experiment and compare them with implementations of the experiment on human subjects.

Network Description and Results. We propose a dynamic neural field composed of multiple layers allowing for the manipulation and testing of multiple locations of plasticity involved in the learning process. First, incoming sounds stimulate a one-dimensional tonotopically organized feature space composed of neural units that interact through local excitation with lateral inhibition. Units along this space are associated with sub-cortical auditory fields and respond to specific frequencies in order to capture physical properties of the stimuli. Activity in the feature space feeds forward through excitatory connections, which undergo depression with prolonged stimuli encounters, to regions of primary and secondary auditory cortex. Activity in these regions provide input to the category layer of the network composed of 4 neural units corresponding to the 4 categories defined in the task. These nodes are hypothesized to represent regions in auditory-related temporal cortical regions such as superior temporal gyrus [2] and the inferior frontal gyrus in humans, or the prefrontal cortex in rats [1]. In the theoretical network, the four category nodes are coupled through mutual inhibition and compete in a winner take all setting. Above threshold activation peaks in the category layer are interpreted as experimentally detectable responses. In the supervised portion of the task, synapses between auditory cortex nodes and category layer nodes are updated with via Hebbian processes with a reward/punishment parameter that serves as corrective feedback to the network. Parameters within the model are tuned so that responses in the category layer closely match behavioral results obtained from implementations of the experiment on human subjects that varied stimuli distributions, category prototypes, and category boundaries. The model predicts category learning at rates consistent with those found experimentally.

Acknowledgments: NSF CRCNS 151567.

References

1.
Francis NA, Winkowski DE, Sheikhattar A, Armengol K, Babadi B, Kanold PO. Small networks encode decision-making in primary auditory cortex. Neuron 2018 Feb 21;97(4):885–97.
2.
Mesgarani N, Cheung C, Johnson K, Chang EF. Phonetic feature encoding in human superior temporal gyrus. Science 2014 Feb 28;343(6174):1006–10.

P51 Role of TRP channels in temperature rate coding by drosophila noxious cold sensitive neurons

Natalia Maksymchuk, Akira Sakurai, Atit Patel, Nathaniel Himmel, Daniel Cox, Gennady Cymbalyuk

Georgia State University, Neuroscience Institute, Atlanta, GA, United States of America

Correspondence: Natalia Maksymchuk (nmaksymchuk1@gsu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P51

Noxious cold temperature can cause tissue damage and triggers protective behaviors of animals. Cellular mechanisms of noxious cold temperature coding are not well understood. We focus on Drosophila larval cold nociception capitalizing on a diverse array of approaches spanning genetics and animal behavior to electrophysiology and computational models. Larva responds to noxious cold by a well-characterized full-body contraction. Notably, this response is only triggered by a sufficiently fast temperature change. Class III (CIII) multidendritic sensory neurons and specific TRP channels are implicated in noxious cold temperature coding [1]. Based on Ca2+ imaging, specialized roles of Trpm and Pkd2 currents were established and our model explained an apparent paradox of these data [1, 2].

We performed electrophysiological recordings and Ca2+ imaging of CIII neurons along with behavioral analyses. We compared responses of wild type to slow and fast temperature changes from 24oC down to the 10oC. Cold-evoked contraction behavior was potentiated under fast ramping conditions relative to slow. Spiking and [Ca2+]i response at noxious cold were consistent with behavioral data. The CIII neurons exhibited a pronounced peak of spiking rate when the temperature was rapidly decreased and turned silent as the temperature was increased back to 24oC. The response was different when temperature changed slowly: the spiking rate was much smaller during the temperature decrease.

These results suggest that CIII neurons encode rate of temperature decrease. We hypothesize that inactivation processes of certain TRP channels could explain these differences. We focused on comparison of the roles of Pkd2 and Trpm currents as temperature sensors. Our computational model showed that the Ca2+-dependence of the Pkd2 inactivation constant could provide a mechanism of observed rate coding. This mechanism, implemented in the model, allowed us to reproduce recorded electrical activity data—high peak of firing rate in response to the rapid temperature change from 24oC to 10oC and silence during temperature return back to ambient levels. When the noxious cold temperature was held constant after fast ramp, Pkd2 channels inactivated, and low-frequency firing rate was supported through Trpm, responsible for coding temperature. This is consistent with behavioral data as well. In addition, the model shows that increased firing rate at fast temperature decline was accompanied by high [Ca2+]i level, whereas slow ramp resulted in significantly lower Ca2+. We conclude that certain TRP channels, such as Pkd2, could be responsible for high peak of firing rate at rapid temperature fall, whereas Trpm channels could encode the magnitude of temperature.

Acknowledgements: This work was supported by NIH R01 NS086082 and a GSU Brains & Behavior Seed Grant (DNC). NJH is a Brains and Behavior and Honeycutt Fellow; AAP is a 2CI Neurogenomics and Honeycutt Fellow.

References

1.
Turner HN, Armengol K, Patel AA, et al. The TRP Channels Pkd2, NompC, and Trpm Act in Cold-Sensing Neurons to Mediate Unique Aversive Behaviors to Noxious Cold in Drosophila. Current Biology 2016, 26(23), 3116–3128.
2.
Maksymchuk N, Patel AA, Himmel NJ, Cox DN, Cymbalyuk G. Modeling of TRP channel mediated noxious cold sensation in Drosophila sensory neurons. BMC Neuroscience 2018, 19(Suppl 2):64, 8–9.

P52 Role of Na+/K+ pump in dopamine neuromodulation of a mammalian central pattern generator

Alex Vargas, Gennady Cymbalyuk

Georgia State University, Neuroscience Institute, Atlanta, GA, United States of America

Correspondence: Alex Vargas (avarg453@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P52

CPGs are oscillatory neuronal circuits controlling rhythmic movements across vertebrates and invertebrates [1]. The Na/K pump contributes to the dynamics of bursting activity in variety of CPGs seen across species such as leech, tadpole, and mouse [2, 3, 4, 5, 6]. Movements like locomotion and heartbeat must be continually regulated for an animal to meet environmental and behavioral demands [3]. In vertebrate CPGs, dopamine has been shown to induce a range of subtle to pronounced effects on locomotory and other motor rhythms. Dopamine neuromodulation affects Na/K Pump, GIRK2-, A-, and h-currents through D1 and D2 receptors [7, 8]; this contributes to stabilization of CPG rhythmic activity. We developed a half-center oscillator (HCO) model of a spinal locomotor CPG, which comprises of four populations, two inhibitory and two excitatory. Under a certain parameter regime, the neurons are intrinsically bursting, utilizing a persistent-sodium current mechanism. We investigated activity regimes of single endogenously bursting neurons and HCO. In a range of high modulation level, we found stable periodic bursting, while within some range of low dopamine modulation levels, pronounced intermittent intrinsic patterns. We investigated the hypothesis that dopamine affects the network through activation of inward rectifying potassium currents, IGIRK and IA, and opposing changes of h-current all while interacting with pump current. The reduction in modulatory level of dopamine in the spinal locomotor CPG causes the model to transition from normal periodic bursting into intermittent bursting and then to silence. Our locomotor CPG model highlights the role of the pump and its co-modulation along with GIRK2-, A-, and h-currents in production of robust rhythmic output.

Acknowledgements: Supported by NINDS 1 R21 NS111355 to GC.

References

1.
Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiological reviews 1996 Jul 1;76(3):687–717.
2.
Picton LD, Zhang H, Sillar KT. Sodium pump regulation of locomotor control circuits. Journal of neurophysiology 2017 May 24;118(2):1070–81.
3.
Sharples SA, Whelan PJ. Modulation of rhythmic activity in mammalian spinal networks is dependent on excitability state. eNeuro 2017 Jan;4(1).
4.
Sharples SA, Humphreys JM, Jensen AM, et al. Dopaminergic modulation of locomotor network activity in the neonatal mouse spinal cord. Journal of neurophysiology 2015 Feb 4;113(7):2500–10.
5.
Kueh D, Barnett WH, Cymbalyuk GS, Calabrese RL. Na+/K+ pump interacts with the h-current to control bursting activity in central pattern generator neurons of leeches. eLife 2016 Sep 2;5:e19322.
6.
Tobin AE, Calabrese RL. Myomodulin increases I h and inhibits the Na/K pump to modulate bursting in leech heart interneurons. Journal of neurophysiology 2005 Dec;94(6):3938–50.
7.
Sharples SA, Whelan PJ. Modulation of rhythmic activity in mammalian spinal networks is dependent on excitability state. eNeuro 2017 Jan;4(1).
8.
Han P, Nakanishi ST, Tran MA, Whelan PJ. Dopaminergic modulation of spinal neuronal excitability. Journal of Neuroscience 2007 Nov 28;27(48):13192–204.

P53 Hypoxic suppression of Ca2+-ATPase pumps and mitochondrial membrane potential eliminates rhythmic activity of simulated interstitial cells of Cajal

Sergiy Korogod¹, Iryna Kulagina¹, Parker Ellingson², Taylor Kahl², Gennady Cymbalyuk²

¹Bogomoletz Institute of Physiology, National Academy of Sciences of Ukraine, Kiev, Ukraine; ²Georgia State University, Neuroscience Institute, Atlanta, GA, United States of America

Correspondence: Gennady Cymbalyuk (gcymbalyuk@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P53

Neonatal hypoxic-ischemic injury is a risk factor for necrotizing enterocolitis (NEC), an inflammatory bowel disease that is often associated with failures of gastrointestinal motility. This motility is driven by a pacemaker action of the interstitial cells of Cajal (ICCs) on intestinal smooth muscle cells (SMCs). The ICC pacemaker activity is determined by interplay of Ca2+channels, pumps, and exchangers present in the endoplasmic reticulum (ER), mitochondria and plasma membrane to form a characteristic Ca2+-handling mechanism. Ca2+-ATPase pumps in ICC are potential targets for injuring action of hypoxia as they operate by consuming energy stored in ATP due to oxidative phosphorylation in mitochondria. In an ICC model, we mimicked effects of hypoxia by reduction of the mitochondrial bulk membrane potential (ΔΨ*) or maximal rates of Ca2+-ATPase pumps in the plasmalemma or ER (PMCA or SERCA, respectively). ICC pacemaker activity (oscillations of the plasma membrane potential Emand intracellular calcium concentration [Ca2+]i) ceased by individual suppression of ΔΨ*, or PMCA, or SERCA and the cessation scenarios were case-specific. Since naturally hypoxia simultaneously affects all these actors, in this study, we explored scenarios of cessation of ICC pacemaker activity depending on combined suppression of ΔΨ*, PMCA, and SERCA. At fixed normal ΔΨ*, equal joint suppression of PMCA and SERCA dramatically reduced amplitude of [Ca2+]iand Emoscillations to “downstate” levels near their basal/rest values. This was similar to the effect of individual suppression of SERCA and dissimilar to that of PMCA, which was characterized by very low-amplitude oscillations about “upstate” levels of depolarized Emand elevated [Ca2+]i. In each case, changes in oscillations frequency were insignificant. Same suppression of PMCA and SERCA accompanied by that of ΔΨ*ceased the ICC pacemaker activity according to scenario observed during isolated reduction of ΔΨ*: the oscillations frequency reduced, duration of oscillatory plateaus of Emand [Ca2+]iextended and, at certain critically low ΔΨ*, the oscillations totally ceased and “downstate” basal [Ca2+]iand rest Emwere established.

Hence, hypoxic suppression of the above considered energy-producing and energy-consuming mechanisms in any combination led the cessation of ICC pacemaker activity and establishment of [Ca2+]iand Em“downstates” near their basal/rest levels without any or with very small oscillations. For the cessation scenario, the main governing factor was suppression of ΔΨ*, and among the Ca2+-ATPase pumps SERCA dominated over PMCA. The observed effects may have crucial pathological consequences for ICC-driven periodic contractions of electrically coupled SMCs manifested as gastrointestinal dysmotility and development of NEC. Since similar Ca2+-handling mechanisms operate in other type excitable cells, particularly in neurons, our model and protocols of computational experiments can be adapted for simulation studies of cellular mechanisms functional consequences of hypoxic injuries of the brain and spinal cord.

P54 Reconstruction and simulation of the cerebellar microcircuit: a scaffold strategy to embed different levels of neuronal details

Claudia Casellato¹, Alice Geminiani², Alessandra Pedrocchi², Elisa Marenzi¹, Stefano Casali¹, Chaitanya Medini¹, Egidio D’Angelo¹

¹University of Pavia, Dept. of Brain and Behavioral Sciences - Unit of Neurophysiology, Pavia, Italy; ²Politecnico di Milano, Department of Electronics, Information and Bioengineering, Milan, Italy

Correspondence: Claudia Casellato (claudia.casellato@unipv.it)

BMC Neuroscience 2019, 20(Suppl 1):P54

Computational models allow propagating microscopic phenomena into large-scale networks and inferencing causal relationships across scales. Here we reconstruct the cerebellar circuit by bottom-up modeling, reproducing the peculiar properties of this structure, which shows a quasi-crystalline geometrical organization well defined by convergence/divergence ratios of neuronal connections and by the anisotropic 3D orientation of dendritic and axonal processes [1].

Therefore, a cerebellum scaffold model has been developed and tested. It maintains scalability and can be flexibly handled to incorporate neuronal properties on multiple scales of complexity. The cerebellar scaffold includes the canonical neuron types: Granular cell, Golgi cell, Purkinje cell, Stellate and Basket cells, Deep Cerebellar Nuclei cell. Placement was based on density and encumbrance values, connectivity on specific geometry of dendritic and axonal fields, and on distance-based probability.

In the first release, spiking point-neuron models based on Integrate & Fire dynamics with exponential synapses were used. The network was run in the neural simulator pyNEST. Complex spatiotemporal patterns of activity, similar to those observed in vivo, emerged [2].

For a second release of the microcircuit model, an extension of the generalized Leaky Integrate & Fire model has been developed, optimized for each cerebellar neuron type and inserted into the built scaffold [3]. It could reproduce a rich variety of electroresponsive patterns with a single set of optimal parameters.

Complex single neuron dynamics and local connectome are key elements for cerebellar functioning.

Then, point-neurons have been replaced by detailed 3D multi-compartment neuron models. The network was run in the neural simulator pyNEURON. Further properties emerged, strictly linked to the morphology and the specific properties of each compartment.

This multiscale tool with different levels of realism has the potential to summarize in a comprehensive way the electrophysiological intrinsic neural properties that drive network dynamics and high-level behaviors.

The model, equipped with ad-hoc plasticity rules, has been embedded in a sensorimotor loop of EyeBlink Classical Conditioning. The network output evolved along repetitions of the task, therefore letting emerge three fundamental operations ascribed to the cerebellum: prediction, timing and learning of motor commands.

Acknowledgments: This research was supported by the HBP Neuroinformatics, Brain Simulation, and HPAC Platforms, funded by European Union’s Horizon 2020 under the Specific Grant Agreement No. 785907 (Human Brain Project SGA2), also involving the HBP Partnering Project CerebNEST.

References

1.
D’Angelo E, Antonietti A, Casali S, et al. Modeling the cerebellar microcircuit: new strategies for a long-standing issue. Frontiers in cellular neuroscience 2016 Jul 8;10:176.
2.
Casali S, Marenzi E, Medini KC, Casellato C, D‘Angelo E. Reconstruction and Simulation of a Scaffold Model of the Cerebellar Network. Frontiers in Neuroinformatics 2019;13:37.
3.
Geminiani A, Casellato C, Locatelli F, et al. Complex dynamics in simplified neuronal models: reproducing Golgi cell electroresponsiveness. Frontiers in Neuroinformatics 2018, 12, 1–19; https://doi.org/10.3389/fninf.2018.00088

P55 Simplified and physiologically detailed reconstructions of the cerebellar microcircuit

Elisa Marenzi¹, Chaitanya Medini¹, Stefano Casali¹, Martina Francesca Rizza¹, Stefano Masoli¹, Claudia Casellato², Egidio D’Angelo²

¹University of Pavia, Department of Brain and Behavioural Sciences, Pavia, Italy; ²University of Pavia, Dept. of Brain and Behavioral Sciences - Unit of Neurophysiology, Pavia, Italy

Correspondence: Elisa Marenzi (elisa.marenzi@unipv.it)

BMC Neuroscience 2019, 20(Suppl 1):P55

The cerebellum is the second largest cortical structure of the brain and contains about half of all brain neurons. Its modeling brings issues reflecting the peculiar properties of the circuit, which has a quasi-crystalline geometrical organization defined by convergence/divergence ratios of neuronal connections and by the anisotropic 3D orientation of dendritic and axonal processes [1]. A data-driven scaffold [2] comprising the granular (GrL), Purkinje (PL), molecular (ML) and Deep Cerebellar Nuclei (DCN) layers has been developed for testing network models with different complexities.

Its reconstruction follows sequential steps. Firstly, cells are placed in the simulation volume through an ad-hoc procedure: the GrL contains glomeruli (glom), granule cells (GrC) and Golgi cells (GoC); somata of Purkinje cells (PC) are in the PL while their dendritic trees are in the ML; here molecular layer interneurons (MLI)—stellate (SC) and basket cells (BC)—are placed whereas the DCN contains only the glutamatergic cells (DCNC).

The connectome stores the IDs of pre- and post-synaptic neurons. Parameters and morphological features derived from physiological experiments and literature data are the basis for its reconstruction, built on geometrical and probability-based rules. When using detailed neuronal morphologies, such rules have been improved to determine dendrites connected also through a touch detection algorithm.

The most typical behaviors of this microcircuit have been tested for both kinds of networks (pyNEST for the point-neuron version and pyNEURON when all detailed morphologies were available). Neuronal discharge of the different neuron populations in response to a mossy fiber burst have been evaluated, showing very similar results between the two simulators. In particular, GoC, SC and BC generate inhibitory bursts that contribute to terminate the GrC and PC bursts and to produce the burst-pause PC response.

Another important behavior regards the PC activation and sensitivity to molecular layer connectivity. The pattern of activity is determined by the various connection properties: particularly, PC inhibition is achieved through a differential orientation between SC and BC axons, while PC excitation depends on both ascending axons (aa) and pf synapses with specific origin from GrC. Their spatial extension reflects the propagation of activity through the MLI network.

The additional details introduced in pyNEURON simulations highlight more complex and physiologically relevant results that cannot be explained with a simplified model without dendrites. Moreover, the integration of the Inferior Olive completes the closed loop of the microcircuit, allowing to embed functional plasticity able to simulate learning processes.

Acknowledgements: The research was supported by the EU Horizon 2020 under the Specific Grant Agreements No. 720270 (HBP SGA1) and 785907 (HBP SGA2).

References

1.
D’Angelo E, Antonietti A, Casali S, et al. Modeling the cerebellar microcircuit: new strategies for a long-standing issue. Frontiers in cellular neuroscience 2016 Jul 8;10:176.
2.
Casali S, Marenzi E, Medini KC, Casellato C, D‘Angelo E. Reconstruction and Simulation of a Scaffold Model of the Cerebellar Network. Frontiers in neuroinformatics 2019;13:37.

P56 A richness of cerebellar granule cell discharge properties predicted by computational modeling and confirmed experimentally

Stefano Masoli¹, Marialuisa Tognolina¹, Francesco Moccia², Egidio D’Angelo¹

¹University of Pavia, Department of Brain and Behavioural Sciences, Pavia, Italy; ²University of Pavia, Department of Biology and Biotechnology “L. Spallanzani”, Pavia, Italy

Correspondence: Stefano Masoli (stefano.masoli@unipv.it)

BMC Neuroscience 2019, 20(Suppl 1):P56

The cerebellar granule cells (GrCs) are the most common neuron type in the central nervous system. Their highly packed distribution and misleading simple cytoarchitecture, generated the idea of a limited spike generation mechanism. The regular spikes discharge, recorded for short periods of time (<800ms), was the cornerstone for the simulation of realistic [1, 2]. We show that GrCs are capable of diverse patterns response when subjected to prolonged current inject (2s). The somato-dendritic sections were taken from [3], extend with a single section Hillock, an Axon Initial Segment (AIS), an ascending axon and two thin 1mm long parallel fibers. The ionic channels were taken from [1, 2, 4]. The Nav1.6 sodium channel was improved with FHF14 and located in the Hillock and AIS [5]. The calcium buffer was reworked to contain only Calretinin. The models, were automatically fitted with BluePyOpt/NEURON [6]. After 0.8-1s of regular firing, the models predicted three possible outcomes: 1) regular firing, 2) mild adaptation and 3) strong adaptation of firing. Patch-clamp experimental recordings (current-clamp configuration, parasagittal slices obtained from p18-24 Wistar rats) confirmed the modelling predictions on firing adaptation. In a subset of experiments GrCs showed firing acceleration that was not found by the optimization technique. To simulate these GrCs, a TRPM4 channel, known to mediate slow depolarizing currents, was linked to Calmodulin (Cam2C) concentration. This mechanism allowed to reach the accelerated state. These different firing properties impacted on synaptic excitation when the mossy fiber bundle was stimulated at different frequencies (1-100 Hz). Interestingly, a range of different filtering properties emerged, with some cells showing one-to-one responses while others responding faster or slower than the input. This modelling and experimental effort described GrCs properties that show the richness of their encoding capabilities.

Acknowledgements: This project has received funding from the Horizon 2020 Framework Programme for Research and Innovation under the Specific Grant Agreement No. 785907 (Human Brain Project SGA2).

References

1.
D’Angelo E, Nieus T, Maffei A, et al. Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow k+-dependent mechanism. Journal of Neuroscience 2001;21:759–70.
2.
Diwakar S, Magistretti J, Goldfarb M, Naldi G, D’Angelo E. Axonal Na+ channels ensure fast spike activation and back-propagation in cerebellar granule cells. Journal of Neurophysiology 2009;101:519–32.
3.
Masoli S, Rizza MF, Sgritta M, Van Geit W, Schürmann F, D’Angelo E. Single Neuron Optimization as a Basis for Accurate Biophysical Modeling: The Case of Cerebellar Granule Cells. Frontiers in cellular neuroscience 2017;11:1–14.
4.
Masoli S, Solinas S, D’Angelo E. Action potential processing in a detailed Purkinje cell model reveals a critical role for axonal compartmentalization. Frontiers in cellular neuroscience 2015;9:1–22.
5.
Dover K, Marra C, Solinas S, et al. FHF-independent conduction of action potentials along the leak-resistant cerebellar granule cell axon. Nature Communications 2016;7:12895.
6.
Van Geit W, Gevaert M, Chindemi G, et al. BluePyOpt: Leveraging Open Source Software and Cloud Infrastructure to Optimise Model Parameters in Neuroscience. Frontiers in Neuroinformatics 2016;10:1–30.

P57 Spatial distribution of Golgi cells inhibition and the dynamic geometry of Cerebellum granular layer activity: a computational study

Stefano Casali¹, Marialuisa Tognolina¹, Elisa Marenzi¹, Chaitanya Medini¹, Stefano Masoli¹, Martina Francesca Rizza¹, Claudia Casellato², Egidio D’Angelo¹

¹University of Pavia, Department of Brain and Behavioural Sciences, Pavia, Italy; ²University of Pavia, Department of Brain and Behavioural Sciences - Unit of Neurophysiology, Pavia, Italy

Correspondence: Stefano Masoli (stefano.masoli@unipv.it)

BMC Neuroscience 2019, 20(Suppl 1):P57

The cerebellum granular layer (GL) has been considered for a long time as a fine-grained spatio-temporal filter, characterized by its main role of delivering the right amount of information at the proper timing to the above molecular layer (ML) [1] While this general tenet remains, recent experimental and theoretical works suggest that the GL is endowed with a rich and complex variety of spatio-temporal dynamics, empowering the GL itself to exert a qualitatively strong influence upon the nature of the signal conveyed to the ML.

In the present work, a large-scale computational reconstruction of the GL network has been developed, exploiting previously published detailed single cell models of granule cells (GrCs, [2]) and Golgi cells [3]. The peculiar structure of synaptic connections has been observed and reproduced by means of geometrical-statistical connectivity rules derived from experimental data, when available [4]. One of the main features of GL connectivity, the anisotropic organization of GoCs axonal plexus, which is orthogonal to the parallel fibers (pfs, coronal axis) and runs along the parasagittal axis, plays a key role in shaping the spatio-temporal dynamics of GL activity. Excitatory / inhibitory ratio of GrCs response to external stimuli is organized in a center-surround structure, with excitation prevailing in the core and inhibition in the surround area [5] Simulations results show that Golgi cells inhibition is stronger along the parasagittal axis; these computational predictions have been confirmed by a set of experiments in acute slices in vitro with high resolution two-photon microscopy. This preferential path for Golgi cells inhibition can also affect how two simultaneously activated distant spots interact: simulations show that spots placed at a 100 or 200mm distance along the parasagittal axis can significantly inhibit each other; on the contrary, when the spots are positioned along the coronal axis, in line with the pfs, almost no interaction occurs. Specific synapses modulate the strength of this phenomenon; specifically, when the ascending axon (aa) synapses from GrCs to GoCs are switched-off, inhibitory interaction along the parasagittal axis decreases.

Acknowledgements: The research was supported by the EU Horizon 2020 under the Specific Grant Agreements No. 720270 (HBP SGA1) and 785907 (HBP SGA2).

References

1.
Rössert C, Dean P, Porril J. At the Edge of Chaos: How Cerebellar Granular Layer Network Dynamics Can Provide the Basis for Temporal Filters. PLoS Computational Biology 2015. 11(10). 1–28
2.
D’Angelo E, Nieus T, Maffei A, et al. Theta-frequency bursting and resonance in cerebellar granule cells: experimental evidence and modeling of a slow K+-dependent mechanism. Journal of Neuroscience 2001. 21. 759–770
3.
Solinas S, Forti L, Cesana E, et al. Fast-reset of pacemaking and theta-frequency resonance patterns in cerebellar Golgi cells: simulations of their impact in vivo. Frontiers in Cellular Neuroscience 2007. 1. 1–9
4.
Korbo L, Andresen BB, Ladefoged O, et al. Total numbers of various cell types in rat cerebellar cortex estimated using an unbiased stereological method. Brain Research 1993. 609. 262–268
5.
Mapelli J, D’Angelo E. The Spatial Organization of Long-Term Synaptic Plasticity at the Input Stage of Cerebellum. Journal of Neuroscience 2007. 27. 1285–1296

P58 Reconstruction and simulation of cerebellum granular layer functional dynamics with detailed mathematical models

Chaitanya Medini¹, Elisa Marenzi¹, Stefano Casali¹, Stefano Masoli¹, Claudia Casellato², Egidio D’Angelo²

¹University of Pavia, Department of Brain and Behavioural Sciences, Pavia, Italy; ²University of Pavia, Dept. of Brain and Behavioral Sciences - Unit of Neurophysiology, Pavia, Italy

Correspondence: Elisa Marenzi (elisa.marenzi@unipv.it)

BMC Neuroscience 2019, 20(Suppl 1):P58

Cerebellum has been widely known to be involved in several cognitive activities, however an elaborate investigation is required to validate known hypotheses and propose new theories. A detailed large-scale scaffold cerebellar circuit was developed with experimental connectivity rules on python NEURON with MPI configuration. An adaptable version of the cerebellar scaffold model [1] is developed on pyNEST and pyNEURON using morphologically-driven cell positions and functional connectivity, inspired from convergence/divergence geometry rules [2]. The reconstruction methodologies used for scaffold network improvises on the existing connectivity literature with Bounded Self-Avoiding Random Walk Algorithm. The simulations revealed a close correspondence to experimental results validating the network reconstruction. Simulations in pyNEURON gave results like those obtained with pyNEST. This is an important validation to ensure that the connectivity generates identical functional dynamics irrespective of the simulator platform. In the current study, pyNEURON scaffold cerebellar model has been extended from point neuron model network to detailed biophysical model network with similar connectome and positions. Detailed multicompartmental models of granule [3], Golgi, Purkinje [4], Stellate and Basket neurons (to be published) are being used for the study. As a first test case, the detailed neuron morphologies are connected using simpleneuronal connectivity rules representing spatially confined convergence/divergence rules. The number of synapses were evenly distributed along the dendritic length of these neuron models to compensate for the absence of computed distance probability between pre and post synaptic neurons. In the second case, a touch-detector based algorithm [5], was used to generate synaptic connectivity in the molecular layer (including Molecular Layer Interneurons and Purkinje Neurons). The network implementation is scalable and flexible to include new types of cell models or to replace the current version with updated models.

Acknowledgements: The research was supported by the EU Horizon 2020 under the Specific Grant Agreements No. 720270 (HBP SGA1) and 785907 (HBP SGA2).

References

1.
Casali S, Marenzi E, Medini KC, Casellato C, D‘Angelo E. Reconstruction and Simulation of a Scaffold Model of the Cerebellar Network. Frontiers in neuroinformatics 2019;13:37. https://doi.org/10.1101/532515
2.
Solinas S, Nieus T, D‘Angelo E. A realistic large-scale model of the cerebellum granular layer predicts circuit spatio-temporal filtering properties. Frontiers in cellular neuroscience 2010 May 14;4:12. https://doi.org/10.3389/fncel.2010.00012
3.
Diwakar S, Magistretti J, Goldfarb M, Naldi G, D’Angelo E. Axonal Na+ channels ensure fast spike activation and back-propagation in cerebellar granule cells. Journal of neurophysiology 2009 Feb;101(2):519-32. https://doi.org/10.1152/jn.90382.2008
4.
Masoli S, Solinas S, D’Angelo E. Action potential processing in a detailed Purkinje cell model reveals a critical role for axonal compartmentalization. Frontiers in cellular neuroscience 2015 Feb 24;9:47. https://doi.org/10.3389/fncel.2015.00047
5.
Reimann MW, King JG, Muller EB, Ramaswamy S, Markram H. An algorithm to predict the connectome of neural microcircuits. Frontiers in computational neuroscience 2015 Oct 8;9:28. https://doi.org/10.3389/fncom.2015.00120

P59 Reconstruction of effective connectivity in the case of asymmetric phase distributions

Azamat Yeldesbay¹, Gereon Fink², Silvia Daun²

¹University of Cologne, Institute of Zoology, Cologne, Germany; ²Research Centre Jülich, Institute of Neuroscience and Medicine (INM-3), Jülich, Germany

Correspondence: Azamat Yeldesbay (azayeld@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P59

The interaction of different brain regions is supported by transient synchronization between neural oscillations at different frequencies. Different measures based on synchronization theory are used to assess the strength of the interactions from experimental data, e.g. the phase-locking index, phase-locking value, phase-amplitude coupling, and cross-frequency coupling. Another approach measuring connectivity based on the reconstruction of the dynamics of phase interactions from experimental data was suggested by [3]. On the basis of this method and the theory of weakly coupled phase oscillators, [2] presented a variant of Dynamic Causal Modelling (DCM) for the analysis of phase-coupled data, where a Bayesian model selection and inversion framework is used to identify the structure and directed connectivity among brain regions from measured time series.

Most of the research on phase analysis relies on the direct association of the phases of the signals with the phases used in the theoretical description of weakly coupled oscillators. However, [1] showed that the phases of the signals measured in experiments are not uniquely defined and an asymmetric distribution of the measured phases (e.g. non-sine form of the signals) could result in a false estimation of the effective connectivity between the network nodes. Furthermore, [1] suggested a solution for this problem by introducing a transformation from an arbitrarily measured phase to a uniquely defined phase variable.

In this work we merge the ideas from the Dynamical Causal Modelling by [2] with the phase dynamics reconstruction by [1] and present a new modelling part that we implemented into DCM for phase coupling. In particular, we extended it with a distortion (a transformation) function that accommodates departures from purely sinusoidal oscillations.

By numerically analysing synthetic data sets with an asymmetric phase distribution, generated from models of coupled stochastic phase oscillators and coupled neural mass models, we demonstrate that the extended DCM for phase coupling with the additional modelling component correctly estimates the coupling functions that do not depend on the distribution of the observables.

The new proposed extension of DCM for phase coupling allows for different intrinsic frequencies among coupled neuronal populations, thereby making it possible to analyse effective connectivity between brain regions within and between different frequency bands, to characterize m:n phase coupling, and to unravel underlying mechanisms of the transient synchronization.

References

1.
Kralemann B, Cimponeriu L, Rosenblum M, Pikovsky A, Mrowka R. Phase dynamics of coupled oscillators reconstructed from data. Physical Review E. 2008 Jun 9;77(6):066205.
2.
Penny WD, Litvak V, Fuentemilla L, Duzel E, Friston K. Dynamic causal models for phase coupling. Journal of neuroscience methods 2009 Sep 30;183(1):19–30.
3.
Rosenblum MG, Pikovsky AS. Detecting direction of coupling in interacting oscillators. Physical Review E. 2001 Sep 21;64(4):045202.

P60 Movement related synchronization affected by aging: A dynamic graph study

Nils Rosjat, Gereon Fink, Silvia Daun

Research Centre Jülich, Institute of Neuroscience and Medicine (INM-3), Jülich, Germany

Correspondence: Nils Rosjat (n.rosjat@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P60

The vast majority of motor actions, including their preparation and execution, is the result of a complex interplay of various brain regions. Novel methods in computational neuroscience allow us to assess interregional interactions from time series acquired with in-vivo techniques like electro-encephalography (EEG). However, our knowledge of the functional changes in neural networks during non-pathological aging is relatively poor.

To advance our knowledge on this topic, we recorded EEG (64 channels) from 18 right-handed healthy younger subjects (YS, 22–35 years) and 24 right-handed healthy older subjects (OS, 60–79 years) during a simple motor task. The participants had to execute visually-cued low frequency left or right index finger tapping movements. Here, we used the relative phase-locking value (rPLV) [1] to examine whether there is an increase in functional coupling of brain regions during this simple motor task. We analyzed the connectivity for 42 electrodes focusing on connections between electrodes lying above the ipsi- and contralateral premotor and sensorimotor areas and the supplementary motor area.

Widely used approaches for network definition are based on certain functional connectivity measures (e.g. similarity in BOLD time series, phase locking, coherence). These methods typically focus on constructing a single network representation over a fixed time period. However, this approach cannot make use of the high temporal resolution of EEG data and is not able to shed light on the understanding of temporal network dynamics. Here we used graph theory-based metrics that were developed in the last several years that can deal with the analysis of temporally evolving network structures [2].

Our rPLV network analysis revealed four major results: An underlying coupling structure around movement onset in the low frequencies (2–7 Hz) that is present in YS and OS. The network in OS involved several additional connections and showed an overall increased coupling structure (Fig. 1). While the motor related networks of YS mainly involved ipsilateral frontal, contralateral frontal and central electrodes and interhemispheric pairs of electrodes connecting frontal ipsilateral with central contralateral ones, the networks of OS showed especially an increased interhemispheric connectivity. The analysis of hub nodes and communities showed a strong involvement of occipital, parietal, sensorimotor and central regions in YS. While the networks of OS involved similar hub nodes, the first occurrence of sensorimotor regions was clearly delayed and central electrodes played a more important role in the network (Fig. 1). Moreover, the motor related node degrees were significantly increased in OS.

In addition to previously published results [3, 4], we were able to unravel the time-development of specific age-related dynamic network structures that seem to be a necessary prerequisite for the execution of a motor act. The increased interhemispheric connectivity of frontal electrodes fits very well to previous fMRI literature reporting an overactivation in frontal regions in older subjects. Our results also hint at a loss of lateralization via increased connectivity in both hemispheres as well as interhemispheric connections.

References

1.
Lachaux JP, Rodriguez E, Martinerie J, Varela FJ. Measuring phase synchrony in brain signals. Human brain mapping 1999, 8(4), 194–208.
2.
Sizemore AE, Bassett DS. Dynamic graph metrics: Tutorial, toolbox, and tale. NeuroImage 2018, 180, 417-427.
3.
Dennis NA, Cabeza R. Neuroimaging of healthy cognitive aging. The handbook of aging and cognition 2008, 3, 1-54.
4.
Cabeza R. Hemispheric asymmetry reduction in older adults: the HAROLD model. Psychology and aging 2002, 17(1), 85.

P61 How a scale-invariant avalanche regime is responsible for the hallmarks of spontaneous and stimulation-induced activity: a large-scale model

Etienne Hugues, Olivier David

Université Grenoble Alpes, Grenoble Institut des Neurosciences, Grenoble, France

Correspondence: Etienne Hugues (etienne.hugues@upf.edu)

BMC Neuroscience 2019, 20(Suppl 1):P61

At rest, BOLD fMRI and MEG recordings have revealed the existence of functional connectivity (FC) [1] and of scale-invariant neural avalanches [2], respectively. Under stimulation, neural activity is known to propagate on the brain network and, across trials, firing variability is found to be generically reduced [3]. Understanding the properties of the spontaneous state emerging on the brain network, together with its modifications during stimulation is a fundamental problem in neuroscience, still largely untouched.

A large-scale modeling approach, where the brain network is modeled by local neuronal networks connected through the large-scale connectome, has been previously used. Assuming that the whole brain is in an asynchronous state, the noisy fluctuations reverberating on the network have been found to be responsible for BOLD FC. However, in this fluctuation scenario, stimulation-induced activity is strongly damped while propagating on the network, even when trying to correct for this limitation [4].

We show that low spontaneous firing prevents neural activity to propagate in the fluctuation scenario. Adding neural adaptation, a local node can have two dynamical states, allowing the network dynamics to escape from the fluctuation regime, through brief excursions of individual nodes towards the higher activity state, allowing neural activity to effectively propagate on the network.

In the spontaneous state, the model exhibits neural avalanches, whose size distribution is scale-invariant for some global coupling strength value. BOLD FC is found to originate from the avalanches, therefore from nonlinear dynamics. The best agreement with empirical BOLD FC is found for scale-invariant avalanches.

Stimulation tends to entrain some nodes towards the high activity state, eliciting a reproducible propagation on the network, which simultaneously leads to a decrease of neural variability compared to the spontaneous state where more fluctuations occur, attributing a global origin to this phenomenon. Finally, neural activity is found to propagate optimally in the scale-invariant avalanche regime.

In conclusion, this study demonstrates that, beyond the brain connectome, a spontaneous state in the scale-invariant avalanche regime is crucial to reproduce the hallmarks of spontaneous and stimulation-induced activity. Neural variability decreases wherever activity propagates reliably, going beyond experimental results [3] and previously proposed mechanisms. Overall, the present work proposes a unified theory of the large-scale brain dynamics for a wide range of experimental findings.

Acknowledgments: We thank the European Research Council for supporting E.H. and O.D. with E.U.’s 7th Framework Programme / ERC Grant 616268 “F-TRACT”.

References

1.
Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nature Reviews Neuroscience 2007, 8, 700–711.
2.
Shriki O, Alstott J, Carver F, et al. Neuronal avalanches in the resting MEG of the human brain. Journal of Neuroscience 2013, 33, 7079–7090.
3.
Churchland MM, Yu BM, Cunningham JP, et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nature Neuroscience 2010, 13, 369–378.
4.
Joglekar MR, Mejias JF, Yang GR, et al. Inter-areal balanced amplification enhances signal propagation in a large-scale circuit model of the primate cortex. Neuron 2018, 98, 222–234.

P62 Astrocytes restore connectivity and synchronization in dysfunctional cerebellar networks

Paolo Bonifazi¹, Sivan Kanner², Miri Goldin¹, Ronit Galron², Eshel Ben Jacob³, Ari Barzilai², Maurizio De Pitta’⁴

¹Biocruces Health Research Institute, Neurocomputational imaging, Bilbao, Spain; ²Tel Aviv University, Department of Neurobiology, Tel Aviv, Israel; ³Tel Aviv University, School of Physics and Astronomy, Tel Aviv, Israel; ⁴Basque Center for Applied Mathematics: BCAM, Bilbao, Spain

Correspondence: Paolo Bonifazi (paol.bonifazi@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P62

In the last two decades, it has become appreciated that glial cells play a critical role in brain degenerative diseases (BDDs). The symptoms of BDDs arise from pathological changes to neuro-glia interactions, leading to neuronal cell death, disrupted neuro-glia communication, and impaired cell function, all of which affect global dynamics of brain circuitry. Astrocytes, a particular glial cell type, play key roles in regulating pathophysiology of neuronal functions. In this work, we tested the hypothesis that neuronal circuit dynamics were impacted as a consequence of disrupted neuron-astrocyte physiology in a mouse model of the BDD that results from a deficiency in the ATM protein. The gene encoding ATM is mutated in the human genetic diseaseAtaxia-Telangiectasia (A-T). One of the most devastating symptoms of A-T is the cerebellar ataxia, with significant loss of Purkinje and granule neurons in the cerebellum, that leads progressively to general motor dysfunction. We used primary cerebellar cultures grown from postnatal wild-type (WT) and Atm −/− mice to study how ATM deficiency influences the structure and dynamics of cerebellar neuronal-astrocyte circuits. We hypothesized that ATMdeficiency impairs the neuronal-astrocytic interactions underlying spontaneous neuronal synchronizations, a hallmark activity pattern of the developing nervous system.

We report that the absence of Atm in neurons and astrocytes severely alters astrocyte morphology and the number of pre- and post-synaptic puncta, disrupting the topology and dynamics of cerebellar networks. Functionally, Atm −/− networks showed a reduced number of global synchronizations (GSs) which recruited the whole imaged neuronal population, in favor of an increased number of sparse synchronizations (SSs), where only a small subset of neurons of the network fired in together. Structurally, higher numbers of synaptic puncta in Atm−/−networks relative to numbers in wild-type cultures were associated with lower levels of autophagy. These reported structural and functional anomalies were all rescued in chimeric neuronal networks composed of Atm−/−neurons and WT astrocytes. In contrast, cultures of WT neurons with Atm−/−astrocytes led to significant neuronal cell death. Characterizations of adult Atm−/−cerebella similarly showed disrupted astrocyte morphology, upregulated GABAergic markers, and dysregulated mTOR-mediated signaling and autophagy.

The apparent contradiction between a larger number of synapses in the Atm−/−circuits and lower occurrence of network synchronizations could result from the presence of non-functional connections (aborted functional connectivity hypothesis) or from the homeostatic downscaling of synaptic weights between neurons (aborted effective connectivity hypothesis). We explore the latter hypothesis extrapolating on its possible consequences on in-vivo cerebellar dynamics. With this regard we presenta spiking neural network model for the above described in-vitro experiments, where increase in connectivity in parallel withscaling of synaptic weightscan account for the increase of SSs in the KO model. Next, we consider the same increase in connectivity yet in relation to GABAergic transmission in a simplified model of cerebellar circuits and we show that an increase of inhibitory connections results in a reduction of functional connections in evoked excitatory activity, suggesting disrupted sensory and motor processing cascade in ataxia.

P63 Pybrep: Efficient and extensible software to construct an anatomical basis for a physiologically realistic neural network model

Ines Wichert¹, Sanghun Jee², Sungho Hong³, Erik De Schutter³

¹Champalimaud Center for the Unknown, Champalimaud Research, Lisbon, Portugal; ²Korea University, College of Life Science and Biotechnology, Seoul, South Korea; ³Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Okinawa, Japan

Correspondence: Sungho Hong (shhong@oist.jp)

BMC Neuroscience 2019, 20(Suppl 1):P63

In building a physiologically realistic model of a neural network, one of the first challenges is to determine the positions of neurons and their mutual connectivity based on their anatomic features. Recent studies have shown that cell locations are often distributed in non-random spatial patterns [1–3]. Also, synaptic and gap junction-mediated connectivity is constrained by the spatial geometry of axonal and dendritic arbors. These features have to be taken into account for realistic modeling since they determine convergence/divergence of the input/output of the neurons, respectively, and fundamentally impact their spatiotemporal activity patterns [4,5].

Here we present pybrep, an easily usable and extendable Python tool, designed for efficient generation of cell positions and connectivity based on anatomical data in large neuronal networks, and demonstrate its successful application to our previously published network model of the cerebellar cortex [5] and its extension. In a first step, pybrep generates cell positions by the Poisson disk sampling algorithm [6]: By sampling quasi-random points in a space with a constraint on their mutual distances, it simulates tight packing of spherical cells with given radii. We adapted this to generate multiple cell types sequentially and apply coordinate transformations to compensate for anisotropic geometry. Based on those locations, it generates point clouds representing specified axonal and dendritic morphologies. Using an efficient nearest neighbor search algorithm, it then identifies candidate connections by finding points that satisfy a distance condition. This can be done in 3D, or in some cases even more efficiently with a 2D projection method that exploits morphological regularities such as the long parallel fibers in the cerebellar network.

In the setup process for the cerebellar cortex model, pybrep efficiently produced the positions of more than a million cellular structures, including granule and Golgi cells as well as mossy fiber glomeruli, based on existing data about densities, volume ratios, etc. [7] Notably, applying a physiologically plausible, distance-based connection rule to the generated positions reproduced the well-known 4-to-1 connectivity between glomeruli and granule cells [7]. Pybrep also generated synaptic connectivity, particularly between the granule and Golgi cells, by an order of magnitude faster compared to our previous software for the same task [5]. Finally, the modular structure of pybrep allowed for an easy extension of the existing model by adding a new cell type, the molecular layer interneuron.

Pybrep depends only on a few external packages, but can easily be combined with existing Python tools, such as those for parallelization and scaling-up. These features will make pybrep a useful tool for constructing diverse network models in various sizes.

References

1.
Töpperwien M, van der Meer F, Stadelmann C, Salditt T. Three-dimensional virtual histology of human cerebellum by X-ray phase-contrast tomography. PNAS 2018 Jul 3;115(27):6940–5.
2.
Jiao Y, Lau T, Hatzikirou H, Meyer-Hermann M, Corbo JC, Torquato S. Avian photoreceptor patterns represent a disordered hyperuniform solution to a multiscale packing problem. Physical Review E 2014 Feb 24;89(2):022721.
3.
Haruoka H, Nakagawa N, Tsuruno S, Sakai S, Yoneda T, Hosoya T. Lattice system of functionally distinct cell types in the neocortex. Science 2017 Nov 3;358(6363):610–5.
4.
Rosenbaum R, Smith MA, Kohn A, Rubin JE, Doiron B. The spatial structure of correlated neuronal variability. Nature neuroscience 2017 Jan;20(1):107.
5.
Sudhakar SK, Hong S, Raikov I, et al. Spatiotemporal network coding of physiological mossy fiber inputs by the cerebellar granular layer. PLoS computational biology 2017 Sep 21;13(9):e1005754.
6.
Bridson R. Fast Poisson disk sampling in arbitrary dimensions. In SIGGRAPH sketches 2007 Aug 5 (p. 22).
7.
Billings G, Piasini E, Lőrincz A, Nusser Z, Silver RA. Network structure within the cerebellar input layer enables lossless sparse encoding. Neuron 2014 Aug 20;83(4):960–74.

P64 3D modeling of complex spike bursts in a cerebellar Purkinje cell

Alexey Martyushev¹, Erik De Schutter²

¹Okinawa Institute of Science and Technology (OIST), Erik De Schutter Unit, Onna-son, Okinawa, Japan; ²Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Onna-Son, Japan

Correspondence: Alexey Martyushev (martyushev.alexey@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P64

The cerebellum regulates motor movements through the function of its Purkinje neurons. Purkinje neurons generate electrophysiological activity in the form of firing simple (fast) and complex (slow) spikes differing in the number of spikes, amplitude and duration. The interest in studying the complex spike bursts is based on their role in controlling and learning human body movements.

This study describes a new version of the recently published spatial single Purkinje cell model implemented in the NEURON simulation software by [1]. This model uses a variety of ionic mechanisms to generate simple and complex spike activity. We analyze the difference in modeling results between the NEURON [2] and the Stochastic Engine for Pathway Simulation (STEPS) [3] simulation environments. The NEURON modeling approach idealizes the complex 3D morphology as cylinders (>10 µm scale) with uniform membrane properties and considers only 1D membrane potential propagation, while STEPS treats the neuron morphology in the form of a more detailed (<1 µm scale) tetrahedral 3D mesh [3]. These differences affect channel properties and calcium dynamics in the Purkinje cell model. Additionally, the need of detailed neuronal modeling leverages the increase of using electron microscopy to provide super resolution neuronal reconstructions.

The results of this study will detail our understanding of intrinsic properties and functioning of neurons at the nanoscale. Possible differences between the two software tools may require us to reconsider our approaches to computational modelling of the neuronal activity in the brain [4].

References

1.
Zang Y, Dieudonne S, De Schutter E. Voltage- and Branch-Specific Climbing Fiber Responses in Purkinje Cells. Cell Rep. 2018, 24(6), p. 1536–1549.
2.
Carnevale NT, Hines M. The NEURON Book. Cambridge, UK: Cambridge University Press; 2006.
3.
Hepburn I, et al. STEPS: efficient simulation of stochastic reaction-diffusion models in realistic morphologies. BMC Syst Biol. 2012, 6, p. 36.
4.
Chen W, De Schutter E. Time to Bring Single Neuron Modeling into 3D. Neuroinformatics 2017, 15, p. 1–3.

P65 Hybrid modelling of vesicles with spatial reaction-diffusion processes in STEPS

Iain Hepburn, Sarah Nagasawa, Erik De Schutter

Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Onna-son, Japan

Correspondence: Iain Hepburn (ihepburn@oist.jp)

BMC Neuroscience 2019, 20(Suppl 1):P65

Vesicles play a central role in many fundamental neuronal cellular processes. For example, pre-synaptic vesicles package, transport and release neurotransmitter, and post-synaptic AMPAR trafficking is controlled by the vesicular-endosomal pathway. Therefore, vesicle trafficking underlies crucial brain features such as the dynamics and strength of chemical synapses, yet vesicles have only received limited attention in computational neuronal modelling to now.

Molecular simulation software STEPS (steps.sourceforge.net) applies reaction-diffusion kinetics on realistic tetrahedral mesh structures by tracking the molecular population within tetrahedrons and modelling their local interactions stochastically. STEPS is usually applied to subcellular models such as synaptic plasticity pathways and so is a natural choice for extension to vesicle processes. However, combining vesicle modelling with mesh-based reaction-diffusion modelling poses a number of challenges.

The fundamental issue to solve is the interaction between spherical vesicle objects and the tetrahedral mesh. We apply an overlap library and track local vesicle-tetrahedron overlap, which allows us to modify local diffusion rates and model interactions between vesicular surface proteins and molecules in the tetrahedral mesh such as cytosolic and plasma membrane proteins as the vesicles sweep through the mesh. These interactions open up many modelling applications such as vesicle-endosome interaction, membrane-docking, priming and neurotransmitter release, all solved to a high level of spatial and biochemical detail.

This hybrid modelling, that includes dynamic vesicle processes and dependencies, presents challenges in ensuring accuracy whilst maintaining efficiency of the software, and this is an important focus of our work. Where possible we validate the accuracy of our modelling processes, for example by validating diffusion and binding rates. Optimisation efforts are ongoing but we have had some successes, for example by applying local updates to the dynamic vesicle processes.

We apply this new modelling technology to the post-synaptic AMPAR trafficking pathway. AMPA receptors undergo clatherin-dependent endocytosis and are trafficked to the endosome where they are sorted for either degradation or returned to the membrane via recycling vesicles. Rab GTPases coordinate sorting through the endosomal system.

Due to our new hybrid modelling technology it is possible to simulate this pathway, as well as potentially other areas of cell biology where vesicle trafficking and function play an important role, to high spatial detail. We hope that our current efforts and future additions open up new avenues of modelling research in neuroscience.

P66 A computational model of social motivation and effort

Ignasi Cos¹, Gustavo Deco²

¹Pompeu Fabra University, Center for Brain & Cognition, Barcelona, Spain; ²Universitat Pompeu Fabra, Barcelona, Spain

Correspondence: Ignasi Cos (ignasi.cos@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P66

Although the relationship between motivation and behaviour has been extensively studied, the specifics of how motivation relates to movement and how effort is considered to select specific movements remains largely controversial. Indeed, moving towards valuable states implies investing a certain amount of effort and coming up with appropriate motor strategies. How are these principles modulated by social pressure?

To investigate whether and how motor parameters and decisions between movements were influenced by differentially induced motivated states, we performed a decision-making paradigm where healthy human participants made choices between reaching movements under different conditions. Their goal was to accumulate reward by selecting one of two reaching movements of opposite motor cost, and to perform the selected reaching movement. Reward was contingent upon target arrival precision. All trials had fixed duration to prevent the participants from maximizing reward by minimizing temporal discount.

We manipulated the participants’ motivated state via social pressure. Each experimental session was composed of six blocks, during which subjects could either play alone or accompanied by a simulated co-player. Within this illusion, the amount of reward obtained by the participant and by their companion was reported at the end of each trial. The previous ten trial ranking for the two players was shown briefly every nine trials. However, no specific mention to competition was ever made to the subjects in the instruction, and any such mention reported by the participant was immediately rejected by the experimenter.

The results show that participants increased precision alongside the skill of their co-actor, implying that the participants cared about their own performance. The main behavioural result was an increase of the movement duration between baseline (playing alone) and any other condition (with any co-actor), and a modulation of amplitude as the skill of the co-actor became unattainable. As to provide a quantitative account of the dynamics of social motivation, we developed a generative computational model of decision-making and motor control, based on the optimization of the trade-off between the benefits and costs associated to a movement. Its predictions show that this optimization depends on the motivational context where the movements and the choices between them are performed. Although further research remains to be performed to understand the specific intricacies of this relationship between motor control theory and motivated states, this suggests that this inter-relation between internal physiological dynamics and motor behaviour is more than a simple modulation of the vigour of movement.

Acknowledgements: This project was funded by the Marie Sklodowska-Curie Research Grant Scheme (grant number IF-656262).

P67 Functional inference of real neural networks with artificial neural networks

Mohamed Bahdine¹, Simon V. Hardy², Patrick Desrosiers³

¹Laval University, Quebec, Canada; ²Laval University, Département d’informatique et de génie logiciel, Quebec, Canada; ³Laval University, Département de physique, de génie physique et d’optique, Quebec, Canada

Correspondence: Mohamed Bahdine (mohamed.bahdine.1@ulaval.ca)

BMC Neuroscience 2019, 20(Suppl 1):P67

Fast extraction of connectomes from whole-brain functional imaging is computationally challenging. Despite the development of new algorithms that efficiently segment the neurons in calcium imaging data, the detection of individual synapses in whole-brain images remains intractable. Instead, connections between neurons are inferred using time series that describe the evolution of neurons’ activity. We compare classical methods of functional inference such as Granger Causality (GC) and Transfer Entropy (TE) to deep learning approaches such as Convolutional Neural Networks (CNN) and Long Short-Term Memory (LSTM).

Since ground truth is required to compare the methods, synthetic time series are generated from the C. Elegans’ connectome using the leaky-integrate and fire neuron model. Noise, inhibition and adaptation are added to the model to promote richer neuron activity. To mimic typical calcium-imaging data, the time series are down-sampled from 10 kHz to 30 Hz and filtered with calcium and fluorescence dynamics. Additionally, we produce multiple simulations by varying brain and stimulation parameters to test each inference methods on different types of brain activity.

By comparing the mean ROC curves of each method (see Fig. 1) we find that the CNN outperforms all other methods up to a false positive rate of 0.7, while GC has the weakest performance, being on average slightly above random guesses. TE performs better than LSTM for low false positive rates, but these performances are inverted for false positive rates higher than 0.5. Although the CNN has the highest mean curve, it also has the largest width, meaning the CNN is the most variable and therefore least consistent inference method. TE’s mean ROC curve’s width is significantly narrower than other methods for low false positive rates and slowly grows when it meets other curves. The choice of an inference method is therefore dependant on one’s tolerance to false positives and variability.

P68 Stochastic axon systems: A conceptual framework

Skirmantas Janusonis¹, Nils-Christian Detering²

¹University of California, Santa Barbara, Department of Psychological and Brain Sciences, Santa Barbara, CA, United States of America; ²University of California, Santa Barbara, Department of Statistics and Applied Probability, Santa Barbara, CA, United States of America

Correspondence: Skirmantas Janusonis (janusonis@ucsb.edu)

BMC Neuroscience 2019, 20(Suppl 1):P68

The brain contains many “point-to-point” projections that originate in known anatomical locations, form distinct fascicles or tracts, and terminate in well-defined destination sites. This “deterministic brain” coexists with the “stochastic brain,” the axons of which disperse in meandering trajectories, creating meshworks in virtually all brain nuclei and laminae. The cell bodies of this system are typically located in the brainstem, as a component of the ascending reticular activating system (ARAS). ARAS axons (fibers) release serotonin, dopamine, norepinephrine, acetylcholine, and other neurotransmitters that regulate perception, cognition, and affective states. They also play major roles in human mental disorders (e.g., Major Depressive Disorder and Autism Spectrum Disorder).

Our interdisciplinary program [1, 2] seeks to understand at a rigorous level how the behavior of individual ARAS fibers determines their equilibrium densities in brain regions. These densities are commonly used in fundamental and applied neuroscience and can be thought to represent a macroscopic measure that has a strong spatial dependence (conceptually similar to temperature in thermodynamics). This measure provides essential information about the environment neuronal ensembles operate in, since ARAS fibers are present in virtually all brain regions and achieve extremely high densities in many of them.

A major focus of our research is the identification of the stochastic process that drives individual ARAS trajectories. Fundamentally, it bridges the stochastic paths of single fibers and the essentially deterministic fiber densities in the adult brain. Building upon state-of-the-art microscopic analyses and theoretical models, the project investigates whether the observed fiber densities are the result of self-organization, with no active guidance by other cells. Specifically, we hypothesize that the knowledge of the geometry of the brain, including the spatial distribution of physical “obstacles” in the brain parenchyma, provides key information that can be used to predict regional fiber densities.

In this presentation, we focus on serotonergic fibers. We demonstrate that a step-wise random walk, based on the von Mises-Fisher (directional) probability distribution, can provide a realistic and mathematically concise description of their trajectories in fixed tissue. Based on the trajectories of serotonergic fibers in 3D-confocal microscopy images, we present estimates of the concentration parameter (κ) in several brain regions with different fiber densities. These estimates are then used to produce computational simulations that are consistent with experimental results. We also propose that other stochastic models, such as the superdiffusion regime of the Fractional Brownian Motion (FBM), may lead to a biologically accurate and analytically rich description of ARAS fibers, including their temporal dynamics.

Acknowledgements: This research is funded by the National Science Foundation (NSF 1822517), the National Institute of Mental Health (R21 MH117488), and the California NanoSystems Institute (Challenge-Program Development Grant).

References

1.
Janusonis S, Detering N. A stochastic approach to serotonergic fibers in mental disorders. Biochimie 2018, in press.
2.
Janusonis S, Mays KC, Hingorani MT. Serotonergic fibers as 3D-walks. ACS Chem. Neurosci. 2019, in press.

P69 Replicating the mouse visual cortex using Neuromorphic hardware

Srijanie Dey, Alexander Dimitrov

Washington State University Vancouver, Mathematics and Statistics, Vancouver, WA, United States of America

Correspondence: Srijanie Dey (srijanie.dey@wsu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P69

The primary visual cortex is one of the most complex parts of the brain offering significant modeling challenges. With the ongoing development of neuromorphic hardware, simulation of biologically realistic neuronal networks seems viable. According to [1], Generalized Leaky Integrate and Fire Models (GLIFs) are capable of reproducing cellular data under standardized physiological conditions. The linearity of the dynamical equations of the GLIFs also work to our advantage. In an ongoing work, we proposed the implementation of five variants of the GLIF model [1], incorporating different phenomenological mechanisms, into Intel’s latest neuromorphic hardware, Loihi. Owing to its architecture that supports hierarchical connectivity, dendritic compartments and synaptic delays, the current LIF hardware abstraction in Loihi is a good match to the GLIF models. In spite of that, precise detection of spikes and the fixed-point arithmetic on Loihi pose challenges. We use the experimental data and the classical simulation of GLIF as references for the neuromorphic implementation. Following the benchmark in [2], we use various statistical measures on different levels of the network to validate and verify the neuromorphic network implementation. In addition, variance among the models and within the data based on spike times are compared to further support the network’s validity [1, 3]. Based on our preliminary results, viz., implementation of the first GLIF model followed by a full-fledged network in the Loihi architecture, we believe it is highly probable that a successful implementation of a network of different GLIF models could lay the foundation for replicating the complete primary visual cortex.

References

1.
Teeter C, Iyer R, Menon V, et al. Generalized leaky integrate-and-fire models classify multiple neuron types. Nature communications 2018 Feb 19;9(1):709.
2.
Trensch G, Gutzen R, Blundell I, Denker M, Morrison A. Rigorous neural network simulations: a model substantiation methodology for increasing the correctness of simulation results in the absence of experimental validation data. Frontiers in Neuroinformatics 2018;12.
3.
Paninski L, Simoncelli EP, Pillow JW. Maximum likelihood estimation of a stochastic integrate-and-fire neural model. Advances in Neural Information Processing Systems 2004; pp 1311–1318.

P70 Understanding modulatory effects on cortical circuits through subpopulation coding

Matthew Getz¹, Chengcheng Huang², Brent Doiron²

¹University of Pittsburgh, Neuroscience, Pittsburgh, PA, United States of America; ²University of Pittsburgh, Mathematics, Pittsburgh, United States of America

Correspondence: Matthew Getz (mpg39@pitt.edu)

BMC Neuroscience 2019, 20(Suppl 1):P70

Information theoretic approaches have shed light on the brain’s ability to efficiently propagate information along the cortical hierarchy, as well as exposed limitations in this process. One common measure of coding capacity, linear Fisher Information (FI), has also been used to study the neural code within a given cortical region. In particular, we recently used this approach to study the effects of an attention-like modulation on a cortical population model [1]. Previous studies have been largely agnostic as to the class of neuron that encodes a particular sensory variable, assuming little more than stimulus tuning properties. While it is widely accepted that local cortical dynamics involve an interplay between excitatory and inhibitory neurons, there are a large number of anatomical studies showing that excitatory neurons are the dominant projection neurons from one cortical area to the next. This suggests that, rather than maximizing the FI across the full excitatory and inhibitory network, to improve down-stream readout of neural codes the goal of top-down modulation may instead be to modulate the information carried only within the excitatory population, denoted FI-E [1]. In this study we explore this hypothesis using a combined numerical and analytic analysis of population coding in simplified model cortical networks.

We first study this effect in a recurrently coupled, excitatory (E)/inhibitory (I) population pair coding for a scalar stimulus variable (Fig. 1, A). We demonstrate that while the FI of the full E/I network does not change with a top-down modulation (Fig. 1, C; dashed colored lines), FI-E can nevertheless increase (Fig. 1, C; solid colored lines). We derive intuition for this key difference between FI and FI-E by considering the combined influence of input correlation and recurrent connectivity (captured by the ratio a in Fig. 1, C, middle plots. Light points show the ratio a before modulation; dark points, after modulation. Green and purple correspond to two different sets of network parameters. Fig. 1, Ci corresponds to input correlations = 0.9; Cii, to input correlations = 0.5).

Finally, we will further extend these ideas to a distributed population code by considering a framework with multiple E/I populations encoding a periodic stimulus variable [2]. In total, our results develop a new framework in which to understand how top-down modulation may exert a positive effect on cortical population codes.

References

1.
Kanashiro T, Ocker GK, Cohen MR, Doiron B. Attentional modulation of neuronal variability in circuit models of cortex. Elife 2017 Jun 7; 6:e23978.
2.
Getz M P, Huang C, Dunworth J, Cohen M R, Doiron B. Attentional modulation of neural covariability in a distributed circuit-based population model. Cosyne Abstracts 2018, Denver, CO, USA.

P71 Stimulus integration and categorization with bump attractor dynamics

Jose M. Esnaola-Acebes¹, Alex Roxin¹, Klaus Wimmer¹, Bharath C. Talluri², Tobias Donner^2,3

¹Centre de Recerca Matemàtica, Computational Neuroscience group, Barcelona, Spain; ²University Medical Center Hamburg-Eppendorf, Department of Neurophysiology & Pathophysiology, Hamburg, Germany; ³University of Amsterdam, Department of Psychology, Amsterdam, The Netherlands

Correspondence: Jose M. Esnaola-Acebes (jmesnaola@crm.cat)

BMC Neuroscience 2019, 20(Suppl 1):P71

Perceptual decision making often involves making categorical judgments based on estimations of continuous stimulus features. It has recently been shown that committing to a categorical choice biases a subsequent report of the stimulus estimate by selectively increasing the weighting of choice-consistent evidence [1]. This phenomenon, known as confirmation bias, commonly results in a suboptimal performance in people’s perceptual decisions. The underlying neural mechanisms that give rise to this phenomenon are still poorly understood.

Here we develop a computational network model that can integrate a continuous stimulus feature such as motion direction and can also account for a subsequent categorical choice. The model, a ring attractor network, represents the estimate of the integrated stimulus direction in the phase of an activity bump. A categorical choice can then be achieved by applying a decision signal at the end of the trial forcing the activity bump to move to one of two opposite positions. We reduced the network dynamics to a two-dimensional equation for the amplitude and the phase of the bump which allows for studying evidence integration analytically. The model can account for qualitatively distinct decision behaviors, depending on the relative strength of sensory stimuli compared to the amplitude of the bump attractor. When sensory inputs dominate over the intrinsic network dynamics, later parts of the stimulus have a higher impact on the final phase and the categorical choice than earlier parts (“recency” regime). On the other hand, when the internal dynamics are stronger, the temporal weighting of stimulus information is uniform. The corresponding psychophysical kernels are consistent with experimental observations [2]. We then simulated how stimulus estimation is affected by an intermittent categorical choice [1] by applying the decision signal after the first half of the stimulus. We found that this biases the resulting stimulus estimate at the end of the trial towards larger values for stimuli that are consistent with the categorical choice and towards smaller values for stimuli that are inconsistent, resembling the experimentally observed confirmation bias.

Our work suggests bump attractor dynamics as a potential underlying mechanism of stimulus integration and perceptual categorization.

Acknowledgments: Funded by the Spanish Ministry of Science, Innovation and Universities and the European Regional Development Fund (grants RYC-2015-17236, BFU2017-86026-R and MTM2015-71509-C2-1-R) and by the Generalitat de Catalunya (grant AGAUR 2017 SGR 1565).

References

1.
Talluri BC, Urai AE, Tsetsos K, Usher M, Donner TH. Confirmation bias through selective overweighting of choice-consistent evidence. Current Biology 2018 Oct 8;28(19):3128–35.
2.
Wyart V, De Gardelle V, Scholl J, Summerfield C. Rhythmic fluctuations in evidence accumulation during decision making in the human brain. Neuron 2012 Nov 21;76(4):847–58.

P72 Topological phase transitions in functional brain networks

Fernando Santos¹, Ernesto P Raposo², Maurício Domingues Coutinho-Filho², Mauro Copelli², Cornelis J Stam³, Linda Douw⁴

¹Universidade Federal de Pernambuco, Departamento de Matemática, Recife, Brazil; ²Universidade Federal de Pernambuco, Departamento de Física, Recife, Brazil; ³Vrije University Amsterdam Medical Center, Department of Clinical Neurophysiology and MEG Center, Amsterdam, Netherlands; ⁴Vrije University Amsterdam Medical Center, Department of Anatomy & Neurosciences, Amsterdam, Netherlands

Correspondence: Fernando Santos (fansantos@dmat.ufpe.br)

BMC Neuroscience 2019, 20(Suppl 1):P72

Functional brain networks are often constructed by quantifying correlations between time series of activity of brain regions. Their topological structure includes nodes, edges, triangles and even higher-dimensional objects. Topological data analysis (TDA) is the emerging framework to process datasets under this perspective. In parallel, topology has proven essential for understanding fundamental questions in physics. Here we report the discovery of topological phase transitions in functional brain networks by merging concepts from TDA, topology, geometry, physics, and network theory. We show that topological phase transitions occur when the Euler entropy has a singularity, which remarkably coincides with the emergence of multidimensional topological holes in the brain network, as illustrated in Fig. 1. The geometric nature of the transitions can be interpreted, under certain hypotheses, as an extension of percolation to high-dimensional objects. Due to the universal character of phase transitions and noise robustness of TDA, our findings open perspectives towards establishing reliable topological and geometrical markers for group and possibly individual differences in functional brain network organization.

P73 A whole-brain spiking neural network model linking basal ganglia, cerebellum, cortex and thalamus

Carlos Gutierrez¹, Jun Igarashi², Zhe Sun², Hiroshi Yamaura³, Tadashi Yamazaki⁴, Markus Diesmann⁵, Jean Lienard¹, Heidarinejad Morteza², Benoit Girard⁶, Gordon Arbuthnott⁷, Hans Ekkehard Plesser⁸, Kenji Doya¹

¹Okinawa Institute of Science and Technology, Neural Computation Unit, Okinawa, Japan; ²Riken, Computational Engineering Applications Unit, Saitama, Japan; ³The University of Electro-Communications, Tokyo, Japan; ⁴The University of Electro-Communications, Graduate School of Informatics and Engineering, Tokyo, Japan; ⁵Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6) & Institute for Advanced Simulation (IAS-6), Jülich, Germany; ⁶Sorbonne Universite, UPMC Univ Paris 06, CNRS, Institut des Systemes Intelligents et de Robotique (ISIR), Paris, France; ⁷Okinawa Institute of Science and Technology, Brain Mechanism for Behaviour Unit, Okinawa, Japan; ⁸Norwegian University of Life Sciences, Faculty of Science and Technology, Aas, Norway

Correspondence: Carlos Gutierrez (carlos.gutierrez@oist.jp)

BMC Neuroscience 2019, 20(Suppl 1):P73

The neural circuit linking the basal ganglia, the cerebellum and the cortex through the thalamus plays an essential role in motor and cognitive functions. However, how such functions are realized by multiple loop circuits with neurons of multiple types is still unknown. In order to investigate the dynamic nature of the whole-brain network, we built biologically constrained spiking neural network models of the basal ganglia [1, 2, 3], cerebellum, thalamus, and the cortex [4, 5] and ran an integrated simulation on K supercomputer [8] using NEST 2.16.0 [6, 7, 9].

We replicated resting state activities of 1 biological second of time in models with increasing scales, from 1x1mm² to 9x9mm² of cortical surface, the latter of which includes 35 million neurons and 66 billion synapses in total. Simulations using a hybrid parallelization approach showed a good weak scaling performance in simulation time lasting between 15–30 minutes, but identified a problem of long time (between 6–9 hours) required for network building.

We also evaluated the properties of action selection with realistic topographic connections in the basal ganglia circuit in 2-D target reaching task and observed selective activation and inhibition of neurons in preferred directions in every nucleus leading to the output. Moreover, we performed tests of reinforcement learning based on dopamine-dependent spike-timing dependent synaptic plasticity.

References

1.
Liénard J, Girard B. A biologically constrained model of the whole basal ganglia addressing the paradoxes of connections and selection. Journal of computational neuroscience 2014 Jun 1;36(3):445–68.
2.
Liénard J, Girard B, Doya K, et al. Action selection and reinforcement learning in a Basal Ganglia model. In Eighth International Symposium on Biology of Decision Making 2018 (Vol. 6226, pp. 597–606). Springer.
3.
Gutierrez CE, et al. Spiking neural network model of the basal ganglia with realistic topological organization. Advances in Neuroinformatics 2018, https://doi.org/10.14931/aini2018.ps.15 [Poster].
4.
Igarashi J, Moren K, Yoshimoto J, Doya K. Selective activation of columnar neural population by lateral inhibition in a realistic model of primary motor cortex. In Neuroscience 2014, the 44th Annual Meeting of the Society for Neuroscience (SfN 2014) Nov 15th. [Poster].
5.
Zhe S, Igarashi J. A Virtual Laser Scanning Photostimulation Experiment of the Primary Somatosensory Cortex. In The 28th Annual Conference of the Japanese Neural Network Society 2018 Oct (pp. 116). Okinawa Institute of Science and Technology.
6.
Gewaltig MO, Diesmann M. Nest (neural simulation tool). Scholarpedia 2007 Apr 5;2(4):1430.
7.
Linssen C, et al. NEST 2.16.0. Zenodo 2018. https://doi.org/10.5281/zenodo.1400175.
8.
Miyazaki H, Kusano Y, Shinjou N, et al. Overview of the K computer system. Fujitsu Sci. Tech. J. 2012 Jul 1;48(3):302–9.
9.
Jordan J, Ippen T, Helias M, et al. Extremely scalable spiking neuronal network simulation code: from laptops to exascale computers. Frontiers in neuroinformatics 2018 Feb 16;12:2.

P74 Graph theory-based representation of hippocampal dCA1 learning network dynamics

Giuseppe Pietro Gava¹, Simon R Schultz², David Dupret³

¹Imperial College London, Biomedical Engineering, London, United Kingdom; ²Imperial College London, London, United Kingdom; ³University of Oxford, Medical Research Council Brain Network Dynamics Unit, Department of Pharmacology, Oxford, United Kingdom

Correspondence: Giuseppe Pietro Gava (giuseppepietrogava@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P74

Since the discovery of place and grid cells, the hippocampus has been attributed a particular sensitivity to the spatial-contextual features of memory and learning. A crucial area in these processes is the dorsal CA1 hippocampus region (dCA1), where both pyramidal cells and interneurons are found. The former are excitatory cells that display tuning to spatial location (place fields), whilst the latter regulate the network with inhibitory inputs. Graph theory gives us powerful tools for studying such complex systems by representing, analyzing and modelling the dynamics of hundreds of components (neurons) interacting together. Graph theory-based methods are employed by network neuroscience to yield insightful descriptions of neural networks dynamics [1].

Here, we propose a graph theory-based analysis of the dCA1 network, recorded from mice engaged in a condition place preference task. In this protocol the animals first explore a familiar environment (fam). Afterwards, it is introduced to two novel arenas (pre/post), which are later individually associated with different reward dispensers. We analyse electro-physiological data from 2 animals, 7 recording days combined, for a total of 617 putative pyramidal cells and 38 putative interneurons. To investigate the dynamics of the recorded network, we apply directed weighted graphs using a directional biophysically-inspired measure of the functional connectivity between each neuron.

As of now, we have limited our analysis to the dynamics of putative pyramidal cells in the network. As the task progresses and the animal learns the reward associations, we observe an overall increase in the average strength (S) of the network (S_pre = 0.41±0.08 / S_post = 0.78±0.09, mean ± s.e.m. normalized units). The average firing rate (FR), instead, peaks only during the first exploration of the novel environment and decreases thereafter—(FR_fam = 0.78±0.02 / FR_pre = 0.95±0.02 / FR_post = 0.82±0.02). Together with S, an overall decrease in the shortest path length (PL) in the network suggests that the system shifts towards a more small-world structure (PL_fam = 1±0 / PL_pre = 0.76±0.09 / PL_post = 0.61±0.10). This topology has been described to be more adaptive and efficient, thus fit to encode new information [2]. The evolution of the network during learning is also indicated by its Riemannian distance from the activity patterns evoked in fam. This measure increases from the exposition to pre (0.88±0.02) to the end of learning (0.98±0.01), decreases in post (0.91±0.02) and is at its minimum when fam is recalled (0.78±0.06). These results suggest that the evoked patterns in pre and post are similar, as they represent the same environment, even if they display different network activity measures (S, FR, PL). We hypothesize that these metrics might indicate the learning-related dynamics that favor the encoding of new information.

We are to integrate these findings with information measures at the individual neuron level. The finer structure of the network may be investigated: from changes in pyramidal cells’ spatial tuning, to diverse regulatory action of the interneuron population. Together, these analyses will provide us with an insightful picture of the dCA1 network dynamics during learning.

References

1.
Bassett DS, Sporns O. Network neuroscience. Nature neuroscience 2017 Mar;20(3):353.
2.
Bassett DS, Bullmore ED. Small-world brain networks. The neuroscientist 2006 Dec;12(6):512–23.

P75 Measurement-oriented deep-learning workflow for improved segmentation of myelin and axons in high-resolution images of human cerebral white matter

Predrag Janjic¹, Kristijan Petrovski¹, Blagoja Dolgoski², John Smiley³, Panče Zdravkovski², Goran Pavlovski⁴, Zlatko Jakjovski⁴, Natasa Davceva⁴, Verica Poposka⁴, Aleksandar Stankov⁴, Gorazd Rosoklija⁵, Gordana Petrushevska², Ljupco Kocarev⁶, Andrew Dwork⁵

¹Macedonian Academy of Sciences and Arts, Research Centre for Computer Science and Information Technologies, Skopje, Macedonia; ²School of Medicine, Ss. Cyril and Methodius University Skopje, Institute of Pathology, Skopje, Macedonia; ³Nathan S. Kline Institute for Psychiatric Research, New York, United States of America; ⁴School of Medicine, Ss. Cyril and Methodius University, Institute of Forensic Medicine, Skopje, Macedonia; ⁵New York State Psychiatric Institute, Columbia University, Division of Molecular Imaging and Neuropathology, New York, United States of America; ⁶Macedonian Academy of Sciences and Arts, Skopje, Macedonia

Correspondence: Predrag Janjic (predrag.a.janjic@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P75

Background: In CNS, the relationship between axon diameter and myelin thickness is more complex than in peripheral nerve. Standard segmentation of high-contrast electron micrographs (EM) segments the myelin accurately, but even in studies of regular, parallel fibers, this does not translate easily into measurements of individual axons and their myelin sheaths, Quantitative morphology of myelinated axons requires measuring the diameters of thousands of axons and the thickness of each axon’s myelin sheath. We describe here a procedure for automated refinement of segmentation and measurement of each myelinated axon and its sheath in EMs (11 nm/pixel) of arbitrarily oriented prefrontal white matter (WM) from human autopsies (Fig. 1A).

New methods: Preliminary segmentation of myelin, axons and background in the original images, using ML techniques based on manually selected filters (Fig. 1B), are postprocessed for correcting of typical, systematic errors in the preliminary-segmentation. Final, refined and corrected segmentation is achieved by deep neural networks (DNN) which classify the central pixel of an input fragment (Fig. 1D). We use two DNN architectures: (i) Denoising auto-encoder using convolutional neural network (CNN) layers for initialization of weights to the first receptive layer of the main DNN, which is built in (ii) classical multilayer CNN architecture Automated routine gives radial measurements of each putative axon and its myelin sheath, after it rejects measures encountering predefined artifacts and excludes fibers that fail to satisfy certain predefined conditions. The ML processing, after a working dataset of 30 images, 2048x2048 pixel is preprocessed, takes ~ 1h 40min. for complete pixel-based segmentation of ~ 8,000 ÷ 9,000 fiber ROIs per set, on a commercial PC equipped with a single GTX-1080 class GPU.

Results: This routine improved segmentation of three sets of 30 annotated images (sets 1 and 2 from prefrontal white matter, while set 3 was from optic nerve), with DNN trained only with a subset of set 1 images. Total number of myelinated axons identified by the DNN differed from the human segmentation by 0.2%, 2.9%, and − 5.1% for sets 1–3, respectively. G-ratios differed by 2.96%, 0.74% and 2.83%. Myelin thickness measurements were even closer, Fig. 1E. Intraclass correlation coefficients between DNN and annotated segmentation, were mostly>0.9, indicating nearly interchangeable performance.

Comparison with existing method(s): Measurement-oriented studies of arbitrarily oriented fibers (appearing in single images) from human frontal white matter are rare. Published studies of spinal cord white matter or peripheral nerve typically measure aggregated area of myelin sheaths, allowing only an aggregate estimation of average g-ratio, assuming counterfactually that g-ratio is the same for all fibers. Thus, our method fulfills an important need.

Conclusions: Automated segmentation and measurement of axons and myelin is more complex than it appears initially. We have developed a feasible approach that has proven comparable to human segmentation in our tests so far, and the trained networks generalize very well on datasets other than those used in training.

Acknowledgements: This work has been funded by National Institutes of Health, NIMH under MH98786.

P76 Spike latency reduction generates efficient encoding of predictions

Pau Vilimelis Aceituno¹, Juergen Jost², Masud Ehsani¹

¹Max Planck Institute for Mathematics in the Sciences, Cognitive group of Juergen Jost, Leipzig, Germany; ²Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany

Correspondence: Pau Vilimelis Aceituno (pau.aceituno@mis.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):P76

Living organisms make predictions in order to survive, posing the question of how do brains learn to make those predictions. General models based on classical conditioning [1] assume that prediction performance is feed back into the predicting neural population. However, recent studies have found that sensory neurons without feedback from higher brain areas encode predictive information [4]. Therefore, a bottom-up process without explicit feedback should also generate predictions. Here we present such a mechanism through latency reduction, an effect of Synaptic Time-Dependent Plasticity (STDP) [3].

We study leaky-integrate and fire neurons with a refractory period (LIF), each one getting a fixed input spike train that is repeated many times. The weights of the synapses change following the Synaptic Time-Dependent Plasticity (STDP) with soft bounds. From this we use a variety of mathematical tools and simulations to create the following argument:

Short Temporal Effects: We analyze how do postsynaptic spikes evolve, showing that a single postsynaptic spike reduces its latency
Long Temporal Effects: We prove that the postsynaptic spike train becomes very dense at input onset and that the number of postsynaptic spikes reduces with the stimulus repetition.
Coding: The concentration of inputs makes the code more efficient in metabolic and decoding terms.
Predictions: STDP makes postsynaptic neurons fire at the onset of the input spike train, which might be before the stimulus if the input spike train includes a pre-stimulus clue, thus generating predictions.

We show here (Fig. 1) that STDP in combination with regularly timed presynaptic spikes generates postsynaptic codes that are efficient and explain how forecasting are phenomena that emerge in an unsupervised way with a simple mechanistic interpretation. We believe that this idea offers an interesting complement to classical supervised predictive coding schemes in which prediction errors are feed back into the coding neurons. Furthermore, the concentration of postsynaptic spikes at stimulus onset can be interpreted in information theoretical terms as a way to improve the code in terms of error-resilience. Finally, we speculate that the fact that the same mechanism can be used to generate predictions as well as improve the effectiveness and metabolic efficiency of the neural code might give insights into how the ability of the nervous system to forecast might have evolved.

References

1.
Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. MIT Press 2001.
2.
Song S, Miller KD, Abbott LF. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nature neuroscience 2000 Sep;3(9):919.
3.
Guyonneau R, VanRullen R, Thorpe SJ. Neurons tune to the earliest spikes through STDP. Neural Computation 2005 Apr 1;17(4):859–79.
4.
Palmer SE, Marre O, Berry MJ, Bialek W. Predictive information in a sensory population. Proceedings of the National Academy of Sciences 2015 Jun 2;112(22):6908–13.

P77 Differential diffusion in a normal and a multiple sclerosis lesioned connectome with building blocks of the peripheral and central nervous system

Oliver Schmitt¹, Christian Nitzsche¹, Frauke Ruß¹, Lena Kuch¹, Peter Eipert¹

¹University of Rostock, Department of Anatomy, Rostock, Germany

Correspondence: Oliver Schmitt (schmitt@med.uni-rostock.de)

BMC Neuroscience 2019, 20(Suppl 1):P77

The structural connectome (SC) of the rat nervous system has been built by collating neuronal connectivity information from tract tracing publications [1]. In most publications semi quantitative estimates of axonal densities are indicated. These connectivity weights and the orientation of connections (source-target of action potentials) were imported into neuroVIISAS [2].

The connectivity of the peripheral nervous system and of the spinal cord allows a continuous reconstruction of the transfer of afferent signals from the periphery, respectively, dorsal root ganglions via intraspinal or medullary secondary neurons. As opposed to this the efferent pathway from the central peripheral nervous system (PNS) through primary vegetative neurons as well as α-motoneurons is available, too. This thorough connectome data allows the investigation of complete peripheral-central-afferents pathways as well as central-peripheral-efferent pathways by dynamic analyses.

The propagation of signals derived from basic diffusion processes [3], the Gierer-Meinhardt [4] and Mimura-Murray [5] diffusion models (DM) was investigated. The models have been adapted to a weighted and directed connectome. The application of DM in SCs exhibit a lower complexity by contrast with coupled single neuron models (FitzHugh Nagumo (FHN)) [3] or models of spiking LIF populations. To compare outcomes of DM the FHN model has been realized in the same SC (Fig. 1).

Modeling of diseases like Alzheimer and Parkinson as well as multiple sclerosis (MS) in SC helps to understand spreading of pathology and predicting changes of white and gray matter [6-8]. The reduction of connection weights by modelling reflect the effect of myelin degeneration in MS. The change [9] of diffusibility of a lesioned afferent-efferent loop in the rat PNS-ZNS has been analyzed. A reduction of diffusion was observed in the GM and MM models following linear and nonlinear reduction of connectivity weights of central processes of the dorsal root ganglion neurons, cuneate and gracile nuclei. The change of diffusibility shows slight effects in the motoric pathway.

The effects of the two models coincides with clinical observations with regard to paresthesias and spaticity because changes of diffusion were most prominent in the somatosensory and somatomotoric system. Further investigations will be performed to analyze functional effects of local white matter lesions as well as long term functional changes.

References

1.
Schmitt O, Eipert P, Kettlitz R, Leßmann F, Wree A. The connectome of the basal ganglia. Brain Structure and Function 2016 Mar 1;221(2):753–814.
2.
Schmitt O, Eipert P. neuroVIISAS: approaching multiscale simulation of the rat connectome. Neuroinformatics 2012 Jul 1;10(3):243–67.
3.
Messé A, Hütt MT, König P, Hilgetag CC. A closer look at the apparent correlation of structural and functional connectivity in excitable neural networks. Scientific reports 2015 Jan 19;5:7870.
4.
Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik 1972 Dec 1;12(1):30–9.
5.
Nakao H, Mikhailov AS. Turing patterns in network-organized activator–inhibitor systems. Nature Physics 2010 Jul;6(7):544.
6.
Ji GJ, Ren C, Li Y, Sun J, et al. Regional and network properties of white matter function in Parkinson’s disease. Human brain mapping 2019 Mar;40(4):1253–63.
7.
Ye C, Mori S, Chan P, Ma T. Connectome-wide network analysis of white matter connectivity in Alzheimer’s disease. NeuroImage: Clinical 2019 Jan 1;22:101690.
8.
Mangeat G, Badji A, Ouellette R, et al. Changes in structural network are associated with cortical demyelination in early multiple sclerosis. Human brain mapping 2018 May;39(5):2133–46.
9.
Schwanke S, Jenssen J, Eipert P, Schmitt O. Towards Differential Connectomics with NeuroVIISAS. Neuroinformatics 2019 Jan 1;17(1):163–79.

P78 Linking noise correlations to spatiotemporal population dynamics and network structure

Yanliang Shi¹, Nicholas Steinmetz², Tirin Moore³, Kwabena Boahen⁴, Tatiana Engel¹

¹Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, United States of America; ²University of Washington, Department of Biological Structure, Seattle, United States of America; ³Stanford University, Department of Neurobiology, Stanford, California, United States of America; ⁴Stanford University, Departments of Bioengineering and Electrical Engineering, Stanford, United States of America

Correspondence: Yanliang Shi (shi@cshl.edu)

BMC Neuroscience 2019, 20(Suppl 1):P78

Neocortical activity fluctuates endogenously, with much variability shared among neurons. These co-fluctuations are generally characterized as correlations between pairs of neurons, termed noise correlations. Noise correlations depend on anatomical dimensions, such as cortical layer and lateral distance, and they are also dynamically influenced by behavioral states, in particular, during spatial attention. Specifically, recordings from laterally separated neurons in superficial layers find a robust reduction of noise correlations during attention [1]. On the other hand, recordings from neurons in different layers of the same column find that changes of noise correlations differ across layers and overall are small compared to lateral noise-correlation changes [2]. Evidently, these varying patterns of noise correlations echo the wide-scale population activity, but the dynamics of population-wide fluctuations and their relationship to the underlying circuitry remain unknown.

Here we present a theory which relates noise correlations to spatiotemporal dynamics of population activity and the network structure. The theory integrates vast data on noise correlations with our recent discovery that population activity in single columns spontaneously transitions between synchronous phases of vigorous (On) and faint (Off) spiking [3]. We develop a network model of cortical columns, which replicates cortical On-Off dynamics. Each unit in the network represents one layer—superficial or deep—of a single column (Fig. 1a). Units are connected laterally to their neighbors within the same layer, which correlates On-Off dynamics across columns. Visual stimuli and attention are modeled as external inputs to local groups of units. We study the model by simulations and also derive analytical expressions for distance-dependent noise correlations. To test the theory, we analyze linear microelectrode array recordings of spiking activity from all layers of the primate area V4 during an attention task.

First, at the scale of single columns, the theory accurately predicts the broad distribution of attention-related changes of noise-correlations in our laminar recordings, indicating that they largely arise from the On-Off dynamics. Second, the network model mechanistically explains differences in attention-related changes of noise-correlations at different lateral distances. Due to spatial connectivity, noise correlations decay exponentially with lateral distance, characterized by the decay-constant called correlation length (Fig. 1b) . Correlation length depends on the strength of lateral connections, but it is also modulated by attentional inputs, which effectively regulate the relative influence of lateral inputs. Thus changes of lateral noise-correlations mainly arise from changes in the correlation length. The model predicts that at intermediate lateral distances (<1mm), noise-correlation changes decrease or increase with distance, when the correlation-length increases or decreases, respectively. To test these predictions, we used distances between receptive-field centers to estimate lateral shifts in our laminar recordings (Fig. 1c). We found that during attention, correlation length decreases in superficial and increases in deep layers, indicating differential modulation of superficial and deep layers. (Fig. 1d). Our work provides a unifying framework that links network mechanisms shaping noise correlations to dynamics of population activity and underlying cortical circuit structure.

References

1.
Cohen MR, Maunsell JH. Attention improves performance primarily by reducing interneuronal correlations. Nature neuroscience 2009 Dec;12(12):1594.
2.
Nandy AS, Nassi JJ, Reynolds JH. Laminar organization of attentional modulation in macaque visual area V4. Neuron 2017 Jan 4;93(1):235–46.
3.
Engel TA, Steinmetz NA, Gieselmann MA, Thiele A, Moore T, Boahen K. Selective modulation of cortical state during spatial attention. Science 2016 Dec 2;3.

P79 Modeling the link between optimal characteristics of saccades and cerebellar plasticity

Hari Kalidindi¹, Lorenzo Vannucci¹, Cecilia Laschi¹, Egidio Falotico¹

¹Scuola Superiore Sant’Anna Pisa, The BioRobotics Institute, Pontedera, Italy

Correspondence: Hari Kalidindi (h.kalidindi@santannapisa.it)

BMC Neuroscience 2019, 20(Suppl 1):P79

Plasticity in cerebellar synapses is important for adaptability and fine tuning of fast reaching movements. The perceived sensory errors between the desired and actual movement outcomes are commonly considered to induce plasticity in the cerebellar synapses, with an objective to improve the desirability of the executed movements. In fast goal-directed eye movements called saccades, the desired outcome is to reach a given target location in minimum-time, with accuracy. However, an explicit encoding of this desired outcome is not observed in the cerebellar inputs prior to the movement initiation. It is unclear how the cerebellum is able to process only partial error information, that is the final reaching error signal obtained from sensors, to control both the reaching time as well as the precision of fast movements in an adaptive manner. We model the bidirectional plasticity at the parallel fiber to Purkinje cell synapses that can account for the mentioned saccade characteristics. We provide a mathematical and robot experimental demonstration of how the equations governing the cerebellar plasticity are determined by the desirability of the behavior. In the experimental results, the model output activity displays a definite encoding of eye speed and displacement during the movement. This is in line with the corresponding neurophysiological recordings of Purkinje cell populations in the cerebellar vermis of rhesus monkeys. The proposed modeling strategy, due to its mechanistic form, is suitable for studying the link between motor learning rules observed in biological systems and their respective behavioral principles.

P80 Attractors and flows in the neural dynamics of movement control

Paolo Del Giudice¹, Gabriel Baglietto², Stefano Ferraina³

¹Istituto Superiore di Sanità, Rome, Italy; ²IFLYSIB Instituto de Fisica de Liquidos y Sistemas Biologicos (UNLP-CONICET), La Plata, Argentina; ³Sapienza University, Dept Physiology and Pharmacology, Rome, Italy

Correspondence: Paolo Del Giudice (paolo.delgiudice@iss.it)

BMC Neuroscience 2019, 20(Suppl 1):P80

Density-based clustering (DBC) [1] provides efficient representations of a multidimensional time series, allowing to cast it in the form of the symbolic sequence of the labels identifying the cluster to which each vector of instantaneous values belong. Such representation naturally lends itself to obtain compact descriptions of data from multichannel electrophysiological recordings.

We used DBC to analyze the spatio-temporal dynamics of dorsal premotor cortex in neuronal data recorded from two monkeys during a ‘countermanding’ reaching task: the animal must perform a reaching movement to a target on a screen (‘no-stop trials’), unless an intervening stop signal prescribes to withhold the movement (‘stop-trials’); no-stop (~70%) and stop trials (~30%) were randomly intermixed, and the stop signal occurred at variable times within the reaction time.

Multi-unit activity (MUA) was extracted from signals recorded using a 96-electrodes array. Performing DBC on the 96-dimensional MUA time series, we derived the corresponding discrete sequence of clusters’ centroid.

Through the joint analysis of such cluster sequences for no-stop and stop trials we show that reproducible cluster sequences are associated with the completion of the motor plan in no-stop trials, and that in stop trials the performance depends on the relative timing of such states and the arrival of the Stop signal.

Besides, we show that a simple classifier can reliably predict the outcome of stop trials from the cluster sequence preceding the appearance of the stop signal, at the single-trial level.

We also observe that, consistently with previous studies, the inter-trial variability of MUA configurations typically collapses around the movement time, and has minima corresponding to other behavioral events (Go signal; Reward); comparing the time profile of MUA inter-trial variability with the cluster sequences, we are led to ask whether the neural dynamics underlying the clusters sequence can be interpreted as attractor hopping. For this purpose we analyze the flow in the MUA configuration space: for each trial, and each time, the measured MUA values identify a point in the 96-dimensional space, such that each trial corresponds to a trajectory in this space, and a set of repeated trials to a bundle of trajectories, of which we can compute individual or average properties. We measure quantities suited to discriminate between a dynamics of convergence of the trajectories to a point attractor, from different flows in the MUA configuration space. We tentatively conclude that convergent attractor relaxation dynamics (in attentive wait conditions, as before the Go or the Reward events) coexist with coherent flows (associated with movement onset), in which low inter-trial variability of MUA configurations corresponds to a collapse in the directions of velocities (with high magnitude of the latter), like the system entering a funnel.

The ‘delay task’ (Go signal comes with a variable delay after the visual target), allows to further check our interpretation of specific MUA configurations (clusters) as being associated with the completion of the motor plan. Preliminary analysis shows that pre-movement-related MUA cluster sequences during delay trials are consistent with those from other trial types, though their time course qualitatively differs in the two monkeys, possibly reflecting different computational options.

Reference

1.
Baglietto G, Gigante G, Del Giudice P. Density-based clustering: A ‘landscape view’ of multi-channel neural data for inference and dynamic complexity analysis. PloS one 2017 Apr 3;12(4):e0174918.

P81 Information transmission in delay-coupled neuronal circuits

Jaime Sánchez Claros¹, Claudio Mirasso¹, Minseok Kang², Aref Pariz¹, Ingo Fischer¹

¹Institute for Cross-Disciplinary Physics and Complex Systems, Palma de Mallorca, Spain; ²Institute for Cross-Disciplinary Physics and Complex Systems, Osnabrck University, Osnabrck, Germany

Correspondence: Jaime Sánchez Claros (js.claros27@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P81

The information that we receive through our sensory system (e.g. sound, vision, pain, etc), needs to be transmitted to different regions of the brain for its processing. When these regions are sufficiently separated from each other, the latency in the communication can affect the synchronization state; it is possible that the regions synchronize in phase or out of phase, or even not synchronize [1]. These types of synchronization, when occur, can have important consequences in information transmission and processing [2].

Here we study the information transmission in a V and a circular motif (see Fig. 1). We initially use the Kuramoto model to describe the nodes dynamics and derive analytical stability solutions for the V-motif for different delays and coupling strengths among the neurons as well as different spiking frequencies. We then analyze the effect that a third connection would have on the stable solutions as we change its axonal delay and synaptic strength. For a more realistic model, we simulate the Hodgkin-Huxley neuron model. For the V-motif we find that the delay can play an important role in the efficiency of the signal transmission. When we introduce a direct connection between 1 and 3, we find changes in the stability conditions and so the efficacy of the information transmission. To distinguish between rate and temporal coding, we modulate one of the elements with low and high frequency signals, respectively, and investigate the signal transmission to the other neurons using delayed mutual information and delayed transfer entropy [3].

References

1.
Sadeghi S, Valizadeh A. Synchronization of delayed coupled neurons in presence of inhomogeneity. Journal of Computational Neuroscience 2014, 36, 55–66.
2.
Mirasso CR, Carelli PV, Pereira T, Matias FS, Copelli M. Anticipated and zero-lag synchronization in motifs of delay-coupled systems. Chaos 2017, 27,114305.
3.
Kirst C, Timme M, Battaglia D. Dynamic information routing in complex networks. Nature communication 2016, 7.

P82 A Liquid State Machine pruning method for identifying task specific circuits

Dorian Florescu

Coventry University, Coventry, United Kingdom

Correspondence: Dorian Florescu (dorian.florescu@coventry.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P82

The current lack of knowledge on the precise neural circuits responsible for performing sensory and motor tasks, despite the large amounts of neuroscience data available, significantly slows down the development of new treatments for impairments caused by neurodegenerative diseases.

The Liquid State Machine (LSM) is one of the widely used paradigms for modelling brain computation. This model consists of a fixed recurrent spiking neural network, called Liquid, and a linear Readout unit with adjustable synapses. The model possesses, under idealised conditions, universal real-time computing power [1]. It was shown that, when the connections in the Liquid are modelled as dynamical synapses, this model can reproduce accurately the behaviour of the rat cortical microcircuits [1]. However, it is still largely unknown which neurons and synapses in the Liquid play a key role in a task performed by the LSM. Several proposed methods train the Liquid in addition to the Readout [2], which leads to improvements in accuracy and network sparsity, but offers little insight into the functioning of the original Liquid.

In the typical LSM architecture, the spike trains generated by the Liquid neurons are filtered before being processed by the Readout. It was shown that using the exact spike times generated by the Liquid neurons, rather than the filtered spike times, results in a much better performance of LSMs on training tasks. The algorithm introduced, called the Orthogonal Forward Regression with Spike Times (OFRST), leads to higher accuracy and fewer Readout connections than the state-of-the-art algorithm [3].

This work proposes an analysis of the underlying mechanisms used by the LSM to perform a computational task by searching for the key neural circuits involved. Given an LSM trained on a classification task, a new algorithm is introduced that identifies the corresponding task specific circuit (TSC), defined as the set of neurons and synapses in the Liquid that have a contribution to the Readout output. Thorough numerical simulations, I show that the TSC computed with the proposed algorithm has fewer neurons and higher performance when the training is done with OFRST compared with other state-of-the-art training methods (Fig. 1).

I introduce a new representation for the Liquid dynamical synapses, which demonstrates that they can be mapped onto operators on the Hilbert space of spike trains. Based on this representation, I develop a novel algorithm that removes iteratively the synapses of a TSC based on the exact spike times generated by the Liquid neurons. Additional numerical simulations show that the proposed algorithm improves the LSM classification performance and leads to a significantly sparser representation. For the same initial Liquid, but different tasks, the proposed algorithm results in different TSCs that, in some cases, have no neurons in common. These results can lead to new methods to synthesize Liquids by interconnecting dedicated neural circuits.

References

1.
Maass W, Natschläger T, Markram H. Computational models for generic cortical microcircuits. Computational neuroscience: A comprehensive approach 2004;18:575–605.
2.
Yin J, Meng Y, Jin Y. A developmental approach to structural self-organization in reservoir computing. IEEE transactions on autonomous mental development 2012 Dec;4(4):273–89.
3.
Florescu D, Coca D. Learning with precise spike times: A new approach to select task-specific neurons. In Computational and Systems Neuroscience (COSYNE) 2018 Mar 2. COSYNE.

P83 Cross-frequency coupling along the soma-apical dendritic axis of model pyramidal neurons

Melvin Felton¹, Alfred Yu², David Boothe², Kelvin Oie², Piotr Franaszczuk²

¹U.S. Army Research Laboratory, Computational and Information Sciences Division, Adelphi, MD, United States of America; ²U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: Piotr Franaszczuk (pfranasz@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P83

Cross-frequency coupling (CFC) has been associated with mental processes like perceptual and memory-related tasks, and is often observed via EEG and LFP measurements [1]. There are a variety of physiological mechanisms believed to produce CFC, and different types of network properties can yield distinct CFC signatures [2]. While it is widely believed that pyramidal neurons play an important role in the occurrence of CFC, the detailed nature of the contribution of individual pyramidal neurons to CFC detected via large-scale measures of brain activity is still uncertain.

As an extension of our single model neuron resonance analysis [3], we examined CFC along the soma-apical dendrite axis of realistic models of pyramidal neurons. We configured three models to capture some variety that exists among pyramidal neurons in the neocortical and limbic regions of the brain. Our baseline model had the least amount of regional variation in conductance densities of the Ih and high- and low-threshold Ca2+ conductances. The second model had an exponential gradient in Ih conductance density along the soma-apical dendrite axis, typical of some neocortical and hippocampal pyramidal neurons. The third model contained both the exponential gradient in Ih conductance density and a distal apical “hot zone” where the high- and low-threshold Ca2+conductances had densities 10 and 100 times higher, respectively, than anywhere else in the model (cf., [3]). We simulated two current injection scenarios: 1) perisomatic 4 Hz modulation with perisomatic, mid-apical, and distal apical 40 Hz injections; and 2) distal 4 Hz modulation with perisomatic, mid-apical, and distal 40 Hz injections. We used two metrics to quantify the strength of CFC—height ratio and modulation index [4].

We found that CFC strength can be predicted from the passive filtering properties of the model neuron. Generally, regions of the model with much larger membrane potential fluctuations at 4 Hz than at 40 Hz (high Vm4Hz/Vm40Hz) had stronger CFC. The strongest CFC values were observed in the baseline model, but when the exponential gradient in Ih conductance density was added, CFC strength decreased by almost 50% at times. On the other hand, including the distal hot zone increased CFC strength slightly above the case with only the exponential gradient in Ih conductance density.

This study can potentially shed light on which configurations of fast and slow input to pyramidal neurons can produce the strongest CFC, and where exactly within the neuron CFC is strongest. In addition, this study can illuminate the reasons why there may be differences between CFC strength observed in different regions of the brain and between different populations of neurons.

References

1.
Tort AB, Komorowski RW, Manns JR, Kopell NJ, Eichenbaum H. Theta–gamma coupling increases during the learning of item–context associations. Proceedings of the National Academy of Sciences 2009 Dec 8;106(49):20942–7.
2.
Hyafil A, Giraud AL, Fontolan L, Gutkin B. Neural cross-frequency coupling: connecting architectures, mechanisms, and functions. Trends in neurosciences 2015 Nov 1;38(11):725–40.
3.
Felton Jr MA, Alfred BY, Boothe DL, Oie KS, Franaszczuk PJ. Resonance Analysis as a Tool for Characterizing Functional Division of Layer 5 Pyramidal Neurons. Frontiers in Computational Neuroscience 2018;12.
4.
Tort AB, Komorowski R, Eichenbaum H, Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of neurophysiology 2010 May 12;104(2):1195–210.

P84 Regional connectivity increases low frequency power and heterogeneity

David Boothe, Alfred Yu, Kelvin Oie, Piotr Franaszczuk

U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: David Boothe (david.l.boothe7.civ@mail.mil)

BMC Neuroscience 2019, 20(Suppl 1):P84

The relationship between neuronal connectivity and frequency in the power spectrum of calculated local field potentials is poorly characterized in models of cerebral cortex. Here we present a simulation of cerebral cortex based on the Traub model [1] implemented in the GENESIS neuronal simulation environment. We found that this model tended to produce high neuronal firing rates and strongly rhythmic activity in response to increases in neuronal connectivity. In order to simulate spontaneous brain activity with a 1/f power spectrum as observed using electroencephalogram (EEG) (cf. [2]), and to faithfully recreate the sparse nature of cortical neuronal activity we re-tuned the original Traub parameters to eliminate intrinsic neuronal activity and removed the gap junctions. While gap junctions are known to exist in adult human cortex, their exact functional role in generating spontaneous brain activity is at present poorly characterized. Tuning out intrinsic neuronal activity allows changes to the synaptic connectivity to be central to changing overall model activity.

The model we present here consists of 16 simulated cortical regions each containing 976 neurons (15,616 neurons total). Simulated cortical regions are connected via short association fibers between adjacent cortical regions originating from pyramidal cells in cortical layer 2/3 (P23s). In the biological brain these short association fibers connect local cortical regions that tend to share a function like the myriad of visual areas of the posterior, parietal and temporal cortices [4]. Because of their ubiquity across cortex short association fibers were a natural starting point for our simulations. Long range layer 2/3 pyramidal cell connections terminated on neurons in other cortical regions with the same connectivity probabilities that they have locally within a region. We then varied the relative levels of long range and short-range connectivity and observed the impact on overall model activity. Because model dynamics were very sensitive to the overall number of connections we had to be careful that the simulations we were comparing only varied in proportion of long and short range connections and not in terms of total connectivity.

Our starting point for these simulations was a model with relatively sparse connectivity, which exhibited 1/f power spectrum with strong peaks in power spectral density at 20 Hz and 40 Hz ((Fig. 1), black line). We found that increases in long range connectivity increased power across the entire 1 to 100 Hz range of the overall local field potential of the model ((Fig. 1), blue line) and also increased heterogeneity in the power spectra of the 16 individual cortical regions. Increasing short range connectivity had the opposite effect, with overall power in the low frequency range (1 to 10 Hz) being reduced while the relative intensity at 20 Hz and 40 Hz remained constant (Fig. 1, red line). We will explore how consistent this effect is across varying levels of short- and long-range connectivity and model configuration.

References

1.
Traub RD, Contreras D, Cunningham MO, et al. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. Journal of neurophysiology 2005 Apr;93(4):2194–232.
2.
Le Van Quyen M. Disentangling the dynamic core: a research program for a neurodynamics at the large-scale. Biological research 2003;36(1):67–88.
3.
Salin PA, Bullier J. Corticocortical connections in the visual system: structure and function. Physiological reviews 1995 Jan 1;75(1):107–54.

P85 Cortical folding modulates the effect of external electrical fields on neuronal function

Alfred Yu, David Boothe, Kelvin Oie, Piotr Franaszczuk

U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: David Boothe (david.l.boothe7.civ@mail.mil)

BMC Neuroscience 2019, 20(Suppl 1):P85

Transcranial electrical stimulation produces an electrical field that propagates through cortical tissue. Finite element modeling has shown that individual variation in spatial morphology can lead to variability in field strength within target structures across individuals [1]. Using GENESIS, we simulated a 10x10 mm network of neurons with spatial arrangements simulating microcolumns of a single cortical region spread across sulci and gyri. We modeled a transient electrical field with distance-dependent effects on membrane polarization, simulating the nonstationary effects of electrical fields on neuronal activity at the compartment level. In previous work, we have modeled applied electrical fields using distant electrodes, resulting in uniform orientation and field strength across all compartments. In this work, we examine a more realistic situation with distance- and orientation-dependent drop-off in field strength. As expected, this change resulted in a greater degree of functional variability between microcolumns and reduced overall network synchrony. We show that the spatial arrangement of cells within sulci and gyri yields sub-populations that are differentially susceptible to externally applied electric fields, in both their firing rates and the functional connectivity with adjacent microcolumns. In particular, pyramidal cell populations with inconsistently oriented apical dendrites produce less synchronized activity within an applied external field. Further, we find differences across cell types, such that cells with reduced dendritic arborization had greater sensitivity to orientation changes due to placement within sulci and gyri. Given that there is individual variability in the spatial arrangement of even primary cortices [2], our findings indicate that individual differences in outcomes of neurostimulation can be the result of variations in local topography. In summary, aside from increasing cortical surface area and altering axonal connection distances, cortical folding may additionally shape the effects of spatially local influences such as electrical fields.

References

1.
Datta A. Inter-individual variation during transcranial direct current stimulation and normalization of dose using MRI-derived computational models. Frontiers in psychiatry 2012 Oct 22;3:91.
2.
Rademacher J, Caviness Jr VS, Steinmetz H, Galaburda AM. Topographical variation of the human primary cortices: implications for neuroimaging, brain mapping, and neurobiology. Cerebral Cortex 1993 Jul 1;3(4):313–29.

P86 Data-driven modeling of mouse CA1 and DG neurons

Paola Vitale¹, Carmen Alina Lupascu¹, Luca Leonardo Bologna¹, Mala Shah², Armando Romani³, Jean-Denis Courcol³, Stefano Antonel³, Werner Alfons Hilda Van Geit³, Ying Shi³, Julian Martin Leslie Budd⁴, Attila Gulyas⁴, Szabolcs Kali⁴, Michele Migliore¹, Rosanna Migliore¹, Maurizio Pezzoli⁵, Sara Sáray⁶, Luca Tar⁶, Daniel Schlingloff⁷, Peter Berki⁴, Tamas F. Freund⁴

¹Institute of Biophysics, National Research Council, Palermo, Italy; ²UCL School of Pharmacy, University College London, School of Pharmacy, London, United Kingdom; ³École Polytechnique Fédérale de Lausanne, Blue Brain Project, Lausanne, Switzerland; ⁴Institute of Experimental Medicine, Hungarian Academy of Sciences, Budapest, Hungary; ⁵Laboratory of Neural Microcircuitry (LNMC),Brain Mind Institute, EPFL, Lausanne, Switzerland; ⁶Hungarian Academy of Sciences and Pázmány Péter Catholic University, Institute of Experimental Medicine and Information Technology and Bionics, Budapest, Hungary; ⁷Hungarian Academy of Sciences and Semmelweis University, Institute of Experimental Medicine and János Szentágothai Doctoral School of Neurosciences, Budapest, Hungary

Correspondence: Paola Vitale (paola.vitale@pa.ibf.cnr.it)

BMC Neuroscience 2019, 20(Suppl 1):P86

Implementing morphologically and biophysically accurate single cell models, capturing the electrophysiological variability observed experimentally, is the first crucial step to obtain the building blocks to construct a brain region at the cellular level.

We have previously applied a unified workflow to implement a set of optimized models of CA1 neurons and interneurons of rats [1]. In this work, we apply the same workflow to implement detailed single cell models of CA1 and DG mouse neurons. An initial set of kinetic models and dendritic distributions of the different ion channels present on each type of cells studied neurons was defined, consistently with the available experimental data. Many electrophysiological features were then extracted from a set of experimental traces obtained under somatic current injections. For this purpose, we used the eFEL tool available on the Brain Simulation Platform of the HBP (https://collab.humanbrainproject.eu/#/collab/1655/nav/66850). Interestingly, for both cell types we observed rather different firing patterns within the same cell population, suggesting that a given population of cells in the mouse hippocampus cannot be considered as belonging to a single firing type. For this reason, we have chosen to cluster the experimental traces on the basis of the number of spikes as a function of the current injection and optimize each group independently from the others. We identified four different types of firing behavior for both DG’s granule cells and CA1’s pyramidal neurons. To create the optimized models, we used the BluePyOpt Optimization library [2] with several different accurate morphologies. Simulations were run on HPC systems at Cineca, Jülich, and CSCS. The results of the models for CA1 and DG will be discussed also in comparison with the models obtained for the rat.

References

1.
Migliore R, Lupascu CA, Bologna LL, et al. The physiological variability of channel density in hippocampal CA1 pyramidal cells and interneurons explored using a unified data-driven modeling workflow. PLoS computational biology 2018 Sep 17;14(9):e1006423.
2.
Van Geit W, Gevaert M, Chindemi G, et al. BluePyOpt: leveraging open source software and cloud infrastructure to optimize model parameters in neuroscience. Frontiers in neuroinformatics 2016 Jun 7;10:17.

P87 Memory compression in the hippocampus leads to the emergence of place cells

Marcus K. Benna, Stefano Fusi

Columbia University, Center for Theoretical Neuroscience, Zuckerman Mind Brain Behavior Institute, New York, NY, United States of America

Correspondence: Marcus K. Benna (mkb2162@columbia.edu)

BMC Neuroscience 2019, 20(Suppl 1):P87

The observation of place cells in the hippocampus has suggested that this brain area plays a special role in encoding spatial information. However, several studies show that place cells do not only encode position in physical space, but that their activity is in fact modulated by several other variables, which include the behavior of the animal (e.g. speed of movement or head direction), the presence of objects at particular locations, their value, and interactions with other animals. Consistent with these observations, place cell responses are reported to be rather unstable, indicating that they encode multiple variables, many of which are not under control in experiments, and that the neural representations in the hippocampus may be continuously updated. Here we propose a memory model of the hippocampus that provides a novel interpretation of place cells and can explain these observations. We hypothesize that the hippocampus is a memory device that takes advantage of the correlations between sensory experiences to generate compressed representations of the episodes that are stored in memory. We have constructed a simple neural network model that can efficiently compress simulated memories. This model naturally produces place cells that are similar to those observed in experiments. It predicts that the activity of these cells is variable and that the fluctuations of the place fields encode information about the recent history of sensory experiences. Our model also suggests that the hippocampus is not explicitly designed to deal with physical space, but can equally well represent any variable with which its inputs correlate. Place cells may simply be a consequence of a memory compression process implemented in the hippocampus.

P88 The information decomposition and the information delta: A unified approach to disentangling non-pairwise information

James Kunert-Graf, Nikita Sakhanenko, David Galas

Pacific Northwest Research Institute, Galas Lab, Seattle, WA, United States of America

Correspondence: James Kunert-Graf (kunert@uw.edu)

BMC Neuroscience 2019, 20(Suppl 1):P88

Neurons in a network must integrate information from multiple inputs, and how this information is encoded (e.g. redundantly between multiple sources, or uniquely by a single source) is crucial to the understanding of how neuronal networks transmit information. Information theory provides robust measures of the interdependence of multiple variables, and recent work has attempted to disentangle the different types of interactions captured by these measures (Fig 1A).

The Information Decomposition of Williams and Beer proposed decomposing the mutual information into unique, redundant, and synergistic components [1, 2]. This has been fruitfully applied, particularly in computational neuroscience, but there is no generally accepted method for its computation. Bertschinger et al. [3] developed one particularly rigorous approach, but it requires an intensive optimization over probability space (Fig 1B).

Independently, the quantitative genetics community has developed the Information Delta measures for detecting non-pairwise interactions for use in genetic datasets [4, 5, 6]. This has been exhaustively characterized for the discrete variables often found in genetics, yielding a geometric interpretation of how an arbitrary discrete function maps onto delta-space, and what its location therein encodes about the interaction (Fig 1C); however, this approach still lacks certain generalizations.

In this paper, we show that the Information Decomposition and Information Delta frameworks are largely equivalent. We identify theoretical advances in each that can be immediately applied towards answering questions open in the other. For example, we find that the results of Bertschinger et al. answer an open question in the Information Delta framework, specifically how to address the problem of linkage disequilibrium dependence in genetic data. We develop a method to computationally map the probability space defined by Bertschinger et al. into the space of delta measures, in which we can define a plane to which it is constrained with a well-defined optimum (Fig 1D). These optima occur at points in delta space which correspond to known discrete functions. This geometric mapping can thereby both side-step an expensive optimization and characterize the functional relationships between neurons. This unification of theoretical frameworks provides valuable insights for the analysis of how neurons integrate upstream information.

References

1.
Williams PL, Beer RD. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515.
2.
Lizier JT, Bertschinger N, Jost J, Wibral M. Information decomposition of target effects from multi-source interactions: Perspectives on previous, current and future work. Entropy 2018, 20, 307.
3.
Bertschinger N, Rauh J, Olbrich E, Jost J, Ay N. Quantifying unique information. Entropy 2014, 16, 2161–2183.
4.
Galas D, Sakhanenko NA, Skupin A, Ignac T. Describing the complexity of systems: Multivariable “set complexity” and the information basis of systems biology. J Comput Biol. 2014, 2, 118–140.
5.
Sakhanenko NA, Galas DJ. Biological data analysis as an information theory problem: Multivariable dependence measures and the shadows algorithm. J Comput Biol. 2015, 22, 1005–1024.
6.
Sakhanenko NA, Kunert-Graf JM, Galas DJ. The information content of discrete functions and their application in genetic data analysis. J Comp Biol. 2017, 24, 1153–1178.

P89 Homeostatic mechanism of myelination for age-dependent variations of axonal conductance speed in the pathophysiology of Alzheimer’s disease

Maurizio De Pittà¹, Giulio Bonifazi¹, Tania Quintela-López², Carolina Ortiz-Sanz², María Botta², Alberto Pérez-Samartín², Carlos Matute², Elena Alberdi², Adhara Gaminde-Blasco²

¹Basque Center for Applied Mathematics, Group of Mathematical, Computational and Experimental Neuroscience, Bilbao, Spain; ²Achucarro Basque Center for Neuroscience, Leioa, Spain

Correspondence: Giulio Bonifazi (gbonifazi@bcamath.org)

BMC Neuroscience 2019, 20(Suppl 1):P89

The structure of white matter in patients affected by Alzheimer’s disease (AD) and age-related dementia, typically reveals aberrant myelination, suggesting that ensuing changes in axonal conduction speed could contribute to cognitive impairment and behavioral deficits observed in those patients. Experiments ex vivo in a murine model of AD confirm these observations but also pinpoint to multiple, coexisting mechanisms that could intervene in regulation and maintenance of integrity of myelinated fibers. Density of myelinated fibers in the corpus callosum indeed appears not to be affected by disease progression in transgenic mice whereas density of myelinating oligodendrocyte is increased with respect to wild-type animals. Significantly, this enhancement correlates with an increased expression of myelin basic protein (MBP); as well as with nodes of Ranvier that are shorter and more numerous; and a decrease in axonal conduction speed. We show that these results can be reproduced by a classical model of action potential propagation in myelinated axons by the combination of three factors that are: (i) a reduction of node length in association with (ii) an increase of both internode number and (iii) myelin thickness. In the simple scenario of two interacting neural populations where a recently-observed inhibitory feedback on the degree of myelination is incorporated as a function of synaptic connection disrupted by extracellular amyloid beta oligomers (Aβ1-42), we show that the reduction of axonal conduction speed by the concerted increase of Ranvier’s node number and myelin thickness accounts for minimizing the energetic cost of interacting population activity.

P90 Collective dynamics of a heterogeneous network of active rotators

Pablo Ruiz, Jordi Garcia-Ojalvo

Universitat Pompeu Fabra, Department of Experimental and Health Sciences, Barcelona, Spain

Correspondence: Pablo Ruiz (pabloruizibarrechevea@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P90

We analyze the behavior of a network of active rotators [1] containing both oscillatory and excitable elements. We assume that the oscillatory character of the elements is continuously distributed. The system exhibits three main dynamical behaviors (i) a quiescent phase in which all elements are stationary, (ii) global oscillations in which all elements oscillate in a synchronized manner, and (iii) partial oscillations in which a fraction of the units oscillates, partially synchronized among them (analogous to the case in [2]). We also observe that the pulse duration is shorter for the excitable units than for the oscillating ones, even though the former has smaller intrinsic frequencies than the latter. Apart from the standard usage of the Kuramoto order parameter (or its variance) as a measure of synchrony, and consequently, as a measure of the macroscopic state of the system, we are interested in finding an observable that helps gain insight on what is the position within a hierarchy of states. We can call this measure the potential or energy of the system, and define it as the integral over the phases, by gradient dynamics [3]. This variable can be considered as a measure of multistability. We also study more complex coupling situations, included the existence of negative links between coupled elements in a whole-brain network, mimicking the inhibitory connections present in the brain.

References

1.
Sakaguchi H, Shinomoto S, Kuramoto Y. Phase transitions and their bifurcation analysis in a large population of active rotators with mean-field coupling. Progress of Theoretical Physics 1988 Mar 1;79(3):600–7.
2.
Pazó D, Montbrió E. Universal behavior in populations composed of excitable and self-oscillatory elements. Physical Review E 2006 May 31;73(5):055202.
3.
Ionita F, Labavić D, Zaks MA, Meyer-Ortmanns H. Order-by-disorder in classical oscillator systems. The European Physical Journal B 2013 Dec 1;86(12):511.

P91 A hidden state analysis of prefrontal cortex activity underlying trial difficulty and erroneous responses in a distance discrimination task

Danilo Benozzo¹, Giancarlo La Camera², Aldo Genovesio¹

¹Sapienza University of Rome, Department of Physiology and Pharmacology, Rome, Italy; ²Stony Brook University, Department of Neurobiology and Behavior, Stony Brook, NY, United States of America

Correspondence: Danilo Benozzo (danilo.benozzo@uniroma1.it)

BMC Neuroscience 2019, 20(Suppl 1):P91

Previous studies have established the involvement of prefrontal cortex (PFC) neurons in the decision process during a distance discrimination task. However, no single-neuron correlates of important task variables such as trial difficulty was found. Here, we perform a trial-by-trial analysis of ensembles of simultaneously recorded neurons, specifically, multiple single-unit data from two rhesus monkeys performing the distance discrimination task. The task consists in the sequential presentation of two visual stimuli (S1 and S2, in this order) separated by a temporal delay. The monkeys had to report which stimulus was farthest from a reference point after a GO signal consisting in the presentation of the same two stimuli in the two sides of the screen. Six stimulus distances were tested (from 8 to 48mm), generating five levels of difficulty, each measured as the difference |S2-S1| between the relative positions of the stimuli (difficulty increases with |S2-S1|).

We analyzed the neural ensemble data with a Poisson hidden Markov model (HMM). A Poisson-HMM describes the activity of each single trial by a sequence of vectors of firing rates across simultaneously recorded neurons. Each vector of firing rates is a metastable ‘state’ of the neural activity. HMM allows to identify changes in neural state independently of external triggers, which have previously been linked to states of attention, expectation and decision making, to name a few.

For each experimental session, we fit the HMM to the neural ensemble starting from random initial conditions and different numbers of states (between 2 and 5) using maximum likelihood (Baum-Welch algorithm). The fitting procedure was repeated 5 times with new random initial conditions until a convergence criterion was reached (capped at 500 iterations). The model with the smallest BIC was selected as the best model. Post-fitting, a state was assigned to each 5ms bin of data if its posterior probability given the data exceeded 0.8. To further avoid overfitting, only states exceeding 0.8 for at least 50 consecutive ms were kept.

First, we looked for a relationship between trial difficulty and the first state transition time after S2 presentation. We found that faster state transitions occurred in easier trials (Fig. 1a), but no correlation was found with first transition times after the GO signal. This demonstrates that task difficulty modulates the neural dynamics during decisions, and this modulation occurs in the deliberation phase and is absent when the monkeys convert the decision into action.

Second, we found that RTs were significantly longer in error trials compared to correct trials overall (p<0.001, t-test). Thus, we investigated the relationship between reaction times and neural dynamics. We focused on a larger time window, from 400 ms before S2 until the beginning of the following trial, in order to better capture the whole dynamics of state transitions. We found longer mean state durations after S2 in error trials compared to correct trials (Fig. 1b), a signature of a slowing down of cortical dynamics during error trials. The effect was largest in the period from S2 to the GO signal, i.e., during the deliberation period (2-way ANOVA, interaction term, p<0.001). These results indicate a global slowdown of the neural dynamics prior to errors as the neural substrate of longer reaction times during incorrect trials.

P92 Neural model of the visual recognition of social interactions

Mohammad Hovaidi-Ardestani, Martin Giese

Hertie Institute for Clinical Brain Research, Centre for Integrative Neuroscience, Department of Cognitive Neurology, University Clinic Tübingen, Tübingen, Germany

Correspondence: Mohammad Hovaidi-Ardestani (mohammad.hovaidi-ardestani@uni-tuebingen.de)

BMC Neuroscience 2019, 20(Suppl 1):P92

Humans are highly skilled at interpreting intent or social behavior from strongly impoverished stimuli [1]. The neural circuits that derive such judgements from image sequences are entirely unknown. It has been hypothesized that this visual function is based on high-level cognitive processes, such as probabilistic reasoning. Taking an alternative approach, we show that such functions can be accomplished by relatively elementary neural networks that can be implemented by simple physiologically plausible neural mechanisms, forming a hierarchical (deep) neural model of the visual pathway.

Methods: Extending classical biologically-inspired models for object and action perception [2, 3] and alternatively a front-end that exploits a deep learning model (VGG16) for the construction of low and mid-level feature detectors, we built a hierarchical neural model that reproduces elementary psychophysical results on animacy and social perception from abstract stimuli. The lower hierarchy levels of the model consist of position-variant neural feature detectors that extract orientation and intermediately complex shape features. The next-higher level is formed by shape-selective neurons that are not completely position-invariant, which extract the 2D positions and orientation of moving agents. A second pathway analyses the 2D motion of the moving agents, exploiting motion energy detectors. Exploiting a gain-field network, we compute the relative positions of the moving agents and analyze their relative motion. The top layers of the model combine the mentioned features that characterize the speed and smoothness of motion, and spatial relationships of the moving agents. The highest level of the model consists of neurons that compute the perceived agency of the motions, and that classify different categories of social interactions.

Results: Based on input video sequences, the model successfully reproduces results of [4] on the dependence of perceived animacy on motion parameters, and its dependence on the alignment of motion and body axis. The model reproduces the fact that a moving figure that with a body axis, like a rectangle, result in stronger perceived animacy than a moving circle if the body axis is aligned with the motion direction. In addition, the model classifies different interactions from abstract stimuli, including six categories of social interactions that have been frequently tested in the psychophysical literature (following, fighting, chasing, playing, guarding, and flirting) (e.g. [5, 6]).

Conclusion: Using simple physiologically plausible neural circuits, the model accounts simultaneously for a variety of effects related to animacy and social interaction perception. Even in its simple form the model proves that animacy and social interaction judgements partly can be derived by very elementary operations within a hierarchical neural vision system, without a need of sophisticated probabilistic inference mechanisms. The model makes precise predictions about the tuning properties of different types of neurons that should be involved in the visual processing of such stimuli. Such predictions might serve as starting point for physiological experiments that investigate the correlate of the perceptual processing of animacy and interaction at the single-cell level.

References

1.
Heider F, Simmel M. An experimental study of apparent behavior. The American journal of psychology 1944 Apr 1;57(2):243–59. https://doi.org/10.2307/1416950
2.
Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nature neuroscience 1999 Nov;2(11):1019. https://doi.org/10.1038/14819
3.
Giese MA, Poggio T. Cognitive neuroscience: neural mechanisms for the recognition of biological movements. Nature Reviews Neuroscience 2003 Mar;4(3):179. https://doi.org/10.1038/nrn1057
4.
Tremoulet PD, Feldman J. Perception of animacy from the motion of a single object. Perception 2000 Aug;29(8):943–51.
5.
Gao T, Scholl BJ, McCarthy G. Dissociating the detection of intentionality from animacy in the right posterior superior temporal sulcus. Journal of Neuroscience 2012 Oct 10;32(41):14276–80.
6.
McAleer P, Pollick FE. Understanding intention from minimal displays of human activity. Behavior Research Methods 2008 Aug 1;40(3):830–9. https://doi.org/10.3758/BRM.40.3.830

P93 Learning of generative neural network models for EMG data constrained by cortical activation dynamics

Alessandro Salatiello, Martin Giese

Center for Integrative Neuroscience & University Clinic Tübingen, Dept of Cognitive Neurology, Tübingen, Germany

Correspondence: Alessandro Salatiello (alessandro.salatiello@uni-tuebingen.de)

BMC Neuroscience 2019, 20(Suppl 1):P93

Recurrent Artificial Neural Networks (RNNs) are popular models for neural structures in motor control. A common approach to build such models is to train RNNs to reproduce the input-output mapping of biological networks. However, this approach suffers from the problem that the internal dynamics of such networks are typically highly under-constrained: even though they correctly reproduce the desired input-output behavior, their internal dynamics are not under control and usually deviate strongly from those of real neurons. Here, we show that it is possible to accomplish the dual goal of both reproducing the target input-output behavior and constraining the internal dynamics to be similar to the ones of real neurons. As a test-bed, we simulated an 8-target reaching task; we assumed that a network of 200 primary motor cortex (M1) neurons generates the necessary activity to perform such tasks in response to 8 different inputs and that this activity drives the contraction of 10 different arm muscles. We further assumed to have access to only a sample of M1 neurons (30%) and relevant muscles (40%). In particular, we first generated multiphasic EMG-like activity by drawing samples from a Gaussian process. Secondly, we generated ground truth M1-like activity by training a stability-optimized circuit (SOC) network [2] to reproduce the EMG activity through gain modulation [1]. Finally, we trained two RNN models with the full-FORCE method [3] to reproduce the subset of observed EMG activity; critically, while one of the networks (FF) was free to reach such a goal through the generation of arbitrary dynamics, the other (FFH) was constrained to do so by generating, through its recurrent dynamics, activity patterns resembling those of the observed SOC neurons. To assess the similarity between the activities of FF, FFH and SOC neurons, we applied canonical correlation analysis (CCA) on the latent factors extracted through PCA. This analysis revealed that while both the FF and FFH network were able to reproduce the EMG activities accurately, the FFH network, that is the one with constrained internal dynamics, showed a greater similarity in the neural response space with the SOC network. Such similarity is noteworthy since the sample used to constrain the internal dynamics was small. Our results suggest that this approach might facilitate the design of neural network models that bridge multiple hierarchical levels in motor control, at the same time including details of available single-cell data.

Acknowledgements: Funding from BMBF FKZ 01GQ1704, DFG GZ: KA 1258/15-1; CogIMon H2020 ICT-644727, HFSP RGP0036/2016, KONSENS BW Stiftung NEU007/1

References

1.
Stroud JP, Porter MA, Hennequin G, Vogels TP. Motor primitives in space and time via targeted gain modulation in cortical networks. Nature Neuroscience 2018 Dec;21(12):1774.
2.
Hennequin G, Vogels TP, Gerstner W. Optimal control of transient dynamics in balanced networks supports generation of complex movements. Neuron 2014 Jun 18;82(6):1394–406.
3.
DePasquale B, Cueva CJ, Rajan K, Abbott LF. full-FORCE: A target-based method for training recurrent networks. PloS One 2018 Feb 7;13(2):e0191527.

P94 A neuron can make reliable binary, threshold gate like, decisions if and only if its afferents are synchronized.

Timothee Masquelier¹, Matthieu Gilson²

¹CNRS, Toulouse, France; ²Universitat Pompeu Fabra, Center for Brain and Cognition, Barcelona, Spain

Correspondence: Timothee Masquelier (timothee.masquelier@cnrs.fr)

BMC Neuroscience 2019, 20(Suppl 1):P94

Binary decisions are presumably made by weighing and comparing evidence, which can be modeled using the threshold gate formalism: the decision depends on whether or not a weighted sum of input variables S exceeds a threshold θ. Incidentally, this is exactly how the first neuron model proposed by McCulloch and Pitts in 1943, and later used in the perceptron, worked. But can biological neurons implement such a function, assuming that the input variables are the afferent firing rates? This matter is unclear, because biological neurons deal with spikes, not firing rates.

We investigated this issue through analytical calculations and numerical simulations, using a leaky integrate-and-fire (LIF) neuron (with τ = 10 ms). The goal was to adjust the LIF’s threshold so that it fires at least one spike over a period T if S>θ (“positive condition”), and none otherwise (“negative condition”). We considered two different regimes: input spikes were either asynchronous (i.e., latencies were uniformly distributed over [0; T]), or synchronous. In the latter case, the spikes arrived in discrete periodic volleys (with frequency fo), and with a certain dispersion inside each volley (σ). As Fig. 1 Top shows, in the asynchronous regime any threshold will lead to false alarms and/or misses. Conversely, in the synchronous regime, it is possible to set a threshold that will be reached in the positive condition, but not in the negative one.

To demonstrate this more rigorously, we computed the receiver operating characteristic (ROC) curve as a function of T in both regimes (Fig. 1 Bottom). For the synchronous regime, we varied fo and σ. In short, the asynchronous regime leads to poor accuracy, which increases with T, but very slowly. Conversely, the synchronous regime leads to much better accuracy, which increases with T, but decreases with σ and fo.

In conclusion, if the decision needs to be taken in a reasonable amount of time, only the synchronous regime is viable, and the precision of the synchronization should be in the millisecond range. We are now exploring more biologically realistic regimes in which only a subset of the afferents is synchronized, in between the two extreme examples in Fig. 1. In the brain, the required synchronization could come from abrupt changes in the environment (e.g., stimulus onset), active sampling (e.g., saccades and microsaccades, sniffs, licking, touching), or endogenous brain oscillations. For example, rhythms in the beta or gamma ranges that correspond to different values for fo lead to different efficiency in our scheme for transmitting information, which implies constraints on the volley precision σ.

P95 Unifying network descriptions of neural mass and spiking neuron models and specifying them in common, standardized formats

Jessica Dafflon¹, Angus Silver², Padraig Gleeson²

¹King’s College London, Centre for Neuroimaging Sciences, London, United Kingdom; ²University College London, Dept. of Neuroscience, Physiology & Pharmacology, London, United Kingdom

Correspondence: Padraig Gleeson (p.gleeson@ucl.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P95

Due to the inherent complexity of information processing in the brain, many different approaches have been taken to creating models of neural circuits, each making different choices about the level of biological detail to incorporate and the mathematical/analytical tractability of the models. Some approaches favour investigating large scale, brain wide behaviour with interconnected populations, each representing the activity of many neurons. Others include many of the known biophysical details of the constituent cells, down to the level of ion channel kinetics. These different approaches often lead to disjointed communities investigating the same system from very different perspectives. There is also an important issue of different simulation technologies being used in each of these communities (e.g. The Virtual Brain; NEURON), further preventing exchange of models and theories.

To address these issues, we have extended the NeuroML model specification language [1, 2], which already supports descriptions of networks of biophysically complex, conductance based cells, to allow descriptions of population units where the average activity of the cells is given by a single variable. With this, it is possible to describe classic models such as that of Wilson and Cowan [3] in the same format as more detailed models. To demonstrate the utility of this approach we have converted a recent large-scale network model of the macaque cortex [4] into NeuroML format. This model features the interaction between the feedforward and feedback signalling across multiple scales. In particular, interactions inside cortical layers, between layers, between areas and at the whole cortex level are simulated. With the NeuroML implementation we were able to replicate the main findings described in the original paper.

Compatibility with NeuroML comes with other advantages, particularly the ability to visualise the structure of models in the format in 3D on Open Source Brain [5] as well as analyse the network connectivity and run and replay simulations (http://www.opensourcebrain.org/projects/mejiasetal2016). This extension to NeuroML for neural mass models, the support in compatible tools and platforms and example networks in this format will help enable sharing, comparison and reuse of models between researchers taking diverse approaches to understanding the brain.

References

1.
Cannon RC, Gleeson P, Crook S, Ganapathy G, Marin B, Piasini E, et al. LEMS: A language for expressing complex biological models in concise and hierarchical form and its use in underpinning NeuroML 2. Frontiers in neuroinformatics 2014;8. https://doi.org/10.3389/fninf.2014.00079
2.
Gleeson P, Crook S, Cannon RC, Hines ML, Billings GO, Farinella M, et al. NeuroML: A Language for Describing Data Driven Models of Neurons and Networks with a High Degree of Biological Detail. PLoS Comput Biol. Public Library of Science 2010;6: e1000815.
3.
Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12: 1–24.
4.
Mejias JF, Murray JD, Kennedy H, Wang X-J. Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Science advances 2016;2: e1601335.
5.
Gleeson P, Cantarelli M, Marin B, Quintana A, Earnshaw M, Piasini E, et al. Open Source Brain: a collaborative resource for visualizing, analyzing, simulating and developing standardized models of neurons and circuits. bioRxiv 2018; 229484.

P96 NeuroFedora: a ready to use Free/Open Source platform for Neuroscientists

Ankur Sinha¹, Luiz Bazan², Luis M. Segundo², Zbigniew Jędrzejewski-Szmek², Christian J. Kellner², Sergio Pascual², Antonio Trande², Manas Mangaonkar², Tereza Hlaváčková², Morgan Hough², Ilya Gradina², Igor Gnatenko²

¹University of Hertfordshire, Biocomputation Research Group, Hatfield, United Kingdom; ²Fedora Project

Correspondence: Ankur Sinha (a.sinha2@herts.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P96

Modern Neuroscience relies heavily on software. From the gathering of data, simulation of computational models, analysis of large amounts of information, to collaboration and communication tools for community development, software is now a necessary part of the research pipeline.

While the Neuroscience community is gradually moving to the use of Free/Open Source Software (FOSS) [11], our tools are generally complex and not trivial to deploy. In a community that is as multidisciplinary as Neuroscience, a large chunk of researchers hails from fields other than computing. It, therefore, often demands considerable time and effort to install, configure, and maintain research tool sets.

In NeuroFedora, we present a ready to use, FOSS platform for Neuroscientists. We leverage the infrastructure resources of the FOSS Fedora community [3] to develop a ready to install operating system that includes a plethora of Neuroscience software. All software included in NeuroFedora is built in accordance with modern software development best practices, follows the Fedora community’s Quality Assurance process, and is well integrated with other software such as desktop environments, text editors, and other daily use and development tools.

While work continues to make more software available in NeuroFedora covering all aspects of Neuroscience, NeuroFedora already provides commonly used Computational Neuroscience tools such as the NEST simulator [12], GENESIS [2], Auryn [8], Neuron [1], Brian (v1 and 2) [5], Moose [4], Neurord [10], Bionetgen [9], COPASI [6], PyLEMS [7], and others.

With up to date documentation atneuro.fedoraproject.org, we invite researchers to use NeuroFedora in their research and to join the team to help NeuroFedora better aid the research community.

References

1.
Hines ML, Carnevale NT. The NEURON simulation environment. Neural computation 1997 Aug 15;9(6):1179–209.
2.
Bower JM, Beeman D, Hucka M. The GENESIS simulation system, 2003.
3.
RedHat. Fedora Project, 2008.
4.
Dudani N, Ray S, George S, Bhalla US. Multiscale modeling and interoperability in MOOSE. BMC Neuroscience 2009 Sep;10(1):P54.
5.
Goodman DF, Brette R. The Brian simulator. Frontiers in neuroscience 2009 Sep 15; 3:26.
6.
Mendes P, Hoops S, Sahle S, et al. Computational modeling of biochemical networks using COPASI. Methods in molecular biology (Clifton, N.J.) 2009 500, 17–59. ISSN: 1064–3745.
7.
Vella M, Cannon RC, Crook S, et al. libNeuroML and PyLEMS: using Python to combine procedural and declarative modeling approaches in computational neuroscience. Frontiers in neuroinformatics 2014 Apr 23;8:38.
8.
Zenke F, Gerstner W. Limits to high-speed simulations of spiking neural networks using general-purpose computers. Frontiers in neuroinformatics 2014 Sep 11;8:76.
9.
Harris LA, Hogg JS, Tapia JJ, Sekar JA, Gupta S, Korsunsky I, Arora A, Barua D, Sheehan RP, Faeder JR. BioNetGen 2.2: advances in rule-based modeling. Bioinformatics 2016 Jul 8;32(21):3366–8.
10.
Jȩdrzejewski-Szmek Z, Blackwell KT. Asynchronous τ-leaping. The Journal of chemical physics 2016 Mar 28;144(12):125104.
11.
Gleeson P, Davison AP, Silver RA, Ascoli GA. A commitment to open source in neuroscience. Neuron 2017 Dec 6;96(5):964–5.
12.
Linssen C, Lepperød ME, Mitchell J, et al. NEST 2.16.0 Aug. 2018-08. https://doi.org/10.5281/zenodo.1400175.

P97 Flexibility of patterns of avalanches in source-reconstructed magnetoencephalography

Pierpaolo Sorrentino¹, Rosaria Rucco², Fabio Baselice³, Carmine Granata⁴, Rosita Di Micco⁵, Alesssandro Tessitore⁵, Giuseppe Sorrentino², Leonardo L Gollo¹

¹QIMR Berghofer Medical Research Institute, Systems Neuroscience Group, Brisbane, Australia; ²University of Naples Parthenope, Department of movement science, Naples, Italy; ³University of Naples Parthenope, Department of Engineering, Naples, Italy; ⁴National Research Council of Italy, Institute of Applied Sciences and Intelligent Systems, Pozzuoli, Italy; ⁵University of Campania Luigi Vanvitelli, Department of Neurology, Naples, Italy

Correspondence: Pierpaolo Sorrentino (ppsorrentino@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P97

Background: In many complex systems, when an event occurs, other units follow, giving rise to a cascade. The spreading of activity can be quantified by the branching ratio σ, defined by the number of active units at the present time over the one at the previous time step [1]. If σ = 1, the system is critical. In neuroscience, a critical system is believed to be more efficient [2]. For a critical branching, the system will visit a higher number of states [3]. Utilizing MEG recordings, we characterize patterns of activity at the whole brain level, and we compare the flexibility of patterns observed in healthy controls and Parkinson’s disease (PD). We hypothesize that the damages to the neuronal circuitry will move the network to a less efficient and flexible state, and that this may indicate clinical disability.

Methods: We recorded five minutes of closed eyes resting-state MEG in two cohorts: thirty-nine PD patients (20 males and 19 females, age 64.87 ± 9.12 years) matched with thirty-eight controls (19 males and 19 females, age 62.35 ± 8.74 years). The source-level time series of neuronal activity were reconstructed in 116 regions, by a beamformer approach based on the native MRI. The time series were filtered in the classical frequency bands. An avalanche was defined as a continuous sequence of time bins with activity on any region. T σ was estimated based on the geometric mean. We then counted the number of different patterns of avalanches that were present in each subject, and compared them between groups by permutation testing (Fig. 1). Finally, the clinical state was evaluated using the UPDRS-III scale. The relationship occurring between the number of patterns a patient visited and its clinical phenotype was assessed using linear correlation.

Results: Firstly, the analysis of sigma shows that MEG signals are in the critical state. Furthermore, the frequency band analysis showed that criticality is not a frequency-specific phenomenon. However, the contribution of each region to the avalanche patterns was frequency specific A comparison between healthy controls and PD patients shows that the latter tend to visit a lower number of patterns (for broad band p = 0.0086). The lower the number of visited patterns, the greater their clinical impairment.

Discussion: Here we put forward a novel way to identify brain states and quantify their flexibility. The contribution of regions to the diversity of patterns is heterogeneous and frequency specific, giving rise to frequency specific topologies Although the number of patterns of activity observed across participants is varied, we found that they are substantially reduced in the PD patients. Moreover, the amount of such reduction is significantly associated with the clinical disability.

References

1.
Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nature physics 2006 May;2(5):348.
2.
Cocchi L, Gollo LL, Zalesky A, Breakspear M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Progress in neurobiology 2017 Nov 1;158:132-52.
3.
Haldeman C, Beggs JM. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Physical review letters 2005 Feb 7;94(5):058101.

P98 A learning mechanism in cortical microcircuits for estimating the statistics of the world

Jordi-Ysard Puigbò Llobet¹, Xerxes Arsiwalla¹, Paul Verschure², Miguel Ángel González-Ballester³

¹Institute for Bioengineering of Catalonia, Barcelona, Spain; ²Institute for BioEngineering of Catalonia (IBEC), Catalan Institute of Advanced Studies (ICREA), SPECS Lab, Barcelona, Spain; ³UPF, ICREA, DTIC, Barcelona, Spain

Correspondence: Jordi-Ysard Puigbò Llobet (jysard@ibecbarcelona.eu)

BMC Neuroscience 2019, 20(Suppl 1):P98

We know that the brain can estimate what is the expected value of an input signal. Up to some extent, signals that differ slightly from this expectation will be ignored, whereas errors that exceed some particular threshold will unavoidably convey a behavioral or physiological response. In this work, we assume that this threshold should be variable and therefore dependent on the input uncertainty. Consequently, we present here a biologically plausible model of how the brain can estimate uncertainty in sensory signals. In the predictive coding framework, our model will attempt to assess the validity of sensory predictions and regulate learning accordingly. In this work, we use gradient ascent to derive the formulation that defines a dynamical system which provides estimations of input data while also estimating their variance. We start with the assumption that the probability of our sensory input being explained by internal parameters of the model and other external signals follows a normal distribution. Similar to the approach of [1], we minimize the error in predicting the input signal but, instead of fixing the standard deviation to one static value, we estimate the variance of the input online, as a parameter in our dynamical system. The resulting model is presented as a simple recurrent neural network in Fig. 1C (nodes change with the weighted sum of inputs and vertices follow Hebbian-like learning rules). This microcircuit becomes a model of how cortical networks use expectation maximization to estimate mean and variance of the input signals simultaneously (Fig. 1D). We carefully analyze the implications of estimating uncertainty in parallel to minimizing prediction error to observe that the computation of the variance results in the minimization of the relative error (absolute error divided by variance). While classical models of predictive coding assume the variance to be a fixed constant extracted from the data once, we observe that estimating the variance online increases considerably learning speed at the cost of sometimes converging to less accurate estimations (Fig. 1E). The learning process becomes more resilient to input noise than previous approaches while requiring accurate estimates of the expected input variance. We discuss that this system can be implemented under biological constraints. In that case, our model predicts that two different classes of inhibitory interneurons in the Neocortex must play a role in either estimating mean or variance and that external modulation of the variance-computing interneurons results in the modulation of learning speed, promoting the exploitation of existing models versus the adaptation of existing ones.

P99 Generalization of frequency mixing and temporal interference phenomena through Volterra analysis

Nicolas Perez Nieves, Dan Goodman

Imperial College London, Electrical and Electronic Engineering, London, United Kingdom

Correspondence: Nicolas Perez Nieves (np1714@ic.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P99

It has been recently shown that it is possible to use sinusoidal electric fields at kHz frequencies to enable focused, yet non-invasive, neural stimulation at depth by delivering multiple electric fields to the brain at slightly different frequencies (f1and f2) that are themselves too high to recruit effective neural firing, but for which the offset frequency is low enough to drive neural activity. This is called temporal interference (TI) [1]. However, it is not yet known the mechanism by which these electric fields are able to depolarise the cell membrane at the difference frequency despite the lack of depolarization by the individual kHz fields. There is some theoretical analysis into showing how neural stimulation at f1, f2<150Hz generates activity at the difference (f1-f2) and sum (f1+f2) of the frequencies due to the non-linearity of the spiking mechanism in neurons [2] via frequency mixing (FM). Yet, this approach is not general enough to explain why at higher frequencies we still see activity at the difference (f1-f2) with no activity present at any other frequency. To model the non-linearity present in neurons we propose using a Volterra expansion. First, we show that any non-linear system of order P when stimulated by N sinusoids will output a linear combination of sinusoids at frequencies given by all the possible linear combinations of the original frequencies with coefficients ±{0, 1, …, P}. This is consistent with [2] who give output frequencies at fout = nf1+mf2for n, m = ±{0, 1, 2}. We also show that the amplitude of each of the sinusoidal components at the output depends on the P-dimensional Fourier transforms of the Pth order kernel of the Volterra expansion evaluated at the stimulation frequencies (e.g. for a P = 2 system Ψ(±f{1, 2}, ±f{1, 2})) We simulate a population of leaky integrate and fire neurons stimulated by two sinusoidal currents at f1and f2and record the average population firing rate. For low frequencies (Fig. 1a), we see all combinations nf1+mf2as in [2]. For high frequencies (Fig. 1b), we only find f1-f2as in [1].

We then obtain the second order Volterra kernel using the Lee-Schetzen method [3]. The 2D Fourier transform of the kernel is shown in Fig. 1c. The dots show the 16 coefficients corresponding to |Ψ(±f{1, 2}, ±f{1, 2})|. As shown, for high stimulation frequencies, only the coefficients corresponding to f1-f2and the DC term are high enough to generate a response in the network, thus explaining TI stimulation. For low stimulation frequencies (<150Hz), all coefficients are high enough to produce a significant response at all nf1+mf2.

We have generalised previous experimental and theoretical results on temporal interference and frequency mixing. Understanding the mechanism of temporal interference stimulation will facilitate its clinical adoption, help develop improvement strategies and may reveal new computational principles of the brain.

References

1.
Grossman N, et al. Non-invasive Deep Brain Stimulation via Temporally Interfering Electric Fields. Cell 2017, Vol.169, Issue 6, pp.1029–1041.e16
2.
Haufler D, Pare D. Detection of Multiway Gamma Coordination Reveals How Frequency Mixing Shapes Neural Dynamics. Neuron 2019 Vol. 101, Issue 4, pp.603-614.e6
3.
van Drongelen, W. Signal Processing for Neuroscientists. Elsevier 2010, pp.39-90.

P100 Neural topic modelling

Pamela Hathway, Dan Goodman

Imperial College London, Department of Electrical and Electronic Engineering, London, United Kingdom

Correspondence: Pamela Hathway (p.hathway16@imperial.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P100

Recent advances in neuronal recording techniques have led to the availability of large datasets of neuronal activity. This creates new challenges for neural data analysis methods: 1) scalability to larger numbers of neurons, 2) combining data on different temporal and spatial scales e.g. single units and local field potentials and 3) interpretability of the results.

We propose a new approach to these challenges: Neural Topic Modelling, a neural data analysis tool based on Latent Dirichlet Allocation (LDA), a method routinely used in text mining to find latent topics in texts. For Neural Topic Modelling, neural data is converted into the presence or absence of discrete events (e.g. neuron 1 has a higher firing rate than usual), which we call “neural words”. A recording is split into time windows that reflect stimulus presentation (“neural documents”) and the neural words present in each neural document are used as input to LDA. The result is a number of topics—probability distributions over words—which best explain the given occurrences of neural words in the neural documents.

To demonstrate the validity of Neural Topic Modelling we analysed an electrophysiological dataset of visual cortex neurons recorded with a Neuropixel electrode. The spikes were translated into four simple neural word types: 1) increased firing rate in neuron i, 2) decreased firing rate in neuron i, 3) small inter-spike intervals in neuron i, 4) neurons i and j are simultaneously active.

Neural Topic Modelling identifies topics in which the neural words are similar in their preferences for stimulus location and brightness. Five out of ten topics exhibited a clear receptive field (RF)—a small region to which the words in the topic responded preferentially (positive RF, see Fig. 1 D) or non-preferentially (negative RF, see Fig. 1 C) as measured by weighted mean probabilities of the appearance of topic words given the stimulus location. The topic receptive fields overlap with the general mean probability of a word occurring given the stimulus location (see Fig. 1 A), but the topics responded to different subregions (see Fig. 1 B) and some were brightness-sensitive (see Fig. 1 D, right). Additionally, topics seem to reflect proximity on the recording electrode. We confirmed that topic groupings were not driven by word order or overall word count.

Neural Topic Modelling is an unsupervised analysis tool that receives no knowledge about the cortex topography nor about the spatial structure of the stimuli, but is nonetheless able to recover these relationships. The neural activity patterns used as neural words are interpretable by the brain and the resulting topics are interpretable by researchers. Converting neural activity into relevant events makes the method scalable to very large datasets and enables the analysis of neural data recordings on different spatial or temporal scales. It will be interesting to apply the model to more complex datasets e.g. in behaving mice, or to datasets where the neural representation of the stimulus structure is less clear e.g. for auditory or olfactory experiments.

The combination of scalability, applicability across temporal and spatial scales and the biological interpretability of Neural Topic Modelling sets this approach apart from other machine learning approaches to neural data analysis. We will make Neural Topic Modelling available to all researchers in the form of a Python software package.

P101 An attentional inhibitory feedback network for multi-label classification

Yang Chu, Dan Goodman

Imperial College London, Electrical Engineering, London, United Kingdom

Correspondence: Yang Chu (y.chu16@imperial.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P101

It’s not difficult for people to distinguish the sound of a piano and a bass in a jazz ensemble, or to recognize an actor under unique stage lighting, even if these combinations have never been experienced before. However, these multi-label recognition tasks remain challenging for current machine learning and computational neural models. The first challenge is to learn to generalize along with the combinatorial explosion of novel combinations, in contrast to brute-force memorization. The second challenge is to infer the multiple latent causes from mixed signals.

Here we present a new attentional inhibitory feedback model as a first step to address both these challenges and study the impact of feedback connections on learning. The new model outperforms baseline feedforward-only networks in an overlapping-handwritten-digits recognition task. Our simulation results also provide new understanding of feedback guided synaptic plasticity and complementary learning systems theory.

The task is to recognize two overlapping digits in an image (Fig 1A). The advantage of this for comparing neuro-inspired and machine learning approaches is that it is easy for humans but challenging for machine learning models, as they need to learn individual digits from combinations. Recognizing single handwritten digits, by contrast, can easily be solved by modern deep learning models.

The proposed model (Fig 1B) has a feature encoder built on a multi-layer fully connected neural network. Each encoder neuron receives an inhibitory feedback connection from a corresponding attentional neural network. During recognition, an image is first fed through the encoder, yielding a first guess. Then, based on the most confidently recognized digit, the attention module feeds back a multiplicative inhibitory signal to each encoder neuron. In the following time step, the image is processed again, but by the modulated encoder, resulting in a second recognition result. This feedback loop can carry on several times.

In our model, attention modulates the effective plasticity of different synapses based on the predicted contributions. While the attention networks learn to select more distinctive features, the encoder learns better with synapse-specific guidance from attention. Our feedback model achieves significantly higher accuracy comparing with the feedforward baseline network on both training and validation datasets (Fig 1C), despite having fewer neurons (2.6M compared to 3.7M). State of the art machine learning models can outperform our model but requires five to ten times as many parameters and more than a thousand times training data. Finally, we found intriguing dynamics during the co-learning process among attention and encoder networks, suggesting further links to neural development phenomena and memory consolidation in the brain.

Acknowledgements: This work was partly supported by a Titan Xp donated by the NVIDIA Corporation, and The Royal Society (grant RG170298).

P102 Closed-loop sinusoidal stimulation of ventral hippocampal terminals in prefrontal cortex preferentially entrains circuit activity at distinct frequencies

Maxym Myroshnychenko¹, David Kupferschmidt², Joshua Gordon³

¹National Institutes of Health, National Institute of Neurological Disorders and Stroke, Bethesda, MD, United States of America; ²National Institute of Neurological Disorders and Stroke, Integrative Neuroscience Section, Bethesda, MD, United States of America; ³National Institutes of Health, National Institute of Mental Health, Bethesda, United States of America

Correspondence: Maxym Myroshnychenko (mmyros@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P102

Closed-loop interrogation of neural circuits allows for causal description of circuit properties. Recent developments in recording and stimulation technology brought about the ability to stimulate or inhibit activity in one brain region conditional on the activity of another. Furthermore, the advent of optogenetics made it possible to control the activity of discrete, anatomically defined neural pathways. Normally, optogenetic excitation is induced using narrow pulses of light of the same intensity. To better approximate endogenous neural oscillations, we used continuously varied sinusoidal open- and closed-loop optogenetic stimulation of ventral hippocampal terminals in prefrontal cortex in awake mice. This allowed us to investigate the dynamical relationship between the two brain regions, which is critical for higher cognitive functions such as spatial working memory. Open-loop stimulation at different frequencies and amplitudes allowed us to map the response of the circuit over a range of parameters, revealing that response power in prefrontal and hippocampal field potentials was maximal in two tongue-shaped regions centered respectively at 8 Hz and 25–35 Hz, resembling resonant properties of coupled oscillators. Coherence between them was also maximal at these two frequency ranges. This suggests that neural activity in the circuit became entrained to the laser-induced oscillation, and the entrainment was not limited to the region near the stimulating laser. Further, adding frequency-filtered feedback based on the hippocampal field potential enhanced or suppressed synchronization depending on the amount of delay introduced to the feedback procedure. Specifically, delaying the optical stimulation relative to the hippocampal signal by about half of its period enhanced the entrainment of the prefrontal and hippocampal field potential responses to the stimulation frequency and enhanced prefrontal spikes’ phase locking to hippocampal field potential. On the other hand, closed-loop feedback without delay resulted in little enhancement and even decreased firing rate of prefrontal neurons. This is to our knowledge the first demonstration of an oscillatory phase-dependent bias in hippocampal-prefrontal communication based on an active closed-loop intervention. These results stand to inform computational models of communication between brain regions, and guide the use of continuously varying, closed-loop stimulation to assess effects of enhancing endogenous long-range neuronal communication on behavioral measures of cognitive function.

P103 The shape of thought: data-driven synthesis of neuronal morphology and the search for fundamental parameters of form

Joe Graham

SUNY Downstate Medical Center, Department of Physiology and Pharmacology, Brooklyn, NY, United States of America

Correspondence: Joe Graham (joe.w.graham@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P103

Neuronal morphology is critical in the form and function of nervous systems. Morphological diversity in and between populations of neurons contributes to functional connectivity and robust behavior. Morphologically-realistic computational models are an important tool in improving our understanding of nervous systems. Continual improvements in computing make large-scale, morphologically-realistic, biophysical models of nervous systems increasingly feasible. However, reconstructing large numbers of neurons experimentally is not scalable. Algorithmic generation of neuronal morphologies (“synthesis” of “virtual” neurons) holds promise for deciphering underlying patterns in branching morphology as well as meeting the increasing need in computational neuroscience for large numbers of diverse, realistic neurons.

There are many ways to quantify neuronal form, not all are useful. [1] proposed that “from the mass of quantitative information available” a small set of “fundamental parameters of form” and their intercorrelations could be measured from reconstructed neurons which could potentially “completely describe” the population. A parameter set completely describing the original data would be useful for classification of neuronal types, exploring embryological development of neurons, and for understanding morphological changes following illness or intervention. [2] realized that virtual dendritic trees could be generated by stochastic sampling from a set of fundamental parameters (a synthesis model). Persistent differences between the reconstructed and virtual trees guided model refinement. [3] realized entire virtual neurons could be created by synthesizing multiple dendritic trees from a virtual soma. [3] implemented the models of Hillman and Burke et al. and made the code and data publicly available. Both groups used the same data set: a population of six fully-reconstructed cat alpha motoneurons. They were able to generate virtual motoneurons that were similar to the reconstructed ones, however, persistent, significant differences remained unexplained.

Exploration of these motoneurons and novel synthesis models led to two major insights into dendritic form. 1) Parameter distributions correlate with local properties, and these correlations must be accounted for in synthesis models. Dendritic diameter is an important local property, correlating with most parameters. 2) Parent branch parameters correlate differently than those of terminal branches, requiring setting a branch’s type before synthesizing it. Inclusion of these findings in a synthesis model produces virtual motoneurons that are far more similar to the reconstructions than previous models and which are statistically indistinguishable across most measures. These findings hold true across a variety of neuronal types, and may constitute a key to the elusive “fundamental parameters of form” for neuronal morphology.

References

1.
Hillman DE. Neuronal shape parameters and substructures as a basis of neuronal form. In: The Neurosciences, 4th Study program. Cambridge: MIT Press; 1979, pp. 477–498.
2.
Burke RE, Marks WB, Ulfhake B. A parsimonious description of motoneuron dendritic morphology using computer simulation. Journal of Neuroscience 1992, 12(6), pp. 2403–2416.
3.
Ascoli GA, Krichmar JL, Scorcioni R, Nasuto SJ, Senft SL, Krichmar GL. Computer generation and quantitative morphometric analysis of virtual neurons. Anatomy and Embryology 2001 Oct 1;204(4):283–301.

P104 An information-theoretic framework for examining information flow in the brain

Praveen Venkatesh, Pulkit Grover

Carnegie Mellon University, Electrical and Computer Engineering, Pittsburgh, PA, United States of America

Correspondence: Praveen Venkatesh (vpraveen@cmu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P104

We propose a formal, systematic methodology for examining information flow in the brain. Our method is based on constructing a graphical model of the underlying computational circuit, comprising nodes that represent neurons or groups of neurons, which are interconnected to reflect anatomy. Using this model, we provide an information-theoretic definition for information flow, based on conditional mutual information between the stimulus and the transmissions of neurons. Our definition of information flow organically emphasizes what the information is about: typically, this information is encapsulated in the stimulus or response of a specific neuroscientific task. We also give pronounced importance to distinguishing the defining of information flow from the act of estimating it.

The information-theoretic framework we develop provides theoretical guarantees that were hitherto unattainable using statistical tools such as Granger Causality, Directed Information and Transfer Entropy, partly because they lacked a theoretical foundation grounded in neuroscience. Specifically, we are able to guarantee that if the “output” of the computational system shows stimulus-dependence, then there exists an “information path” leading from the input to the output, along which stimulus-dependent information flows. This path may be identified by performing statistical independence tests (or sometimes, conditional independence tests) at every edge. We are also able to obtain a fine-grained understanding of information geared towards understanding computation, by identifying which transmissions contain unique information and which are derived or redundant.

Furthermore, our framework offers consistency-checks, such as statistical tests for detecting hidden nodes. It also allows the experimentalist to examine how information about independent components of the stimulus (e.g., color and shape of a visual stimulus in a visual processing task) flow individually. Finally, we believe that our structured approach suggests a workflow for informed experimental design: especially, for purposing stimuli towards specific objectives, such as identifying whether or not a particular brain region is involved in a given task.

We hope that our theoretical framework will enable neuroscientists to state their assumptions more clearly and hence make more confident interpretations of their experimental results. One caveat, however, is that statistical independence tests (and especially, conditional independence tests) are often hard to perform in practice, and require a sufficiently large number of experimental trials.

P105 Detection and evaluation of bursts and rate onsets in terms of novelty and surprise

Junji Ito¹, Emanuele Lucrezia¹, Guenther Palm², Sonja Gruen^1,3

¹Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6), Jülich, Germany; ²University of Ulm, Institute of Neural Information Processing, Ulm, Germany; ³Jülich Research Centre, Institute of Neuroscience and Medicine (INM-10), Jülich, Germany

Correspondence: Junji Ito (j.ito@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P105

The detection of bursts and also of response onsets is often of relevance in understanding neurophysiological data, but the detection of these events is not a trivial task. Building on a method that was originally designed for burst detection using the so-called burst surprise as a measure [1], we extend it to a significance measure, the strict burst surprise [2, 3]. Briefly, the strict burst surprise is based on a measure called (strict) burst novelty, which is defined for each spike in a spike train as the greatest negative logarithm of the p-values for all ISI sequences ending at the spike. The strict burst surprise is defined as the negative logarithm of the p-value of the cumulative distribution function for the strict burst novelty. The burst detection method based on these measures consists of two stages as follows. In the first stage we model the neuron’s inter-spike interval (ISI) distribution and make an i.i.d. assumption to formulate our null hypothesis. In addition, we define a set of ‘surprising’ events that signify deviations from the null hypothesis in the direction of ‘burstiness’. Here the (strict) burst novelty is used to measure the size of this deviation. In the second stage we determine the significance of this deviation. The (strict) burst surprise is used to measure the significance, since it represents (the negative logarithm of) the significance probability of burst novelty values. We first show how a non-proper choice of null hypothesis affects burst detection performance, and then we apply the method to experimental data from macaque motor cortex [4, 5]. For this application the data are divided into a period for parameter estimation to express a proper null-hypothesis (model of the ISI distribution), and the rest of the data is analyzed by using that null hypothesis. We find that assuming a Poisson process for experimental spike data from motor cortex is rarely a proper null hypothesis, because these data tend to fire more regularly and thus a gamma process is more appropriate. We show that our burst detection method can be used for rate change onset detection (see Fig. 1), because a deviation from the null-hypothesis detected by (strict) burst novelty also covers an increase of firing rate.

References

1.
Legendy CR, Salcman M. Bursts and recurrences of bursts in the spike trains of spontaneously active striate cortex neurons. Journal of neurophysiology 1985 Apr 1;53(4):926–39.
2.
Palm G. Evidence, information, and surprise. Biological Cybernetics 1981 Nov 1;42(1):57–68.
3.
Palm G. Novelty, information and surprise. Springer Science & Business Media; 2012 Aug 30.
4.
Riehle A, Wirtssohn S, Grün S, Brochier T. Mapping the spatio-temporal structure of motor cortical LFP and spiking activities during reach-to-grasp movements. Frontiers in neural circuits 2013 Mar 27;7:48.
5.
Brochier T, Zehl L, Hao Y, et al. Massively parallel recordings in macaque motor cortex during an instructed delayed reach-to-grasp task. Scientific data 2018 Apr 10;5:180055.

P106 Precise spatio-temporal spike patterns in macaque motor cortex during a reach-to-grasp task

Alessandra Stella¹, Pietro Quaglio¹, Alexa Riehle², Thomas Brochier², Sonja Gruen¹

¹Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6 and INM-10), Jülich, Germany; ²CNRS - Aix-Marseille Université, Institut de Neurosciences de la Timone (INT), Marseille, France

Correspondence: Alessandra Stella (a.stella@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P106

The Hebbian hypothesis [1] states that neurons organize in assemblies of co-active neurons acting as information processing units. We hypothesize that assembly activity is expressed by the occurrence of precise spatio-temporal patterns (STPs) of spikes—with temporal delays between the spikes—emitted by neurons being members of the assembly. We developed a method, called SPADE [2, 3], that detects significant STPs in massively parallel spike trains. SPADE involves three steps: it first identifies repeating STPs using Frequent Itemset Mining [4]; second, it evaluates the detected patterns for significance; third, it removes the false positive patterns that are a byproduct of true patterns and background activity. SPADE is implemented in the Python library Elephant [5].

Here we aim to evaluate if cell assemblies are active in relation to motor behavior [6]. Therefore, we analyzed parallel spike data recorded in the pre-/motor cortex of a macaque monkey performing a reach-to-grasp task. The experimental paradigm is the following: after an instructed preparatory period, the monkeys had to pull and hold an object by using either a side or a precision grip, and using either high or low force (four behavioral conditions). We segmented the data into 500ms periods and analyzed them separately for the occurrence of STPs (an extension of [2]). We then registered for each significant STP its neuron composition, its number of occurrences and the times of the spikes involved in the pattern (see an example pattern in Fig. 1). This enabled us to investigate the time-resolved occurrences of each pattern across trials. Furthermore, we can make statistics of patterns’ characteristics in relation to the behavioral condition.

We find that STPs occur in all phases of the behavior, but are more frequent during the movement period. The patterns are specific to the behavioral conditions (different grip and force type combinations) during movement, suggesting that different assemblies are active for the performance of the different behavior. Interestingly, there is a high tendency that the same neurons participate in different STPs, however with different temporal lag constellations, i.e. as different STPs. This means that individual neurons are involved in different patterns at different points in time. These neurons may be interpreted as hub neurons [7]. We also find that individual spikes of some neurons may take part in different patterns. We are currently exploring if that indicates the existence of larger patterns, not detected because of our strict definition on the exact timing and constellation of spikes and neurons in the pattern. This may be too strict given the insights from modeling work [8].

References

1.
Hebb DO. The organization of behavior; a neuropsychological theory. A Wiley Book in Clinical Psychology 1949:62–78.
2.
Torre E, Quaglio P, Denker M, Brochier T, Riehle A, Grün S. Synchronous spike patterns in macaque motor cortex during an instructed-delay reach-to-grasp task. Journal of Neuroscience 2016 Aug 10;36(32):8329–40.
3.
Quaglio P, Yegenoglu A, Torre E, Endres DM, Grün S. Detection and evaluation of spatio-temporal spike patterns in massively parallel spike train data with spade. Frontiers in computational neuroscience 2017 May 24;11:41.
4.
Picado-Muiño D, Borgelt C, Berger D, Gerstein GL, Grün S. Finding neural assemblies with frequent item set mining. Frontiers in neuroinformatics 2013 May 31;7:9.
5.
Elephant - Electrophysiology Analysis Toolkit, http://www.python-elephant.org/, RRID:SCR_003833
6.
Brochier T, Zehl L, Hao Y, et al. Massively parallel recordings in macaque motor cortex during an instructed delayed reach-to-grasp task. Scientific data 2018 Apr 10;5:180055.
7.
Dann B, Michaels JA, Schaffelhofer S, Scherberger H. Uniting functional network topology and oscillations in the fronto-parietal single unit network of behaving primates. Elife 2016 Aug 15;5:e15719.
8.
Diesmann M, Gewaltig MO, Aertsen A. Stable propagation of synchronous spiking in cortical neural networks. Nature 1999 Dec;402(6761):529.

P107 Translating mechanisms of theta rhythm generation from simpler to more detailed network models

Alexandra Chatzikalymniou¹, Frances Skinner², Melisa Gumus³

¹Krembil Research Institute and University of Toronto, Department of Physiology, Toronto, Canada; ²Krembil Research Institute, Division of Fundamental Neurobiology, Toronto, Canada; ³Krembil Research Institute and University of Toronto, Institute of Medical Sciences, Toronto, Canada

Correspondence: Alexandra Chatzikalymniou (alex4@windowslive.com)

BMC Neuroscience 2019, 20(Suppl 1):P107

Theta oscillations in the hippocampus are important functional units for phase-coding in the brain [5]. However, how the interactions of the multiple inhibitory cell types and pyramidal cells give rise to these rhythms is far from clear. Recently, Bezaire and colleagues [1] built a full-scale CA1 hippocampus model with 8 inhibitory cell types and pyramidal cells using cellular, synaptic and connectivity characteristics based on a plethora of experimental data. Among other aspects, theirmodel identified interneuronal diversity and parvalbumin positive (PV) cell types as important factors for theta generation. In another recent modeling study [2], a network of PV fast-firing inhibitory and pyramidal cells revealed the importance of post-inhibitory rebound (PIR) as a network property requirement for the emergence of theta. As both models generated theta rhythms intrinsic to the hippocampus [3], we undertook comparisons to both leverage their advantages and overcome their limitations. An analysis of the Bezaire et al network model showed a consistency with the experimental excitatory/inhibitory current balances [4]. Also, the Ferguson et al model [2] predictions of connection probability requirements for theta, were consistent with the empirically determined connections in the Bezaire et al model [3]. Given this, we extracted a network `chunk’ of the later of a size similar to the model in [2], to facilitate comparisons and efficient computational investigations. Since it is known that the CA1 contains multiple theta generators across the septotemporal axis [3], our chunk network representsone of the many oscillators in this area. Without any model parameter adjustments, a chunk of the Bezaire et al no longer produces theta. After taking advantage of the balances exposed in the [2] model using high performance computing, we find that it is possible to generate theta in our chunk model. These rhythms occur preferentially for decreased pyramidal-pyramidal synaptic conductances relative to [1], suggesting that PIR plays a fundamental role in intrinsic theta. Moving forward, our models can be used to extract cell-type specific pathways critical for the theta rhythm.

References

1.
Bezaire MJ, Raikov I, Burk K, et al. Interneuronal mechanisms of hippocampal theta oscillations in a full-scale model of the rodent CA1 circuit. ELife Sciences 2016, 5, e18566.
2.
Ferguson KA, Chatzikalymniou AP, Skinner FK. Combining Theory, Model, and Experiment to Explain How Intrinsic Theta Rhythms Are Generated in an In Vitro Whole Hippocampus Preparation without Oscillatory Inputs. Eneuro. 2017,4 (4) ENEURO.0131-17.2017
3.
Goutagny R, Jackson J, Williams S. Self-generated theta oscillations in the hippocampus. Nature Neuroscience 2009, 12, 1491–1493.
4.
Huh CYL, Amilhon B, Ferguson KA, et al. Excitatory Inputs Determine Phase-Locking Strength and Spike-Timing of CA1 Stratum Oriens/Alveus Parvalbumin and Somatostatin Interneurons during Intrinsically Generated Hippocampal Theta Rhythm. Journal of Neuroscience 2016, 36, 6605–6622.
5.
Wilson MA, Varela C, Remondes M. Phase organization of network computations. Current Opinions Neurobiology 2015, 31: 250–253.

P108 NeuroViz: A web platform for visualizing and analyzing neuronal databases

Elizabeth Haynie¹, Kidus Debesai¹, Edgar Juarez Cabrera¹, Anca Doloc-Mihu², Cengiz Gunay¹

¹Georgia Gwinnett College, School of Science and Technology, Lawrenceville, United States of America; ²Georgia Gwinnett College, Information Technology/ SST, Decatur, GA, United States of America

Correspondence: Cengiz Gunay (cengique@users.sf.net)

BMC Neuroscience 2019, 20(Suppl 1):P108

Computer modeling of neuronal circuits has become a valuable tool in neuroscience. For a neuron model to be useful, its many free parameters need to be properly tuned using various exploration methods. These methods can illustrate a complete picture of all possible model outcomes and have been extremely valuable in understanding the principles of neuronal circuit function. These explorations yield large-scale neuron model simulation results databases, which provide opportunities for further investigations and new discoveries.

Many examples of such databases of simulation results already exist ([1, 2]; for a review, see [3]) and more will be available as new neuronal models are constructed and computing platforms get less expensive and more powerful. Simulation results databases are either publicly unavailable, or only available upon request [4]. However, the data are often stored in custom formats whose size increase exponentially with the number of parameters varied, making collaborations difficult. There is no central repository with a common format to store these databases. As computer simulation technologies and neuron models are advancing, parameter exploration methods are becoming more accessible to many researchers. Therefore, a common location to store and analyze model databases is needed more than ever.

To serve this need, we are proposing an online portal, called NeuroViz, which hosts neuronal simulation and recording databases. NeuroViz is planned to be an open freely available website where researchers can submit new model databases, and visualize and analyze existing databases. At first stage, we plan to provide only tabular data formats that contain parameter values and metrics already extracted from raw electrophysiology data. Here, we are presenting our initial designs of the software interface to validate and explore usage scenarios and receive feedback from potential users. Fig. 1 shows our first step into building this tool. For demonstration purposes, we have incorporated the HCO-DB [1] database from the leech.

References

1.
Doloc-Mihu A, Calabrese RL. A database of computational models of a half-center oscillator for analyzing how neuronal parameters influence network activity. Journal of biological physics 2011 Jun 1;37(3):263–83.
2.
Sekulić V, Lawrence JJ, Skinner FK. Using multi-compartment ensemble modeling as an investigative tool of spatially distributed biophysical balances: application to hippocampal oriens-lacunosum/moleculare (O-LM) cells. PLoS One 2014 Oct 31;9(10):e106567.
3.
Günay C. Neuronal model databases. Encyclopedia of Computational Neuroscience 2015:2024–8.
4.
Günay C, Prinz AA. Model calcium sensors for network homeostasis: sensor and readout parameter analysis from a database of model neuronal networks. Journal of Neuroscience 2010 Feb 3;30(5):1686–98.

P109 Computational analysis of disinhibitory and neuromodulatory mechanisms for induction of hippocampal plasticity

Ines Guerreiro¹, Zhenglin Gu², Jerrel Yakel², Boris Gutkin¹

¹École Normale Supérieure, Paris, France; ²NIEHS, Department of Health and Human Services, Research Triangle Park, United States of America

Correspondence: Ines Guerreiro (ines.completo@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P109

Since first observed in the rabbit hippocampus [1], LTP has remained a key subject of research, and the hippocampus continues to serve as a model structure for the study of plasticity. Studies of induction of hippocampal plasticity have shown that blockade of GABA inhibition can greatly facilitate the induction of LTP in excitatory synapses [2]. More specifically, recent studies show that repeated inhibition of hippocampal CA1 somatostatin-positive interneurons can induce lasting potentiation of Schaffer collateral (SC) to CA1 EPSCs, suggesting that repeated dendritic disinhibition of CA1 pyramidal cells plays a role in the induction of synaptic plasticity. It was also shown experimentally that repeated cholinergic activation enhanced the SC-evoked EPSCs through a7-containing nicotinic acetylcholine receptors (a7 nAChRs) expressed in oriens lacunosum-moleculare (OLMa2) interneurons. However, it is not clear how these circuits and neuromodulatory factors interplay to result in synaptic plasticity.

To analyse the plasticity mechanisms, first we used a biophysically-realistic computational model to examine mechanistically how inhibitory inputs to hippocampal pyramidal neurons can modulate the plasticity of the SC-CA1 excitatory synapses. We found that locally-reduced GABA release (disinhibition) could lead to increased NMDAR activation and intracellular calcium concentration sufficient to upregulate AMPAR permeability. Repeated disinhibition of the excitatory synapses could lead to larger and longer lasting increase of the AMPAR permeability, i.e. synaptic plasticity. We then used our model to show how repeated cholinergic activation of a7 nAChR in stratum oriens OLMa2 interneurons paired with SC stimulation can induce synaptic plasticity at the SC-CA1 excitatory synapses. Activation of pre-synaptic a7 nAChRs in OLM cells activates these interneurons which, in turn, inhibit fast-spiking stratum radiatum interneurons that provide feed-forward inhibition onto pyramidal neurons after SC excitation, and thus disinhibiting the CA1 pyramidal neurons. Repeated cholinergic activation then leads to repeated feed-forward disinhibition of the pyramidal cell, which can modulate the SC-CA1 synapses by the method previously described.

Our modelling work thus unravels the intricate interplay of the hierarchal inhibitory circuitry and cholinergic neuromodulation as a mechanism for hippocampal plasticity.

References

1.
Lømo T. Frequency potentiation of excitatory synaptic activity in the dentate area of the hippocampal formation. Acta Physiol. Scand 1966, 68(277), 128.
2.
Wingstrom H, Gustafsson B. Facilitation of hippocampal long-lasting potentiation by GABA antagonists. Acta Physiol. Scand 1985, 125, 159–172

P110 Coherence states of inter-communicating gamma oscillatory neural circuits

Gregory Dumont, Boris Gutkin

École Normale Supérieure, Paris, France

Correspondence: Gregory Dumont (gregory.dumont@ens.fr)

BMC Neuroscience 2019, 20(Suppl 1):P110

Macroscopic oscillations of different brain regions show multiple phase relationships that are persistent across time [3]. Such phase locking is believed to be implicated in a number of cognitive functions and is key to the so-called Communication Through Coherence theory for neural information transfer [3]. Multiple cellular level mechanisms influence the network dynamic and structure the macroscopic firing patterns. Key question is to identify the biophysical neuronal and synaptic properties that permit such motifs to arise and how the different coherence states determine the communication between the neural circuits. We use a semi-analytic approach to investigate the emergence of phase locking within two bidirectionally delayed-coupled spiking circuits with emergent global gamma oscillations. Internally the circuits consist of excitatory and inhibitory quadratic integrate-and-fire neurons coupled synaptically in an all-to-all fashion. Importantly the neurons are heterogeneous and are not all intrinsic oscillators. The circuits can show global pyramidal-interneuron or interneuron gamma rhythms. Using a mean-field approach and an exact reduction method [1, 4], we break down each gamma network into a low dimensional nonlinear system. We then derive the macroscopic phase resetting-curves (mPRCs) [1, 2] that determine how the phase of the global oscillation responds to incoming perturbations. We find that depending on the gamma type and perturbation target (excitatory of inhibitory neurons), the mPRC can be either class I (purely positive) or class II (by-phasic). We then study the emergence of macroscopic coherence states (phase locking) of two weakly synaptically-coupled gamma-networks. We derive a phase equation that links the synaptic mechanisms to the coherence state of the system; notably the determinant part played by the delay and coupling strength in the emergent variety of coherence modes. We show that the delay is a necessary condition for symmetry breaking, i.e. a non-symmetric phase lag between the macroscopic oscillations. We find that a whole host of phase-locking relationships exist, depending on the coupling strength and delay, potentially giving an explanation to the experimentally observations [8]. Our analysis, see Fig. 1, further allows us to understand how signal transfer between the gamma circuits may depend on the nature of their mutual coherence states [2].

Acknowledgement: This study was supported by the Russian Science Foundation grant (contract number: 17-11-01273).

References

1.
Dumont G, Ermentrout B, Gutkin B. Macroscopic Phase-resetting curves for spiking neural networks. Phys. Rev. E. 2017, 96,
2.
Dumont G, Gutkin B. Macroscopic Phase-resetting curves determine oscillatory coherence and signal transfer. arXiv:1812.03455[q-bio.NC] 2018
3.
Maris E, Fries P, van Ede F. Diverse phase relations among neuronal rhythms and their potential function. Trends in Neurosciences 2015 39(2), 86–99
4.
Montbrio E, Pazo D, Roxin A. Macroscopic description for networks of spiking neurons. Phys. Rev. X 2015, 5, 021,028

P111 Mechanisms of working memory stabilization by an external oscillatory input

Nikita Novikov¹, Boris Gutkin²

¹Higher School of Economics, Centre for cognition and decision making, Moscow, Russia; ²École Normale Supérieure, Paris, France

Correspondence: Nikita Novikov (nikknovikov@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P111

Working memory (WM) is the ability to retain information not currently presented from sensory systems. WM retention is accompanied by self-sustained elevation of firing rates, which is usually modelled as transition of a bistable system from the “background” to the “active” state after a brief stimulus presentation [1]. Besides firing rates, the beta oscillations are usually enhanced, supposedly stabilizing WM retention [2]. In this study, we propose mechanisms for such stabilization. Key to these mechanisms is that beta input could provide additional excitation due to non-linear properties of the neurons.

First, we identified the regimes where non-specific beta input affects more strongly populations in the active (memory) state, compared to the background state (due to their different resonant properties). We considered a system of two mutually inhibiting populations, one that (S) actively maintains a stimulus, and the other (D) is selective to a distractor and stays in the background state. Non-selective beta input to both populations provides stronger excitation to S (compared to D), impeding activation of D by the distractor and decreasing the chance that its presentation will erase the stimulus from WM (Fig. 1a, b).

Second, we considered models where the WM-holding population does not have a “true” attractor active state, but reacts to the stimulus by a slowly decaying firing rate increase. We found that an external beta input can provide enough excitation to make the memory retention stable (Fig. 1c) (similar mechanism was explored in [3]). Then we considered two such populations with excitatory coupling that could be considered as parts of a distributed single object representation. In the post-stimulus high firing rate regime, populations generate beta-band quasi-oscillations and could synchronize with certain probability, providing mutual excitation that supports stable joint activity (Fig. 1d,e). Weak external beta input to both populations increases the chance for synchronization, thus stabilizing WM retention (Fig. 1f).

We successfully tested the proposed mechanisms with the Wilson-Cowan-like population models. In summary, we demonstrated that WM retention could be stabilized by an external beta-band input via increasing competition between active and background populations, as well as via promoting cooperation between parts of a distributed active population. This is in line with the ideas that beta activity promotes status quo and helps forming of distributed functional ensembles in the cortex.

Acknowledgements: Supported by Russian Science Foundation grant (contract No: 17-11-01273).

References

1.
Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cerebral Cortex 1997, 7(3):237–252.
2.
Engel AK, Fries P. Beta-band oscillations - signaling the status quo? Current Opinion Neurobiology 2010, 20(2):156–165
3.
Schmidt H, Avitabile D, Montbrio E, Roxin A. Network mechanisms underlying the role of oscillations in cognitive tasks. PLoS Computational Biology 2018, 14(9):e1006430.

P112 Prediction of mean firing rate shift induced by externally applied oscillations in a spiking network model

Kristina Vodorezova¹, Nikita Novikov¹, Boris Gutkin²

¹Higher School of Economics, Center for Cognition and Decision Making, Moscow, Russia; ²École Normale Supérieure, Paris, France

Correspondence: Kristina Vodorezova (trustyourt@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P112

One presumable role of neural oscillations is stabilization or destabilization of neural codes, which promotes retention or updating of the encoded information, respectively [1, 2]. We hypothesize that such functions could stem from the ability of oscillations to differentially affect neural populations that actively retain information and those that stay in the background state [3]. To explore this mechanism, we considered a bistable excitatory-inhibitory network of leaky-integrate-and-fire (LIF) neurons with external sinusoidal forcing. The two steady states differ by their average firing rates and correspond to the active retention and to the background, respectively. We wanted to understand how periodic beta-band input affects time-averaged firing rates in both states. In order to systematically address this question, we developed a method for semi-numerical prediction of the oscillation-induced average firing rate shifts. We simulated single LIF neurons under various combinations of the input mean, variance, and oscillation amplitude. This time-consuming step was performed once; then its results were interpolated during the parameter space exploration. We considered a discrete grid in re-ri coordinates (time-averaged presynaptic excitatory and inhibitory firing rates, respectively). For each (re, ri) combination, we calculated the corresponding input mean and variance, as well as the linear response coefficient (input-output amplitude relation) for each population. Then, in a reverse-engineering way, we derived the amplitudes of the total (external + recurrent) oscillatory inputs. The pre-calculated data was used to determine the time-averaged postsynaptic firing rates (re1, ri1). The curves re = re1 and ri = ri1 defined the nullclines for the time-averaged forced system, and their intersections—the corresponding equilibria. In order to predict the stimulation effect, we visualized the nullclines both for the models with and without external periodic input (Fig. 1a). Using the described method, we found parameters, for which the oscillatory input produced an increase in the average firing rate of the excitatory population in the active memory state, but not in the background state. Our predictions were confirmed by spiking network simulations (Fig. 1b,c). Given the obtained results, we suggest that our method would be useful for further investigation of oscillatory control in multi-stable systems such as working memory or decision-making models.

Acknowledgements: Supported by a Russian Science Foundation grant (contract No: 17-11-01273).

References

1.
Engel AK, Fries P. Beta-band oscillations–signalling the status quo? Current opinion in neurobiology 2010;20(2):156–65.
2.
Brittain JS, Sharott A, Brown P. The highs and lows of beta activity in cortico-basal ganglia loops. The European journal of neuroscience 2014;39(11):1951–9.
3.
Schmidt H, Avitabile D, Montbrio E, Roxin A. Network mechanisms underlying the role of oscillations in cognitive tasks. PLoS computational biology 2018, 14(9):e1006430.

P113 Augmenting the source-level EEG signal using structural connectivity

Katharina Glomb¹, Joana Cabral², Margherita Carboni^3,4, Maria Rubega⁴, Sebastien Tourbier¹, Serge Vulliemoz^3,4, Emeline Mullier¹, Morten L Kringelbach⁵, Giannarita Iannotti⁴, Martin Seeber⁴, Patric Hagmann¹

¹Centre Hospitalier Universitaire Vaudois, Department of Radiology, Lausanne, Switzerland; ²University of Minho, Life and Health Sciences Research Institute, Braga, Portugal; ³University Hospital of Geneva, Geneva, Switzerland; ⁴University of Geneva, Department of Fundamental Neurosciences, Geneva, Switzerland; ⁵University of Oxford, Department of Psychiatry, Oxford, United Kingdom

Correspondence: Katharina Glomb (katharina.glomb@upf.edu)

BMC Neuroscience 2019, 20(Suppl 1):P113

Due to its high temporal resolution, EEG, in principle, can be used to characterize the dynamics of how remote brain regions communicate with each other on a millisecond scale. Recent advances have also made it possible to project the time series recorded at the scalp into the gray matter, localizing the sources of the activity. The main limitations one faces when analyzing such source-level time series are that the source signal has low SNR and spatial resolution and is polluted by volume conduction of the electromagnetic field between the sources. The latter leads to signals appearing functionally connected (i.e., statistically dependent) simply due to their proximity. Here we propose a new approach that addresses these issues: We combine source-level EEG data (resting state, 18 subjects) with structural connectivity (SC; number of streamlines found via diffusion imaging and fiber tracking). Thereby we exploit the fact that functional connectivity (FC) is partially mediated by anatomical white matter connections. We define a graph which consists of N nodes corresponding to N brain regions. Edges between nodes are defined by the SC. The source-projected activity measured at each point in time is taken to be the activity of the graph’s nodes over time. Each node in this graph has a set of nearest neighbors (NNs), i.e. nodes to which it is directly connected according to the SC, and we smooth our data using these NNs. In particular, for each point in time, a weighted average of each node’s NNs’ activity is added to its own activity. The contribution of the NNs is scaled by a factor G, controlling the level of smoothing. This procedure corresponds to convolving the electric signal with a low-pass filter, in graph space.

To test whether this method reduces the effects of volume conduction, we correlate EEG-FC to FC derived from fMRI, a method which does not suffer from volume conduction (fig. left). We compute envelope correlation-based EEG-FC matrices in three different frequency bands (alpha, beta, gamma; See Fig. 1, middle). We find that the EEG-FCs derived from smoothed data (fig. right) have a better fit to the fMRI-FC (0.28 vs 0.46 at G = 200). Importantly, the increase in fit is significantly stronger than when using NNs purely derived from Euclidean distance (Wilcoxon signed-rank test, corrected alpha = 0.05).

To further validate our technique, we fit the EEG-FCs to simulated data which are free of volume conduction effects. We use a network of N Kuramoto oscillators, coupled according to the empirical SC scaled by a global factor K. This model includes time delays tau, which are proportional to the length of the fibers connecting brain regions. We compute FCs from simulated data in the same way as from empirical data and assess the correlations between simulated and empirical FCs across a parameter space spanned by K and tau. Without filtering the empirical data, the maximum fit is 0.38; with filtering, this value increases to 0.49, again at G = 200. This is in line with the interpretation that graph filtering removes spurious correlations between nearby regions and boosts FC between far-away pairs of regions, demonstrating the merit of combining structural (SC) and functional data in EEG.

P114 Inferring birdsong neural learning mechanisms from behavior

Hazem Toutounji¹, Anja Zai¹, Ofer Tchernichovski², Dina Lipkind³, Richard Hahnloser¹

¹Institute of NeuroInformatics, UZH/ETH, Zurich, Switzerland; ²Hunter College, New York, United States of America; ³City University of New York, York College, New York, United States of America

Correspondence: Hazem Toutounji (hazem@ini.ethz.ch)

BMC Neuroscience 2019, 20(Suppl 1):P114

Learning complex skills requires continuous coordination between several behaviors. Juvenile male zebra finches, for instance, learn to produce songs by imitating the songs of adult male tutors. These songs consist of a sequence of syllables with distinct spectral features (e.g., pitch). The juvenile’s task is twofold: matching their syllable repertoire to the tutor’s (syllable assignment), and producing syllables in the right temporal order (syntax learning). It was previously shown that in learning a new song that involves both pitch and syntax change, juveniles first assign syllables to targets, followed by syntax learning [1]. Our work aims at identifying potential neural mechanisms of syllable assignment through data-driven computational modelling within reinforcement learning (RL) theory.

RL theory states that skill acquisition proceeds by learning the behaviors that maximize future rewards. This theoretical framework is often invoked as a working hypothesis for explaining songbird behavior when an aversive auditory stimulus is presented to an adult as reinforcement, but no formal models are yet developed in this context. Furthermore, dopaminergic neurons in the Ventral Tegmental Area (VTA) of adult songbird brains provide the learning signal necessary for escaping the aversive stimulus [2]. Juveniles, however, learn syllable assignment in the absence of external reinforcement, leading us to posit that an inner critic system drives learning during development. Sincedepleting dopamine in juveniles impairs tutor song learning [3], we suggest that the critic evaluates how well syllables in the juvenile’s repertoire match those in the target song.

Here we show that syllable assignment learning as observed experimentally [1] can be reproduced by assuming an intrinsic, global reward function that evaluates similarity in pitch between sung and target syllables. We develop an RL model in which an independent agent represents the motor program for each syllable pitch, assuming that both action and reward are continuous functions. Each agent aims at maximizing the global reward by adjusting its mean syllable pitch toward a target. We infer model parameters from one set of experimental data, including pitch and reward variances, and the time when a juvenile switches its attention toward a new target. Simulations with data-inferred parameters illustrate accurate qualitative agreement between data not involved in the fitting procedure and model. Finally, we make model-based, quantitative predictions on changes in dopaminergic VTA neuronal activity during juvenile song learning. These predictions are empirically verifiable and will be the basis for future investigations in the songbird brain.

Acknowledgments: Hazem Toutounji acknowledges the financial support of the German Academic Exchange Service (DAAD).

References

1.
Lipkind D, Zai, AT, Hanuschkin, A, et al. Songbirds work around computational complexity by learning song vocabulary independently of sequence. Nature Communications 2017, 8(1247).
2.
Gadagkar V, Puzerey PA, Chen R, et al. Dopamine neurons encode performance error in singing birds. Science 2016, 354(6317), 1278–1282.
3.
Hisey E, Kearney MG, Mooney, R. A common neural circuit mechanism for internally guided and externally reinforced forms of motor learning. Nature Neuroscience 2018 21(4), 589–597.

P115 A two-compartment neuron model with ion conservation and ion pumps

Marte J. Sætra¹, Gaute Einevoll², Geir Halnes²

¹University of Oslo, Department of Physics, Oslo, Norway; ²Norwegian University of Life Sciences, Faculty of Science and Technology, Aas, Norway

Correspondence: Marte J. Sætra (m.j.satra@fys.uio.no)

BMC Neuroscience 2019, 20(Suppl 1):P115

In most computational models of neurons, the membrane potential is the key dynamic variable. A common model assumption is that the intra- and extracellular concentrations of the main charge carriers (K+, Na+, Cl-) are effectively constant during the simulated period. On the time scale relevant for synaptic integration and the firing of a few action potentials (<1s), this is often a good approximation, since the transmembrane ion exchange is too small to impose significant concentration changes on this short timescale. The approximation is often valid also on a longer time scale due to the work done by uptake mechanisms (ion pumps and co-transporters) to restore baseline concentrations. However, in cases of neuronal hyperactivity or pump dysfunction, the re-uptake may become too slow, and ion concentrations may change over time. This occurs in several pathological conditions, including epilepsy, stroke and spreading depression.

To explore conditions involving shifts in ion concentrations, one needs neuron models that fully keep track of all ions and charges in the intra- and extracellular space. To accommodate this, we propose a version of the two-compartment (soma + dendrites) Pinsky-Rinzel model of a CA3 pyramidal cell [1], which is expanded so that it (i) includes two additional compartments for the extracellular space outside the soma and dendrite compartment, (ii) keeps track of all ion concentrations (K+, Na+, Cl- and Ca2+) in the intra- and extracellular compartments, and (iii) adds additional membrane mechanisms for ion pumps and co-transporters. The additional membrane mechanisms were taken from a previous model [2], and ion transports in the intra- and extracellular space were modelled using an electrodiffusive formalism that ensures ion conservation and a consistent relationship between ion concentrations and membrane voltages [3].

We tuned the new model aiming to preserve the characteristic firing properties of the original model, and at the same time obtain realistic ion-concentration dynamics, i.e., concentrations that remained close to physiological baseline values during normal working conditions, but diverged from baseline during neural hyperactivity. We analyzed the model by performing a sensitivity analysis using Uncertainpy [4]. With its reduced morphology, we envision that the model will be a useful building block in large network simulations of pathological conditions associated with ion concentration shifts in the extracellular space, such as stroke, spreading depression, and epilepsy.

References

1.
Pinsky PF, Rinzel J. Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. Journal of Computational Neuroscience 1994, 1(1–2):39–60.
2.
Wei Y, Ullah G, Schiff SJ. Unification of neuronal spikes, seizures, and spreading depression. Journal of Neuroscience 2014, 34(35):11733–11743.
3.
Halnes G, Østby I, Pettersen KH, Omholt SW, Einevoll GT. Electrodiffusive model for astrocytic and neuronal ion concentration dynamics. PLoS Computational Biology 2013, 9(12).
4.
Tennøe S, Halnes G, Einevoll GT. Uncertainpy: A Python toolbox for uncertainty quantification and sensitivity analysis in computational neuroscience. Frontiers in Neuroinformatics 2018, 12.

P116 Endogenously oscillating motoneurons produce undulatory output in a connectome-based neuromechanical model of C. elegans without proprioception

Haroon Anwar^1,2, Lan Deng², Soheil Saghafi³, Jack Denham⁴, Thomas Ranner⁴, Netta Cohen⁴, Casey Diekman³, Gal Haspel²

¹Princeton Neuroscience Institute, Princeton, NJ, United States of America; ²Federated Department of Biological Sciences, New Jersey Institute of Technology and Rutgers University - Newark; ³Department of Mathematical Sciences, New Jersey Institute of Technology, Newark; ⁴University of Leeds, School of Computing, Leeds, United Kingdom; ⁵New Jersey Institute of Technology, Mathematics Sciences, Newark, United States of America

Correspondence: Haroon Anwar (hanwar@njit.edu)

BMC Neuroscience 2019, 20(Suppl 1):P116

Neural circuits producing rhythmic behavior are often driven by pacemaker neurons. The endogenous pacemaker activity is often modulated by proprioceptive or descending signal. Although all the components of the compact locomotion circuit of Caenorhabditis elegans are identified and their connectivity has been deduced from electron micrographs, the neural mechanisms underlying rhythm generation and undulatory locomotion are still unknown. In C. elegans, undulation is produced by a propagation of alternating activation of 95 dorsal and ventral muscle cells along the animal body, opposite to the direction of movement. Past studies have mainly focused on two hypotheses: 1) Sensory feedback suffices to generate and propagate the rhythm: There are no pacemaker neurons and the neural circuit merely integrates over proprioceptive inputs to generate and propagate appropriate muscle activity [1, 2]. 2) Head oscillator model: A dorsoventral alternating pattern is generated in the neck by an oscillator, which drives the sensory feedback propagation along the animal [6-9]. Gjorgjieva et al [4] revisit a third hypothesis: Dorsoventral alternations are produced locally by oscillating pacemaker neurons and the orchestrations of appropriate phase relations are mediated by the finely tuned neuronal circuitry. In this study, we chose a computational approach to test the conditions for generation of locomotion patterns relying on pacemakers in the known connectivity in the absence of proprioceptive feedback.

We use our previously described neuromuscular network [5] that spans the full length of an animal and includes seven classes of motoneurons, muscle cells, and synaptic connections, both chemical and electrical. Using two kinds of motoneuron classes and muscle cells: leaky (passive) and endogenously oscillating (pacemaker), we systematically screened all 2^7 = 128 configurations of passive and pacemaker motoneuron classes. For each configuration, we screened parameter space and used parameter optimization approach to search for synaptic weights that produce a propagating dorsoventral alternation of muscular activity in forward or backward directions. The opposing directions of locomotion were induced by adding a tonic current to forward or backward motoneurons. We scored the dorsoventral alternation phases to evaluate simulation outputs, and used the same scoring algorithm on biological animals to assess biologically realistic undulation patterns. In the second stage, to see how fictive patterns translate in an embodied scenario, successful neuromuscular outputs were fed into a neuromechanical model [3] to test for realistic forward and backward locomotion.

When motoneuron classes were either all passive or all endogenous oscillators, an undulatory pattern in both forward and backward directions was not generated. We found that several configurations in which some excitatory motoneurons were oscillators produced undulatory-like activity pattern in both forward and backward directions. Moreover, implementation of these motor programs in the neuromechanical model produced multiple trajectories with varying speed and waveform, and clear wave propagation during both forward and backward locomotion depending on descending drive.

References

1.
Boyle JH, Berri S, Cohen N. Gait Modulation in C. elegans: An Integrated Neuromechanical Model. Frontiers in Computational Neuroscience 2012;6: 10. https://doi.org/10.3389/fncom.2012.00010
2.
Cohen N, Sanders T. Nematode locomotion: dissecting the neuronal-environmental loop. Current Opinions Neurobiology 2014; 25: 99–106. https://doi.org/10.1016/jconb.2013.12.003
3.
Denham JE, Ranner T, Cohen N. Signatures of proprioceptive control in Caenorhabditis elegans locomotion. Phil Trans Royal Society B. 2018; https://doi.org/10.1098/rstb.2018.0208
4.
Gjorgjieva J, Biron D, Haspel G. Neurobiology of Caenorhabditis elegans Locomotion: Where Do We Stand? BioScience 2014;64: 476. https://doi.org/10.1093/biosci/biu058
5.
Haspel G, O’Donovan MJ. A Perimotor Framework Reveals Functional Segmentation in the Motoneuronal Network Controlling Locomotion in Caenorhabditis elegans. Journal of Neuroscience 2011;31: 14611–14623. https://doi.org/10.1523/jneurosci.2186-11.2011
6.
Karbowski J, Schindelman G, Cronin CJ, Seah A, Sternberg PW. Systems level circuit model of C. elegans undulatory locomotion: mathematical modelling and molecular genetics. Journal of Computational Neuroscience 2008;24: 253–276. https://doi.org/10.1007/s10827-007-0054-6
7.
Kunert JM, Proctor JL, Brunton SL, Kutz JN. Spatiotemporal feedback and network structure drive and encode Caenorhabditis elegans locomotion. PLoS Computational Biology 2017; e1005303. https://doi.org/10.1371/journal.pcbi.1005303
8.
Niebur E, Erdös P. Theory of the locomotion of nematodes: control of the somatic motor neurons by interneurons. Mathematical Biosciences 1993;118: 51–82.
9.
Wen Q, Po MD, Hulme E, Chen S, Liu X, Kwok SW, et al. Proprioceptive Coupling within Motor Neurons Drives C. elegans Forward Locomotion. Neuron 2012;76: 750–761. https://doi.org/10.1016/j.neuron.2012.08.039

P117 Optimized reservoir computing with stochastic recurrent networks

Sandra Nestler, Chriastian Keup, David Dahmen, Moritz Helias

Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6), Jülich, Germany

Correspondence: Sandra Nestler (s.nestler@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P117

Cortical networks are strongly recurrent, and neurons have intrinsic temporal dynamics. This sets them apart from deep networks. Reservoir computing [1, 2] is an approach that takes these features into account. Inputs are here mapped into a high dimensional space spanned by a large number of typically randomly connected neurons; the network acts like a kernel in a support vector machine (Fig. 1). Functional tasks on the time-dependent inputs are realized by training a linear readout of the network activity.

It has been extensively studied how the performance of the reservoir depends on the properties of the recurrent connectivity; the edge of chaos has been found as a global indicator of good computational properties [3, 4].

However, the interplay of recurrence, nonlinearities, and stochastic neuronal dynamics may offer optimal settings that are not described by such global parameters alone. We here set out to systematically analyze the kernel properties of recurrent time-continuous stochastic networks in a binary time series classification task. We derive a learning rule that maximizes the classification margin. The interplay between the signal and neuronal noise determines a single optimal readout direction. Finding this direction does not require a training process; it can be directly calculated from the network statistics. This technique is reliable and yields a measure of linear separability that we use to optimize the remainder of the network. We show that the classification performance crucially depends on the input projection; random projections will lead to significantly suboptimal readouts.

We generalize these results to nonlinear networks. With field theoretical methods [5] we derive systematic corrections due to neuronal nonlinearities, which decompose the recurrent network into an effective bilinear time-dependent kernel. The expressions expose how the network dynamics separates a priori linearly non-separable time-series, and thus explain how recurrent nonlinear networks acquire capabilities beyond a linear perceptron.

Acknowledgements: Partly supported by HGF young investigator’s group VH-NG-1028 and European Union Horizon 2020 grant 785907 (Human Brain Project SGA2).

References

1.
Maass W, Natschlaeger T, Markram H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Computation 2002, 2531–2560.
2.
Jaeger H, Haas H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80
3.
Bertschinger N, Natschlaeger T, Legenstein R. At the Edge of Chaos: Real-time Computations and Self-Organized Criticality in Recurrent Neural Networks. Conference: Advances in Neural Information Processing Systems 17, 2005. (pp. 145–152).
4.
Toyoizumi T, Abbott L. Beyond the edge of chaos: Amplification and temporal integration by recurrent networks in the chaotic regime. Phys. Rev. E 2004, 84, 051908.
5.
Helias M, Dahmen D. Statistical field theory for neural networks. 2019, arXiv:1901.10416.

P118 Coordination between individual neurons across mesoscopic distances

David Dahmen¹, Moritz Layer¹, Lukas Deutz², Paulina Dabrowska^1,3, Nicole Voges^1,3, Michael von Papen^1,3, Sonja Gruen^1,4, Markus Diesmann^1,3, Moritz Helias¹

¹Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6), Jülich, Germany; ²University of Leeds, School of Computing, Leeds, Germany; ³Jülich Research Centre, Institute for Advanced Simulation (IAS-6), Jülich, Germany; ⁴Jülich Research Centre, Institute of Neuroscience and Medicine (INM-10), Jülich, Germany

Correspondence: David Dahmen (d.dahmen@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P118

The cortex is a network of networks that is organized on various spatial scales [1, 2]. On the largest scale, coordination of activity is mediated by specific white matter connectivity patterns of small-world character, allowing for short path lengths between any two cortical areas. In contrast, on the scale of small groups of neurons (<100 microns), connection patterns are seemingly random, offering the potential communication between any two cells. For the intermediate, mesoscopic scale inside a cortical area one finds that the majority of connections is governed by connection probabilities that fall off with distance on characteristic length scales of a few hundred microns. Neurons that are a few millimeters apart therefore most likely lack any synapse that would be required for coordination.

Yet, in massively parallel recordings of motor cortex spiking activity in awake and resting macaque monkey we find strongly correlated neurons almost across the whole Utah array, which covers an area of 4 × 4 mm². Positive and negative correlations form salt-and-pepper patterns in space that are seemingly unrelated to the underlying short-range connectivity profiles. Whilst additional complex connection and input structures could potentially give rise to such patterns, we here show that the latter emerge naturally in a dynamically balanced network near criticality [3] where interactions are mediated by a multitude of parallel paths through the network. As a consequence of multi-synaptic interactions via excitatory and inhibitory neurons, spatial profiles of correlations are much wider than those expected from structured connectivity, giving rise to long-distance coordination between individual cells. Using methods from statistical physics and disordered systems [4], we discover a relation between the distance to criticality and the spatial dependence of the statistics of correlations. For networks close to the critical point, individual neuron pairs show significant long-range correlations even though average correlations decay much faster than the connectivity. The operation point of the network, for example its overall firing rate, controls the spatial range on which neurons cooperate, thus offering a potential dynamic mechanism that adapts the circuit to different computational demands.

Acknowledgements: upported by HGF young investigator’s group VH-NG-1028 and European Union Horizon 2020 grant 785907 (Human Brain Project SGA2).

References

1.
Abeles M. Corticonics: Neural circuits of the cerebral cortex. Cambridge University Press, 1991.
2.
Braitenberg V, Schüz A. Cortex: statistics and geometry of neuronal connectivity. Springer Science & Business Media, 2013.
3.
Dahmen D, Grün S, Diesmann M, Helias M. Two types of criticality in the brain. arXiv, 1711.10930, 2017.
4.
Hertz JA, Roudi Y, Sollich P. Path integral methods for the dynamics of stochastic and disordered systems. Journal of Physics A: Mathematical and Theoretical 2017, 50(3):033001.

P119 Learning to learn on high performance computing

Sandra Diaz-Pier¹, Alper Yegenoglu², Wouter Klijn¹, Alexander Peyser¹, Wolfgang Maass³, Anand Subramoney⁴, Giuseppe Visconti⁴, Michael Herty⁴

¹Jülich Research Centre, SimLab Neuroscience, Jülich, Germany; ²Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6) & Institute for Advanced Simulation (IAS-6), Jülich, Germany; ³Graz University of Technology, Institute of Theoretical Computer Science, Graz, Austria; ⁴RWTH Aachen University, Institute of Geometry and Practical Mathematics, Department of Mathematics, Aachen, Germany

Correspondence: Sandra Diaz-Pier (s.diaz@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P119

Simulation of biological neural networks has become an essential part of neuroscience. The complexity of the structure and activity of the brain, combined with the limited access we have to measurements of in-vivo function of this organ, has led to the development of computational simulations which allows us to decompose, analyze and understand its elements and the interactions between them.

Impressive progress has recently been made in machine learning where brain-like learning capabilities can now be produced in non-spiking artificial neural networks [1, 3]. A substantial part of this progress arises from computing-intense learning-to-learn (L2L) [2, 4, 5] or meta-learning methods. L2L is a specific solution for acquiring constraints to improve learning performance.

The L2L conceptual world can be decomposed into an optimizee which learns specific tasks and an optimizer which searches for generalized hyperparameters for the optimizee. The optimizer learns to improve the optimizee’s performance over distinct tasks as measured by a fitness function (see Fig. 1).

In this work we present an implementation of L2L which works on High Performance Computing (HPC) [6] for hyperparameter optimization of spiking neural networks. First, we discuss how the software works on a supercomputing environment. Taking advantage of the large parallelization which can be achieved by deploying independent instances of the optimizees on HPC, our L2L framework becomes a powerful tool for understanding and analyzing mathematical models of the brain. We also present preliminary results on optimizing NEST simulations with structural plasticity using a variety of optimizer algorithms e.g. gradient descent, cross entropy, evolutionary strategies. Finally, we discuss initial results on optimization algorithms designed specifically to work with spiking neural networks.

The L2L framework is flexible and can be also used for finding optimal configurations of generic programs, not only neural network simulations. Because of this, it can be applied in and outside of neuroscience.

Acknowledgments: This work has been partially funded by the Helmholtz Association through the Helmholtz Portfolio Theme “Supercomputing and Modeling for the Human Brain”. In addition, this work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 720270 (HBP SGA1) and No 785907 (HBP SGA2).

References

1.
Lake BM, Ullman TD, Tenenbaum JB, Gershman SJ. Building machines that learn and think like people. Behavioral and brain sciences 2017;40.
2.
Thrun S, Pratt L, editors. Learning to learn. Springer Science & Business Media; 2012 Dec 6.
3.
Hutter F, Kotthoff L, Vanschoren J. Automatic machine learning: methods, systems, challenges. Springer 2018.
4.
Andrychowicz M, Denil M, Gomez S, et al. Learning to learn by gradient descent by gradient descent. In Advances in Neural Information Processing Systems 2016 (pp. 3981–3989).
5.
Jordan MI, Mitchell TM. Machine learning: Trends, perspectives, and prospects. Science 2015 Jul 17;349(6245):255–60.
6.
Subramoney A, Diaz-Pier S, Rao A, et al. (2019, March 11). IGITUGraz/L2L: v1.0.0-beta (Version v1.0.0-beta). Zenodo http://doi.org/10.5281/zenodo.2590760

P120 A novel method to encode sequences in a computational model of speech production

Meropi Topalidou, Emre Neftci, Gregory Hickok

University of California, Irvine, Department of Cognitive Sciences, Irvine, CA, United States of America

Correspondence: Meropi Topalidou (mtopalid@uci.edu)

BMC Neuroscience 2019, 20(Suppl 1):P120

The ability to sequence at the phoneme, syllable, and word level is essential to speech production. Speech production models generally contain buffers or working-memory modules to encode sequences [2, 4] or use slots to label the kind of the unit [3]. The goal of this work is to propose a simple computational model of speech production that produces sequences using a biological plausible method, but also it has reduced spatial and temporal complexity compared to the existing ones. We propose a novel method where the sequences are encoded by the synaptic weights of the network, a feature shared by many connectionist models. The organization of the model is derived from psycholinguistic models that propose a higher-level lexical (abstract word) system and a lower-level phonological system. Accordingly, the proposed computational model contains a lexical and a motor-phonological structures bidirectionally connected to each other. These components map onto the cortical regions of posterior superior temporal sulcus/middle temporal gyrus (pSTS/pMTG) for the lexical component, and posterior inferior frontal gyrus (pIFG) for the motor-phonological component. Additionally, the model contains an inhibitory mechanism that simulates the interneurons in pIFG. The basic idea of the model is that the ``word’’ at the lexical level, and its ``phonemes’’ at the motor level are connected by synaptic weights, where the first element of the sequence is more strongly connected with the word than the second one and so on. This is essentially equivalent to what Karl Lashley proposed in 1951; the serial order of the sequence is encoded into the activity level of each unit. The architecture of the model eliminates the need for buffers or position slots used by other models [2, 3].

Another advantage of our model is that it does not include a separate working memory to explicitly store symbolic information. Both layers include a winner-take-all mechanism to ensure that only one unit will remain active. However, the inhibitory mechanism is an essential part of the model for producing sequences. The role of this mechanism is to be a “puppet master” during the production of each phoneme by inhibiting the more active unit so the second more active unit will be expressed.

Saying it differently, each neuron representing a phoneme should stay active until the production has been completed, but be silent after. Analysis of the network behavior showed that with this simple architecture, the model is sufficient to produce any word as a sequence of phonemes. Furthermore, this method can be embedded in a broader model of sensorimotor planning for speech production. A limitation of the model is that cannot represent a sequence with duplicated elements; although, this can be overstepped by adding hierarchical organization at the lexical layer. For example, the lower level will include all the known syllables in the language, and in upper levels will include the combinations of these syllables to more complex words. The different levels at the lexical layer can be linked by using the same mechanism presented here.

References

1.
Hickok G. Computational neuroanatomy of speech production. Nature Reviews Neuroscience 2012 Feb;13(2):135.
2.
Bohland JW, Bullock D, Guenther FH. Neural representations and mechanisms for the performance of simple speech sequences. Journal of cognitive neuroscience 2010 Jul;22(7):1504–29.
3.
Foygel D, Dell GS. Models of impaired lexical access in speech production. Journal of Memory and Language 2000 Aug 1;43(2):182–216.
4.
Grossberg S. A theory of human memory: Self-organization and performance of sensory-motor codes, maps, and plans. In Studies of Mind and Brain 1982 (pp. 498–639). Springer, Dordrecht.
5.
Wilson DE, Smith GB, Jacob AL, et al. GABAergic neurons in ferret visual cortex participate in functionally specific networks. Neuron 2017 Mar 8;93(5):1058–65.

P121 Origin of 1/f^β noise structure in M/EEG power spectra

Rick Evertz¹, David Liley², Damien Hicks³

¹Swinburne University, Centre for Human Psychopharmacology, North Melbourne, Australia; ²University of Melbourne, Department of Medicine, Melbourne, Australia; ³Swinburne University, Department of Physics and Astronomy, Hawthorn, Australia

Correspondence: Rick Evertz (revertz@swin.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P121

Spectral analysis of magneto/electroencephalography (M/EEG) time series presents with a clearly pronounced alpha-band peak followed by a distinct S(f) = 1/f^β noise profile. The mechanistic origin of the alpha peak and its progenitor oscillation is an unresolved question in M/EEG research often thought to be dynamically unrelated to the S(f) = 1/f^β noise structure present in power spectra. Assuming that the measured M/EEG power spectrum can be modeled as a superposition of alpha-band relaxation processes with a distribution of dampings, the origin of the alpha peak and S(f) = 1/f^β noise profile can thus be explained via a singular generative mechanism. Within this framework, changes to the alpha peak and spectral noise profile are hypothesized to be a consequence of changes in the underlying damping distribution. We estimated the damping distributions for M/EEG power spectra computed from time series data that was recorded for multiple participants across a range of conditions. In practice this required solving a Fredholm integral equation of the first kind which was achieved through the use of second order Tikhonov regularization. The estimated damping distributions shared several robust features across multiple participants. The damping distributions were found to be multimodal with changes in EEG alpha peak between eyes closed and eyes open resting state, the result of a shift in the first mode of the distributions to a more heavily damped mode. The same were found for MEG power spectra where reductions in the alpha peak between resting and anesthesia (Xenon) states were observed. The shift in the most weakly damped distribution mode to more heavily damped one resulted in a direct reduction in the alpha peak. Furthermore, the bulk S(f) = 1/f^β properties of the M/EEG power spectra was replicated by using the regularized damping distributions in the forward model to generate an estimated power spectrum which fit the measured data remarkably well. The results demonstrate that the alpha peak and the S(f) = 1/f^β noise profile can be explained by a singular mechanism and changes to the spectral properties are a direct consequence of changes in the underlying damping distributions.

P122 A neural mechanism for predictive optokinetic eye movement

Ruben-Dario Pinzon-Morales, Shuntaro Miki, Yutaka Hirata

Chubu University, Robotics Science and Technology, Kasugai, Aichi, Japan

Correspondence: Yutaka Hirata (yutaka@isc.chubu.ac.jp)

BMC Neuroscience 2019, 20(Suppl 1):P122

This work deals with a sufficient mechanism for reproducing predictive eye velocity control known as predictive optokinetic response (OKR).

P123 Evaluation of context dependency in VOR motor learning using artificial cerebellum

Shogo Takatori, Keiichiro Inagaki, Yutaka Hirata

Chubu University, Robotics Science and Technology, Kasugai, Aichi, Japan

Correspondence: Shogo Takatori (tr18009-0255@sti.chubu.ac.jp)

BMC Neuroscience 2019, 20(Suppl 1):P123

The vestibuloocular reflex (VOR) maintains stable vision during head motion by counter rotating the eyes in the orbit. The VOR has been a popular model system to investigate neural mechanism of motor learning as its gain defined as eye velocity / head velocity is easily modifiable by visual-vestibular mismatch stimuli. When visual stimulation is given in-phase or out-of-phase with head motion for 10 min or longer, VOR gain measured in darkness w/o visual stimulation decreases or increases, respectively. As many other biological adaptive motor control systems, VOR motor learning is context dependent [1]. For example, VOR gain increase and decrease can be induced simultaneously for different head rotation directions. Namely, by applying visual stimulus out-of-phase with leftward head rotation and in-phase with rightward head rotation (L-Enh/R-Sup stimulus), VOR gain in dark during left and rightward head rotation respectively increases and decreases. It has been shown that long-term depression (LTD) and long-term potentiation (LTP) at the parallel fiber (PF)–Purkinje cell (PC) synapses in the cerebellum play major roles in VOR motor learning. However, how cerebellar neuronal circuitry incorporating those LTD and LTP achieves head direction dependent VOR motor learning is still unknown. Presently, we investigated the effect of directional context in the VOR motor learning, using the artificial cerebellum that we have been developing and modifying for the past decade [2]. Our artificial cerebellum having a bihemispheric structure was utilized for simulations of head direction dependent VOR motor learning. For that, the non-cerebellar neural pathways subserving VOR are described by transfer functions based on physiological experimental results in squirrel monkey. The cerebellar flocculus neuronal network was constructed based on the known anatomical and physiological evidence by spiking neuron models. LTD and LTP between PF–PC were described in spike timing dependent plasticity. Directional dependent VOR motor learning was induced in the model after 2-hour L-Enh/R-Sup training. A simple possible mechanism to achieve this head direction selective VOR motor learning is that the cerebellar left hemisphere is responsible for VOR gain increase during leftward head rotation and the right hemisphere is for gain decrease during rightward rotation. We showed that this scenario is unlikely because substituting PF-PC synaptic weights in the left hemisphere with those acquired by ordinary VOR gain increase training and those in the right hemisphere with those after ordinary gain decrease training did not reproduce the directional dependent VOR gain changes. These results suggest that the need of learning of directional context to achieve directional context dependent VOR gain change. Our results also indicated that mechanism for context dependent VOR motor learning differs from ordinary VOR gain increase and decrease learning.

Acknowledgement: A part of this work was supported by JSPS KAKENHI Grant Number 17K12781.

References

1.
Yoshikawa A, Hirata Y. Different mechanisms for gain-up and gain-down vestibuloocular reflex motor learning revealed by directional differential learning tasks. The IEICE transactions on information and systems 2009, J92-D, pp.176–185.
2.
Takatori S, Inagaki K, Hirata Y. Realization of direction selective motor learning in the artificial cerebellum: simulation on the vestibuloocular reflex adaptation. IEEE EMBC 2018.

P124 A computational model of the spontaneous activity of gonadotropin-releasing cells in the teleost fish medaka

Geir Halnes¹, Simen Tennøe², Gaute Einevoll¹, Trude M. Haug³, Finn-Arne Weltzien⁴, Kjetil Hodne⁴

¹Norwegian University of Life Sciences, Faculty of Science and Technology, Aas, Norway; ²University of Oslo, Department of Informatics, Oslo, Norway; ³University of Oslo, Institute of Oral Biology, Oslo, Norway; ⁴Norwegian University of Life Sciences, Department of Basic Sciences and Aquatic Medicine, Aas, Norway

Correspondence: Geir Halnes (geih@nmbu.no)

BMC Neuroscience 2019, 20(Suppl 1):P124

Pituitary hormone producing gonadotrope cells can fire spontaneous action potentials (APs). The hormone-release rate is proportional to the cytosolic Ca2+ concentration, which is regulated by release from intracellular stores (ER), and/or influx through Ca2+ channels on the plasma membrane. While ER-Ca2+ release normally requires G-protein activation, Ca2+ influx through the plasma membrane relies largely on the intrinsic firing properties of the cell. The spontaneous activity is partly important for the re-filling of ER, but may also give rise to a basal hormone secretion rate [1]. Pituitary APs are typically generated by TTX-sensitive Na+ currents (INa), high-voltage activated Ca2+ currents (ICa), or by a combination of the two [1]. Previous computational models have focused on conditions where spontaneous APs are predominantly mediated by ICa. This is representative for many pituitary cells, but not all (see [2] and refs. therein).

Here, we present a computational model of a gonadotrope cell in the teleost fish medaka, which fire INa-dependent spontaneous APs. The model contains a leak conductance, two depolarizing channels (INa and ICa) that mediate the AP upstroke, and three hyperpolarizing K+-channels that shape the downstroke of the AP. The leakage- and K+- channels were adapted from a previous study [3], while the kinetics of INa and ICa were adapted to new voltage-clamp data. The channel conductances were constrained to current-clamp recordings under control conditions, after TTX application, and after application of the BK-channel blocker paxilline. We compare the model to previous pituitary cell models (based on data from rats and mice), and perform a sensitivity analysis of the model by using the toolbox UncertainPy [4]. Although the model was constrained to experimental data from gonadotrope cells in medaka, we anticipate that modified versions of it will be useful for describing also other pituitary cells that fire INa-mediated APs.

Acknowledgements: This work was funded by the Research Council of Norway via the BIOTEK2021 project “DigiBrain”, grant no 248828, and the Aquaculture program, grant no 244461.

References

1.
Stojilkovic SS, Tabak J, Bertram R. Ion channels and signaling in the pituitary gland. Endocrine reviews 2010 Dec 1;31(6):845–915.
2.
Halnes G, Tennøe S, Haug TM, Einevoll GT, Weltzien FA, Hodne K. BK channels have opposite effects on sodium versus calcium-mediated action potentials in endocrine pituitary cells. bioRxiv 2018 Jan 1:477976.
3.
Tabak J, Tomaiuolo M, Gonzalez-Iglesias AE, Milescu LS, Bertram R. Fast-activating voltage-and calcium-dependent potassium (BK) conductance promotes bursting in pituitary cells: a dynamic clamp study. Journal of Neuroscience 2011 Nov 16;31(46):16855–63.
4.
Tennøe S, Halnes G, Einevoll GT. Uncertainpy: A Python toolbox for uncertainty quantification and sensitivity analysis in computational neuroscience. Frontiers in neuroinformatics 2018;12.

P125 Neural transmission delays and predictive coding: Real-time temporal alignment in a layered network with Hebbian learning

Anthony Burkitt¹, Hinze Hogendoorn²

¹University of Melbourne, Department of Biomedical Engineering, Melbourne, Australia; ²University of Melbourne, Melbourne School of Psychological Sciences, Melbourne, Australia

Correspondence: Anthony Burkitt (aburkitt@unimelb.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P125

The transmission of information in neural systems inherently involves delays, which results in our awareness of sensory events necessarily lagging behind the occurrence of those events in the world. In the absence of some mechanism to compensate for these delays, our visual perception would consistently mislocalize moving objects behind their actual position. Anticipatory mechanisms that might compensate for these delays have been hypothesized to underlie perceptual effects in humans such as the Flash-Lag Effect. However, there has been no consistent neural modelling framework that captures these phenomena.

By extending the predictive coding framework to take account of the delays inherent in neural transmission, we have proposed a real-time temporal alignment hypothesis [1]. In this framework both the feed-forward and feedback extrapolation mechanisms realign the feedback predictions to minimize prediction error. The consequence is that neural representations across all hierarchical stages become aligned in real-time.

In order to demonstrate real-time temporal alignment in a layered network of neurons, we consider a network architecture in which the location of a moving stimulus is encoded at each layer of the network by a population code for both the position and velocity of the stimulus. There are N position sub-populations at each layer, each with an identical Gaussian distribution and each containing M velocity sub-populations. The sub-populations are connected by both feed-forward and feedback weights. The excitatory feed-forward weights between the neural populations at each layer and subsequent layer are learned by a Hebbian rule and normalization is imposed.

Using this model, we explore the key mechanisms of neural coding and synaptic plasticity necessary to generate real-time alignment of neural activityin a layered network. We demonstrate how a moving stimulus generates a representation of the position and velocity of the stimulus in the higher levels of the network that maintains the real-time representation of the stimulus, accounting for the neural processing delay associated with the transmission of information through the network. This neural population code alignment provides a solution to the temporal binding problem, since the neural population activity remains in real-time temporal alignment with the moving stimulus that generates the input to the network. Second, we show that this real-time population neural code can prime the appropriate neural sub-population that is consistent with a constantly moving stimulus. This priming of the neural activity in alignment with a moving stimulus provides a parsimonious explanation for several known motion-position illusions [2].

In summary, this study uses visual motion as an example to illustrate a neurally plausible model of real-time temporal alignment. This model is consistent with evidence of extrapolation mechanisms throughout the visual hierarchy, it predicts several known motion-position illusions in human observers, and that it provides a solution to the temporal binding problem.

References

1.
Hogendoorn H, Burkitt AN. Predictive coding with neural transmission delays: a real-time temporal alignment hypothesis. bioArxiv 2018, doi:http://dx.doi.org/10.1101/453183
2.
Hogendoorn H, Burkitt AN. Predictive coding of visual object position ahead of moving objects revealed by time-resolved EEG decoding, NeuroImage 2018 171: 55–61.

P126 Emergence of ‘columnette’ orientation map in mouse visual cortex

Peijia Yu, Brent Doiron, Chengcheng Huang

University of Pittsburgh, Department of Mathematics, Pittsburgh, PA, United States of America

Correspondence: Peijia Yu (yupeijia.qbio@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P126

The orientation selectivity of neurons in the primary visual cortex (V1) of higher mammals, such as primates and cats, are spatially arranged in columnar maps. In contrast, the V1 of rodents are believed to have no clear spatial organization, and rather form a ‘salt-and-pepper’ style organization. However, [1] recently showed that the tuning similarity of pyramidal neurons in mouse V1 decreases with cortical distance, indicating a weak spatial clustering of tuning, instead of a strict salt-and-pepper map (Fig. 1a) [1].

To study the emergence of spatial organization of orientation tuning, we model the layer (L) 4 and layer (L) 2/3 of rodent V1 with a network of spiking neurons (Fig. 1b). The tuning curves of L4 neurons are homogeneous, with preferred orientations randomly assigned without any spatial correlation (i.e. ‘salt-and-pepper’). The L2/3 network consists of excitatory and inhibitory neurons receiving feedforward input from L4 neurons, and lateral recurrent inputs. The probability of both feedforward and recurrent connectivity decays with physical distance, which obey 2D Gaussian-shaped function with average widths alpha_F and alpha_R, respectively.

We found that when the network has strong, yet balanced, excitatory and inhibitory interactions, even though feedforward and recurrent inputs to L2/3 neurons are weakly tuned due to spatial filtering, L2/3 neurons can be orientation selective. This is consistent with previous studies [2, 3]. Surprisingly, spatial clustering of similarly tuned neurons emerges in L2/3 when recurrent connections are broader than feedforward connections (alpha_R>alpha_F), which resembles the columnar maps of higher mammals, though weaker. We name this pattern ‘columnette’ (Fig. 1c).

This result could be intuitively interpreted in the spatial Fourier space: Both feedforward and recurrent input currents have low-pass structure in the Fourier domain, due to the spatial filtering of a Gaussian-shaped connectivity footprint. Their summation can be either low-pass when alpha_R< = alpha_F (Fig. 1d, left panel), or band-pass when alpha_R>alpha_F (Fig. 1d, right panel), which corresponds to a clustered pattern in the physical space.

Furthermore, we predict that the signal correlation between neurons decreases with distance (Fig. 1e). Especially, when alpha_R>alpha_F and ‘columnette’ emerges, the signal correlation shows non-monotonic dependence on distance.

Previous models of orientation maps typically use long-range lateral inhibition which gives rise to strong columnar periodicity [4]. In contrast, we show that in networks with spatially balanced excitatory and inhibitory connections, ‘columnette’, a weak columnar structure, can emerge without any feature based spatial organization of either feedforward inputs or recurrent coupling.

References

1.
Ringach DL, Mineault PJ, Tring E, et al. Spatial clustering of tuning in mouse primary visual cortex. Nature communications 2016, 7, 12270.
2.
Hansel D, van Vreeswijk C. The mechanism of orientation selectivity in primary visual cortex without a functional map. Journal of Neuroscience 2012, 32(12), 4049–4064.
3.
Pehlevan C, Sompolinsky H. Selectivity and sparseness in randomly connected balanced networks. PLoS One 2014, 9(2), e89994.
4.
Kaschube M, Schnabel M, Lowel S, et al. Universality in the evolution of orientation columns in the visual cortex. Science 2010, 330(6007), 1113–1116.

P127 Decoupled reaction times and choices in expectation-guided perceptual decisions

Lluís Hernández-Navarro¹, Ainhoa Hermoso-Mendizabal¹, Jaime de la Rocha², Alexandre Hyafil³

¹IDIBAPS, Barcelona, Spain; ²IDIBAPS, Theoretical Neurobiology, Barcelona, Spain; ³UPF, Center for Brain and Cognition, Barcelona, Spain

Correspondence: Lluís Hernández-Navarro (llhernandez@clinic.cat)

BMC Neuroscience 2019, 20(Suppl 1):P127

In perceptual categorization tasks, both reaction times (RTs) and choices not only depend on current stimulus information, but also on urgency and prior expectations. To study them, we trained 10 rats in a two-alternative forced choice auditory discrimination task in free-response paradigm. The standard Drift Diffusion Model (DDM) for evidence accumulation up-to-threshold predicts a modulation of RTs by evidence strength. However, rats showed stimulus-independent RTs for fast, ‘express’ responses (RT<80ms,≈35% of trials). On the other hand, rats’ express choices were clearly modulated by stimuli because their express performance was significantly above chance (also for unbiased trials), and increased with RT. Additionally, in≈20% of trials, rats aborted fixation close to the onset of the stimulus, i.e. fixation break (FB, unrewarded).

The stimulus-independent express RTs, FBs and the increase of performance with RT for unbiased trials are inconsistent with standard DDMs for decision-making. Therefore, we propose a novel variant in which rats’ responses are triggered by independently integrating time and evidence. In this Dual DDM (2DM), time is tracked by a single-threshold DDM with constant bound initiating before the stimulus onset. This time integrator acts as both, an anticipation signal and an urgency signal. The evidence integrator is a standard DDM (two-threshold, constant-bound) that starts integrating sensory evidence some sensory delay after stimulus onset. The response of the rat is triggered when a bound is reached (either time-bound or evidence-bound). The choice of the rat is always set by the accumulated evidence at response time. The unconstrained fit of the 2DM to the full RT distributions provides initial, strong and consistent evidence across rats for the dual nature of their decision process.

We also introduced correlations in the stimulus sequence to induce trial-dependent expectations to repeat or alternate the previous response. We first found that, surprisingly, post-error slowing arose from two distinct phenomena: a slowing of the time integrator, and a lower stimulus sensitivity (i.e. slower integration to threshold) of the evidence integrator. Also, as expected, the evidence integrator was strongly influenced by history biases. We were able to decouple the contribution of the ‘lateral bias’ (i.e. accumulated ‘win-stay’ side bias) and the ‘transition bias’ (i.e. accumulated bias to repeat or alternate the previous response) on rats’ decisions. By maximum likelihood fitting (with L2 regularization) of the 2DM to rats’ choices, we consistently found that the lateral bias arises as a constant bias in the drift of the evidence integrator, whereas the transition bias is implemented as an initial offset of the evidence integrator.

We also found an unexpected modulation of the time integrator with history biases: it was slower under an expectation to repeat, while it became faster under an expectation to alternate. Preliminary results seem to support a distinct impact of the lateral and the transition bias also on the time integrator.

In conclusion, current standard models of decision making predict a direct relation between evidence accumulation and RTs, which is inconsistent with experimental observations in rats. A novel dual model, grounded on an independent integration of time and evidence, is able to capture rat’s behavior, and even decouple the impact of distinct history biases on RTs and choices.

P128 V1 visual neurons: receptive field types vs spike shapes

Syeda Zehra¹, Hamish Meffin², Damien Hicks³, Tatiana Kameneva¹, Michael Ibbotson⁴

¹Swinburne University of Technology, Telecommunication Electrical Robotics and Biomedical Engineering, Melbourne, Australia; ²University of Melbourne, Department of Optometry and Visual Science, Melbourne, Australia; ³Swinburne University, Department of Physics and Astronomy, Hawthorn, Australia; ⁴National Vision Research Institute, University of Melbourne, Melbourne, Australia

Correspondence: Tatiana Kameneva (tkameneva@swin.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P128

People with retinitis pigmentosa (RP) and age-related macular degeneration (AMD) lose retinal cells called photoreceptors that convert light energy into electro-chemical signals. However, many other types of retinal neurons survive in RP and AMD. It is possible to return a rudimentary vision to people with these diseases by stimulating remaining neurons in the retina with small electrical currents via an implanted electrode array. To improve efficacy of visual prostheses it is important to understand electrophysiology of different classes of visual neurons.

We used machine learning techniques to divide previously recorded data into clusters. We analyzed if the clusters discovered using the machine learning technique corresponded to the cell receptive field classifications. Extracellular recordings with 32 electrode array were collected from 189 V1 cortical neurons in anaesthetised cats. For each cell, a spike with the largest amplitude (out of 32 recordings) was analysed. White noise light stimulation protocol was implemented to classify receptive field size for each cell. Recorded extracellular spikes were spike sorted and used for clustering analysis. Wavelet decomposition was used to decompose experimentally recorded data into coefficients at five levels (the number of levels was based on the number of samples in the data). The coefficients at levels 3, 4 and 5 were used as input into K-means algorithm to classify data into clusters. The number of clusters in the algorithm was chosen to match six receptive field types.

Results show that clusters found by wavelet decomposition have some overlap with the receptive field types, i.e. cells with the same receptive field types have similar shapes of extracellular spikes. The clusters can be divided into triphasic slow, triphasic fast, double spikes, upwards, biphasic and fast spikes. In addition, the extracellular spikes were clustered into fast and slow groups which corresponded to previously published results for cortical visual neurons.

Understanding the differences in electrophysiological properties between V1 neurons is important for the advancement of basic neuroscience. In addition, our results may have an important implication on the development of stimulation strategies for visual prostheses.

P129 Synaptic basis for contrast-dependent shifts in functional cell identity in mouse primary visual cortex

Molis Yunzab¹, Veronica Choi², Hamish Meffin¹, Shaun Cloherty³, Nicholas Priebe², Michael Ibbotson¹

¹National Vision Research Institute, Melbourne, Australia; ²University of Texas Austin, Centre for Learning and Memory, Austin, United States of America; ³Monash University, Department of Physiology, Clayton, Australia

Correspondence: Molis Yunzab (molisyunzab@me.com)

BMC Neuroscience 2019, 20(Suppl 1):P129

Neurons in the mammalian primary visual cortex (V1) are classically labelled as either simple or complex based on their response linearity. A fundamental transformation that occurs in the mammalian visual cortex is the change from linear, polarity-sensitive responses of simple cells to nonlinear, polarity-insensitive responses of complex cells. While the difference between simple and complex responses is clear when the stimulus strength is high, reducing stimulus strength (e.g. contrast) diminishes the differences between the two cell types and causes some complex cells to respond as simple cells. This contrast-dependent transformation has been observed in extracellularly recorded spiking responses in V1 of mouse, cat and monkey. However, the mechanism underlying the phenomenon is unclear. In this study, we first explored two models that could potentially explain the contrast-dependent transformation and then examined the signature of the potential models by recording both the spiking and subthreshold responses of mouse V1 neurons using in vivo whole cell recordings. In the first candidate model the contrast-dependent shifts in complex cell responses emerge due to the “iceberg” effect, generated by the biophysical spike threshold, in which not all synaptic responses are converted into spikes at low contrast. However, we found systematic shifts in the degree of complex cell responses in mouse V1 at the subthreshold level, demonstrating that synaptic inputs change in concert with the shifts in response linearity and that this change cannot be explained with a simple threshold nonlinearity model. In the second candidate model recurrent amplification of the network acts as a critical component in generating linear or nonlinear responses in complex cells when input gain is low or high, respectively [1]. This model predicts that both spiking and subthreshold responses undergo contrast-dependent shifts in response linearity. Our experimental data confirms that this is the case in mouse V1 neurons. In conclusion, while the threshold nonlinearity may play an additional role in altering the response linearity of neurons [2], there is a clear synaptic component to the shift in response linearity that is likely driven by the changing recurrent inputs received from the cortical network.

References

1.
Chance FS, Nelson SB, Abbott LF. Complex cells as cortically amplified simple cells. Nature Neuroscience 1999, 2, 277–282.
2.
Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of threshold to the dichotomy of cortical simple and complex cells. Nature Neuroscience 2004, 7, 1113–1122.

P130 An encoding mechanism for translating between temporal sequences and spatial patterns

Nathalia Cristimann¹, Gustavo Soroka², Marco Idiart¹

¹Universidade Federal do Rio Grande do Sul, Institute of Physics, Porto Alegre, Brazil; ²Universidade Federal do Rio Grande do Sul, Instituto de Ciências Básicas da Saúde, Porto Alegre, Brazil

Correspondence: Nathalia Cristimann (nmcristimann@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P130

There are evidences that different brain networks may have distinct forms of holding information, both in terms of mechanism and coding. In particular, when modeling memory function in the brain, two theoretical frameworks have been used: recurrent attractor networks and bistability based working memory buffers. Recurrent attractor networks store information in the synaptic connections, and memory is a network property. On the other hand, working memory buffers may rely on short-lived changes, sometimes at single cell level, and have a much lower storage capacity that can be circumvent, for instance, by a multiplexing code like the theta-gamma temporal code. Moreover, while it is likely that recurrent networks could present an irregular asynchronous state the same may not be true of the working memory buffers of the theta-gamma kind where synchrony is an essential feature. But ultimately if both networks are to be present in the brain they need to communicate to exchange information. In this work we propose a mechanism using inhibitory competition that provides a satisfactory functional coupling between such different forms of information storage and processing. We focus in the simpler case of a neural architecture comprised of two working memory buffers that interact via a recurrent neural network (RNN) that is capable of holding long term memories as attractors. In the network the temporal sequence coming from the input buffer is stored as a spatial pattern in the RNN, and subsequently decoded as a temporal pattern in the output buffer. We investigate its encoding and decoding capabilities in presence of noise and incomplete information. We also address the question of whether a random network structure in RNN could be sufficient to guarantee information transfer between the two buffers. We explore 4 models of random connectivity: Erdos-Renyi (ER), Watts-Strogatz (WS), Newmann-Watts-Strogatz (NWS) and Barabasi-Albert (BA). Using as a metric for the encoding/decoding error the edit distance between the output and input sequences, we show that the WS and NWS models, which correspond to networks that have small-world properties, are more efficient than the other models. When compared to the ER model, the WS and NWS models present a smaller error for almost every value of the connectivity parameters.

P131 Building Python interactive neuroscience applications using Geppetto

Matteo Cantarelli^1,2, Padraig Gleeson⁵, Adrian Quintana^1,3, Angus Silver⁵, William W Lytton⁶, Salvador Dura-Bernal⁶, Facundo Rodriguez¹, Bóris Marin^7,5, Robert Court⁴, Matt Earnshaw⁵, Giovanni Idili^1,2

¹MetaCell Ltd. LLC, Oxford, UK/Boston, USA; ²OpenWorm Foundation, Delaware, USA; ³EyeSeeTea Ltd., London, UK; ⁴Institute for Adaptive and Neural Computation, University of Edinburgh, UK; ⁵University College London, Dept. of Neuroscience, Physiology & Pharmacology, London, United Kingdom; ⁶State University of New York Downstate Medical Center, Brooklyn, NY, USA; ⁷Universidade Federal do ABC, São Bernardo do Campo, Brazil

Correspondence: Matteo Cantarelli (matteo@metacell.us)

BMC Neuroscience 2019, 20(Suppl 1):P131

Geppetto [1] is an open-source platform for building web applications for visualizing neuroscience models and data, as well as managing simulations. Geppetto underpins a number of neuroscience applications available to the research community, including Open Source Brain (OSB) [2], Virtual Fly Brain (VFB) [3], NetPyNE-UI [4] and HNN-UI [5]. While Geppetto traditionally employed a Java backend we have now augmented it to also support Python. This means that applications built with Geppetto now also offer their users the ability to interact directly with any underlying Python APIs, while seamlessly keeping the user interface synchronized. To make this possible we developed a series of Javascript-Python Connectors that let developers easily build a user interface, whose state can be controlled from a Python model and vice versa. Neuroscience applications built with Python Geppetto have the advantage of bridging the beginner/advanced user usability gap. Beginner users will be able to interact with a user interface that will simplify the accessibility of the underlying APIs. Expert users will be able from the same GUI to programmatically interact with the underlying data models and Python APIs while the user interface will be kept updated graphically reflecting any programmatic changes. Python Geppetto applications can be deployed locally, installed using standard Python packages (accessible from PyPI) or Docker and deployed remotely on the web using Kubernetes and Jupyter Hub.

References

1.
Cantarelli M, et al. Geppetto: a reusable modular open platform for exploring neuroscience data and models. Philosophical Transactions of the Royal Society B: Biological Sciences 2018 Sep 10;373(1758):20170380.
2.
Gleeson P, et al. Open Source Brain: a collaborative resource for visualizing, analyzing, simulating and developing standardized models of neurons and circuits. bioRxiv 2018 Jan 1:229484. (https://doi.org/10.1101/229484)
3.
Armstrong JD, et al. Towards a virtual fly brain. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2009 Jun 13;367(1896):2387–97. (https://doi.org/10.1098/rsta.2008.0308)
4.
Dura-Bernal S, et al. NetPyNE: a tool for data-driven multiscale modeling of brain circuits. bioRxiv 461137(2018) [Preprint]; (Under review in eLife)
5.
Neymotin S, et al. Human Neocortical Neurosolver. 2018. https://doi.org/10.5281/zenodo.1446517

P132 Hierarchy of inhibitory circuit acts as a switch key for network function in a model of the primary motor cortex

Heidarinejad Morteza¹, Zhe Sun¹, Jun Igarashi¹

¹Riken, Computational Engineering Applications Unit, Saitama, Japan

Correspondence: Heidarinejad Morteza (s.heidarinejadmohamm@riken.jp)

BMC Neuroscience 2019, 20(Suppl 1):P132

The primary motor cortex (M1) is the core region for body action and movements. Here we have been constructed a large-scale real spiking neural network of M1, based on anatomical and electrophysiological data [1, 2]. The model includes 5 layers L1, L23, L5A, L5B, and L6 and 19 different cell types. Spatial extents and connection probabilities among the neurons were estimated from experimental Laser Scanning Photo Stimulation (LSPS) data and unitary synaptic connections.

First, the virtual LSPS experiment was conducted. Those already reported by experiments [3], repeated by our results, while other non-reported maps were reported by our stimulation.

Also, we conducted columnar shape stimulation to inhibitory neurons. To elucidate the application of such a structure, we assumed a vertical cylinder and applied the stimulation on neurons inside. All neurons of 5 populations of L1-ENGC, L1-SBC, L2/3-PV, L2/3-SST, and L2/3-VIP were stimulated and spiking activity of all neurons was recorded.

As a result, SBC, PV, and SST interneurons were categorized as local inhibitors. Projection of all these 3 interneurons were confined to the inside of assumed column. In contrast, stimulation of layer 1 ENGC and layer 2/3 VIP interneurons showed both vertical and horizontal propagation. ENGC cells almost inhibited all neurons of layer 1 and 2/3, plus SST neurons of all layers and VIP interneurons activated all neuron types including PV neurons in all layers (excluding layer 1) except SST neurons which are inhibited by VIPs.

Inhibition of inhibition is a well-known logic to control the activity of cortex. ENGCs and SBCs in layer 1 and SSTs of layer 2/3 inhibit VIP neurons, while VIP interneurons themselves have a versatile impact on others. The results suggest that VIP neurons may act as a switch for activation of inhibition on entire cortical network.

References

1.
Fino E, Yuste R. Dense inhibitory connectivity in neocortex. Neuron 2011 Mar 24;69(6):1188–203.
2.
Jiang X, Shen S, Cadwell CR, et al. Principles of connectivity among morphologically defined cell types in adult neocortex. Science 2015 Nov 27;350(6264):aac9462.
3.
Hooks BM, Hires SA, Zhang YX, et al. Laminar analysis of excitatory local circuits in vibrissal motor and sensory cortical areas. PLoS Biology 2011 Jan 4;9(1):e1000572.

P133 Spatially organized connectivity for signal processing in a model of the rodent primary somatosensory cortex

Zhe Sun¹, Heidarinejad Morteza¹, Jun Igarashi¹

¹Riken, Computational Engineering Applications Unit, Saitama, Japan

Correspondence: Zhe Sun (zhe.sun.vk@riken.jp)

BMC Neuroscience 2019, 20(Suppl 1):P133

Understanding the structure and function of S1 is critical for figuring out the information process mechanism in the sensory nervous system. Spatial organization of connections, layers, and columns in the somatosensory cortex is considered to work as information processing device for integration of inputs and selection of outputs. However, it remains unknown how different types of connections with different spatial extent work for sensory processing in the primary somatosensory cortex (S1). To investigate it, we developed a three-dimensional model of spiking neural network model of the S1 based on anatomical and electrophysiological experiment results [1, 2]. The S1 model comprised 7 layers, with 1 excitatory neuron and 5 inhibitory neuron types (L1: 2 inhibitory neuron types; L2 and L3: 3 inhibitory and 1 excitatory neuron types; L4, L5A, L5B&L6: 2 inhibitory and 1 excitatory neuron types). We used the layer thicknesses and the cell densities of the mouse’s S1 data. Leaky integrate-and-fire neuron model was used for all neuron types. We used the information of spatial extents, probabilities, and connectivity from the reports of laser-scanning photo-stimulation (LSPS) experiments and patch clamp recordings. We used Gaussian function as the connection probability function. All simulations were performed using pyNEST 2.16 on HOKUSAI supercomputer in RIKEN. The simulation time step was set to 0.1 ms. When we performed a size of 1 mm² S1 simulation on one compute node with 40 CPU cores, it took 6 minutes to construct the network. And it also took 0.5 minute to complete the simulation of 1 second of neuronal network activity in real biological time. Total neuron number in the 1mm² microcircuit is 94396.By adjusting external Poisson input for each kind of neuron, we realized resting state firing rate for all neuron types in our S1 model. We made a virtual slice of the S1 whose shape was a cube of 1600 × 400 × 1400 micron. We first performed virtual LSPS experiments for excitatory and inhibitory connections to all neuron types. The responses of neurons to LSPS were qualitatively similar to those in real LSPS experiments. Most importantly, to investigate the relation between excitatory and inhibitory signals, we compared the excitatory and inhibitory conductance with changing distances between neurons with external stimulation and recorded neurons. The excitatory and inhibitory synaptic conductance of L2/3 and L5 excitatory neurons similarly decayed with increasing in the horizontal distance between stimulation sites and positions of recorded neurons, which is similar to real experimental results [3]. These results suggest that spatial extents of different connections may cause spatially coupled excitation and inhibition in L2/3 and L5A, which may lead to cooperative information processing by excitation and inhibition.

Acknowledgement: This work was supported by the Ministry of Education, Culture, Sports, Science and Technology(MEXT) as ”Exploratory Challenge 4 on Post-K Computer”.

References

1.
Kätzel D, Zemelman BV, Buetfering C, Wölfel M, Miesenböck G. The columnar and laminar organization of inhibitory connections to neocortical excitatory cells. Nature Neuroscience 2011 Jan;14(1):100.
2.
Hooks BM, Hires SA, Zhang YX, et al. Laminar analysis of excitatory local circuits in vibrissal motor and sensory cortical areas. PLoS Biology 2011 Jan 4;9(1):e1000572.
3.
Adesnik H, Scanziani M. Lateral competition for cortical space by layer-specific horizontal circuits. Nature 2010 Apr;464(7292):1155.

P134 Probing the association between axonal sprouting and seizure activity using a coupled neural mass model

Jaymar Soriano¹, Takatomi Kubo², Kazushi Ikeda²

¹University of the Philippines, Department of Computer Science, Quezon City, Philippines; ²Nara Institute of Science and Technology, Ikoma, Japan

Correspondence: Jaymar Soriano (jbsoriano@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P134

Initiation of seizure activity in the brain is generally believed to be caused by an alteration in excitation-inhibition balance such as when dendritic inhibition is impaired. Alternatively, it is also believed that seizure activity can arise due to a synaptic reorganization of neural networks such as the emergence of axonal sprouting in which axonal processes of a neuron grow out and create synaptic connections with the dendritic processes of other neurons. In fact, co-occurrence of seizure activity and axonal sprouting has been established in epilepsy and lesion models. For example, Cavazos et al. [1] report that alterations in terminal projections of mossy fiber pathway progressed with the evolution of kindled seizures. It remains unclear, however, whether axonal sprouting is a cause or effect of seizure activity or how and when it contributes to brain dysfunction and initiation of seizure activity. In this study, we used a coupled neural mass model to demonstrate that epileptic discharge activity can initiate from non-pathologic brain regions, reciprocally coupled to simulate an emergence of axonal sprouting. As axonal sprouting progresses and creates stronger connections between the brain regions, the discharge activity transitions into different types of seizure activity such as high frequency discharges, periodic oscillations, and low-amplitude high-frequency rhythms; increasing in beta-activity component (Fig. 1). These transitions can also be brought by an increase in post-synaptic gain, possibly concurrent with an increase in number of synaptic connections. Such increase in post-synaptic gain captures observed aberrant post-synaptic morphologies like the formation of multiple spine buttons similar to those observed with long term potentiation. The results delve into the possibility that axon sprouting maybe a primary mechanism, possibly concomitant with impaired inhibition, which can provide insights on how networks of brain regions are recruited and give rise to the generalization of seizure activity. In the future, we aim to construct a generative model for seizure activity initiation and propagation for diagnosis and treatment of patients with primary or secondary generalized epilepsy [2].

References

1.
Cavazos JE, Golarai G, Sutula TP. Mossy fiber synaptic reorganization induced by kindling: time course of development, progression, and permanence. Journal of Neuroscience 1991 Sep 1;11(9):2795–803.
2.
Proix T, Bartolomei F, Guye M, Jirsa VK. Individual brain structure and modelling predict seizure propagation. Brain 2017. 140(3), 641–654.

P135 Evaluation of signal processing of Golgi cells and Basket cells in vestibular ocular reflex motor learning using artificial cerebellum

Taiga Matsuda, Keiichiro Inagaki

Chubu University, Kasugai, Japan

Correspondence: Taiga Matsuda (tr18016-4399@sti.chubu.ac.jp)

BMC Neuroscience 2019, 20(Suppl 1):P135

The vestibuloocular reflex (VOR) is one of the most popular model systems to study motor learning due to its clear function (stabilization of our vision) and ease in recording its input (head rotation) and output (eye movement) signals. The motor learning of the VOR requires the cerebellar flocculus. The flocculus receives sensory and motor information through mossy and climbing fibers, and outputs motor related activities to vestibular nuclei via Purkinje cell axons. Between these inputs and outputs lies a rich network of interneurons, most of them inhibitory (GABAergic). While most of the previous studies on VOR motor learning have focused on responses of Purkinje cells, little attention has paid to roles of cerebellar inhibitory interneurons due to a difficulty in identifying and recording those neurons in cerebellar cortex in behaving animals. Herein, we have constructed a computational model of the VOR that explicitly implements the anatomically realistic floccular neuronal network structure so that activities of each inhibitory interneuron can be evaluated. The model also allows us to knocked-out any specific interneuron(s) at any timing of VOR motor learning. The model consists of 20 Purkinje, 10000 granular, 900 Golgi, and 60 basket/stellate cells each of which is described as a conductance based spiking neuron model. These neuron models are connected, preserving convergence/divergence ratios between neuron types [1]. As bases of VOR motor learning, climbing fiber spike timing dependent LTD and LTP have been implemented at parallel fiber—Purkinje cell synapses. To induce VOR motor learning we simulated continuous application of visual-vestibular mismatch paradigm: VOR enhancement (VORe) and VOR suppression. In the VORe, the head and visual stimulus was applied out of phase, while those are given in phase in the VORs. Continuous application of VORe and VORs stimulus, VOR gain measured in darkness without visual stimulation increases or decreases, respectively. Furthermore, knock-out of Golgi and/or basket/stellate cells is simulated to investigate roles of those cells in the VOR motor learning.

We confirmed that the model reproduces adaptive changes of VOR gain with/without Golgi cells or basket/stellate cells. When the Golgi cell knocked-out in the motor learning, increase of VOR gain was slightly impaired while its decrease was enhanced. When the basket/stellate cell knocked-out, decrease of VOR gain was slightly impaired, while its increase was enhanced. Interestingly, retention of acquired VOR performance was affected for only low gain condition by elimination of Golgi cell or Basket/Stellate cell after the VOR motor learning. Those results indicated that the inhibitory interneurons play key roles in the high and low gain VOR motor learning, and retention of those memories.

Acknowledgement: A part of this work supported by JSPS KAKENHI Grant Number 17K12781 (KI)

Reference

1.
Inagaki K, Hirata K. Computational theory underlying acute vestibulo-ocular reflex motor learning with cerebellar long-term depression and long-term potentiation. The cerebellum 2017, vol.16, pp.827–839.

P136 Development of a self-motivated treadmill task that quantifies differences in learning behavior in mice for optogenetic studies of basal ganglia

Po-Han Chen, Dieter Jaeger

Emory University, Department of Biology, Atlanta, GA, United States of America

Correspondence: Po-Han Chen (chenabe97@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P136

The basal ganglia (BG) is involved in various cognitive functions, including stimulus-response associative learning and decision making. The two major pathways that connect the striatum and the output nuclei of the basal ganglia are direct and indirect, with the substantia nigra pars reticulata (SNr) / globus pallidus internus (GPi) inhibitory projections providing the final output. Signals through these pathways converge to inhibit the glutamatergic thalamic nuclei, which output onto the cortex. GPi activity suppresses inappropriate motor activity that may conflict with the movement being performed, making it an important integrator of learned reward-related behaviors [3]. Recent innovations in genetic technology resulted in the ability to stimulate distinct neural populations with light through the insertion of light sensitive ion channels. Optogenetic manipulations to the basal ganglia has shown to alter behavioral execution in mice, but what exactly are these behaviors that are being altered and to what degree? In our studies we have designed a self-paced treadmill task that will help better our understanding of how movement planning intersects with a self-motivational task. Ultimately, the goal is to use this task with optogenetic methods to activate GPi and determine how it reduces learned reward-seeking behaviors.

We designed an open field environment with a horizontal treadmill and a simple water delivery system. Mice are water-restricted to increase motivation. During training, once the mouse runs above a 200 cm distance threshold on the treadmill, an associated visual light cue signals that the water reward is ready. Water delivery is triggered by the breaking of an IR bream at the spout. To investigate the motivation aspect, we manipulate the reward sizes, which become a function of the run distance in a set period (15-60 s) and are delivered at the end of each period. Higher motivation is signaled by higher run speeds or run distances, as well as by between-trial response time. With this task, the effect of GPi activation on learned behavior and motivation can be elucidated with expression of Channelrhodopsin (ChR2) through AAV injection in GPi. A glass fiber will be implanted to allow for light stimulation of GPi. Optogenetic stimulation of GPi will be delivered at various intervals, such as right before cue delivery or during the behavioral response, to observe the effect of BG control has on learned behavior at different parts of execution. Because GPi provides inhibitory input to motor planning circuits in the cortex, we expect a reduction in learned behavior across all levels of baseline motivation. Future investigation of BG circuits and their movement effects can also use this task for examination into reward-seeking behavior and self-motivation.

References

1.
Albin RL, Young AB, Penney JB. The functional anatomy of basal ganglia disorders. Trends in Neurosciences 1989; 12:366–375.
2.
DeLong MR. Primate models of movement disorders of basal ganglia origin. Trends in Neurosciences 1990; 13:281–285.
3.
Turner RS, Desmurget M. Basal Ganglia Contributions to Motor Control: A Vigorous Tutor. Current Opinions Neurobiology 2010; 20(6): 704–716.
4.
Aravanis AM, Wang LP, Zhang F, et al. An optical neural interface: in vivo control of rodent motor cortex with integrated fibreoptic and optogenetic technology. Journal of Neural Engineering 2007; 4:143–156.
5.
Sanders TH, Jaeger D. Optogenetic stimulation of cortico-subthalamic projections is sufficient to ameliorate bradykinesia in 6-ohda lesioned mice. Neurobiology of Disease 2016; 95:225–237.

P137 Compensatory effects of dendritic retraction on excitability and induction of synaptic plasticity

Martin Mittag¹, Manfred Kaps², Thomas Deller³, Hermann Cuntz⁴, Peter Jedlicka⁵

¹Justus Liebig University Giessen, Giessen, Germany; ²Justus Liebig University Giessen, Department of Neurology, Giessen, Germany; ³Goethe University Frankfurt, Institute of Clinical Neuroanatomy, Neuroscience Center, Frankfurt am Main, Germany; ⁴Frankfurt Institute for Advanced Studies (FIAS) & Ernst Strüngmann Institute (ESI), Computational Neuroanatomy, Frankfurt/Main, Germany; ⁵Justus Liebig University, Faculty of Medicine, Giessen, Germany

Correspondence: Martin Mittag (martin.mittag@gmx.de)

BMC Neuroscience 2019, 20(Suppl 1):P137

How can a neuron maintain its function under changed physiological or pathological conditions? Brain lesions affect not only the locally damaged area but have an impact also on postsynaptic regions. Lesion-induced denervation of connections from the entorhinal cortex causes significant loss of synapses in the hippocampal dentate gyrus. Subsequently, dendritic retraction occurs in the postsynaptic target area containing hippocampal dentate granule cells. Our previous models showed that dendritic retraction is capable of increasing the excitability of neurons thus compensating for the denervation-evoked loss of synapses. The firing rate remains similar in healthy and denervated neurons despite weaker synaptic input upon denervation (firing rate homeostasis). However, this effect was computed only for stochastically stimulated AMPA synapses [1] but not for more realistic AMPA/NMDA synapses. Furthermore, a boost in backpropagating action potentials (bAPs) in denervated granule cells might affect homeostasis of synaptic plasticity. Therefore, here we investigated the consequences of dendritic retraction for (1) firing rate homeostasis and (2) NMDA receptor-dependentsynaptic plasticity in biologically realistic compartmental models driven by AMPA/NMDA synapses. Our simulations predict that dendritic retraction supports firing rate homeostasis and partially also synaptic plasticity homeostasis.

Acknowledgement: The work was supported by BMBF (No. 01GQ1406 – Bernstein Award 2013 to H.C.), University Medical Center Giessen and Marburg (UKGM; to P.J. and M.K.), LOEWE CePTER – Center for Personalized Translational Epilepsy Research (to P.J. and T.D.)

Reference

1.
Platschek S, Cuntz H, Vuksic M, Deller T, Jedlicka P. A general homeostatic principle following lesion induced dendritic remodeling, Acta Neuropathologica Communications 2016

P138 Lognormal distribution of spine sizes is preserved following homo- and heterosynaptic plasticity in the dentate gyrus

Nina Rößler¹, Tassilo Jungenitz², Stephan Schwarzacher², Peter Jedlicka³

¹Goethe University Frankfurt, Frankfurt, Germany; ²Goethe University Frankfurt, Institute of Clinical Neuroanatomy, Frankfurt, Germany; ³Justus Liebig University, Faculty of Medicine, Giessen, Germany

Correspondence: Nina Rößler (nina.roessler@gmx.net)

BMC Neuroscience 2019, 20(Suppl 1):P138

The dentate gyrus is one of two brain regions that exhibit adult neurogenesis. It was shown to be important for hippocampal learning and memory processes, which are based on synaptic plasticity. We have recently reported structural homo- and heterosynaptic long-term synaptic plasticity emerging in adult-born dentate granule cells at a cell age of 35 days [1]. High frequency stimulation of the medial perforant path in this and later stages of adult neurogenesis led to spine enlargement in stimulated dendritic regions (homosynaptic structural LTP) and a concurrent spine shrinkage in neighboring non stimulated dendritic segments (heterosynaptic structural LTD).

Here we perform a follow-up systematic analysis of spine plasticity data. Our results show that spine sizes follow a lognormal distribution, both in dendritic segments undergoing homosynaptic spine enlargement as well as heterosynaptic spine shrinkage, suggesting that the overall distribution of spine sizes does not change. We are currently developing computational models, which should account for the observed spine changes in adult-born granule cells and provide new insights into plasticity rules in the dentate gyrus.

Reference

1.
Jungenitz T, et al. Structural homo- and heterosynaptic plasticity in mature and adult newborn rat hippocampal granule cells. PNAS 2018, 115(20):e4670e–4679.

P139 Inferring the dynamic of personalized large-scale brain network models using Bayesian framework

Meysam Hashemi¹, Anirudh Vattikonda¹, Viktor Sip¹, Maxime Guye², Marmaduke Woodman¹, Viktor Jirsa¹

¹Aix-Marseille Université, Institut de Neurosciences des Systèmes, Marseille, France; ²Aix-Marseille Université, Institut de Neurosciences de la Timone, Marseille, France

Correspondence: Meysam Hashemi (meysam.hashemi@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):P139

Despite the importance and common use of Bayesian inference in brain network modelling to understand how experimental modalities result from the dynamics of coupled neural populations, many challenges remain to be addressed in this context. The recent successful personalized strategies towards epilepsy treatment [1] motivated us to focus on Bayesian parameter estimation of Virtual Epileptic Patient (VEP) brain model. The VEP is based on personalized brain network models derived from non-invasive structural data of individual patients. Using VEP as generative model, and the recently developed Bayesian algorithms implemented in probabilistic programming languages [2], our aim is to infer the dynamics of brain network model from the patient’s empirical data. We estimate the spatial dependence of excitability and provide a heat map capturing an estimate of epileptogenicity and our confidence thereof. The Bayesian framework taken in this work proposes an appropriate patient-specific strategy to infer epileptogenicity of the brain regions to improve outcomes after epilepsy surgery.

References

1.
Jirsa VK, Proix T, Perdikis D, et al. The virtual epileptic patient: individualized whole-brain models of epilepsy spread. Neuroimage 2017 Jan 15;145:377–88.
2.
The Stan Development Team. Stan: A C ++ Library for Probability and Sampling, 2015.

P140 Personalized brain network model for deep brain stimulation on treatment-resistant depression: Spatiotemporal network organization by stimulation

Sora An¹, Jan Fousek¹, Vineet Tiruvadi², Filomeno Cortese³, Gwen van der Wijk⁴, Laina McAusland⁵, Rajamannar Ramasubbu⁶, Zelma Kiss⁷, Andrea Protzner⁸, Viktor Jirsa¹

¹Aix Marseille Universite, Institute de Neurosciences, Marseille, France; ²Emory University School of Medicine, Department of Psychiatry and Behavioral Sciences, Atlanta, Georgia, United States of America; ³University of Calgary, Seaman Family MR Centre, Foothills Medical Centre, Hotchkiss Brain Institute, Calgary, Alberta, Canada; ⁴University of Calgary, Department of Psychology, Calgary, Alberta, Canada; ⁵University of Calgary, Department of Clinical Neurosciences, Calgary, Alberta, Canada; ⁶University of Calgary, Hotchkiss Brain Institute, Cumming School of Medicine, Calgary, Alberta, Canada; ⁷University of Calgary, Hotchkiss Brain Institute, Department of Clinical Neurosciences, Calgary, Alberta, Canada; ⁸University of Calgary, Hotchkiss Brain Institute, Department of Psychology, Calgary, Alberta, Canada

Correspondence: Sora An (an.sora@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):P140

Deep brain stimulation (DBS) is a surgical technology in which fine electrodes are implanted into the brain and connected to a type of pacemaker. This applies chronic high frequency electrical stimulation to the brain 24 hours a day for years. It has revolutionized the treatment of movement disorders, such as Parkinson disease, and is being studied as potential treatment for several other disorders, including treatment resistant depression (TRD). In TRD, the subcallosal cingulate gyrus (SCG) is most commonly used as a DBS target because it shows hyperactivity in patients with depression, normalization of activity in the context of positive response to other antidepressant treatments, and because the SCG has structural connections with several key regions involved in mood regulation.DBS treatment outcome has been variable, with some studies failing to find effects, and others finding positive outcomes in up to 80% of patients. Potential reasons for these inconsistent findings are that the ideal stimulation target location and ideal stimulation parameters are currently unknown. DBS for TRD is therefore still applied on a trial-and-error basis, which, especially considering the invasive nature of this treatment, is far from ideal. Determining the exact stimulation conditions that generate good treatment outcome is thus crucial for applying DBS to TRD.

In this study, we propose a computational modeling approach for identifying the ideal stimulation location. Toward this end, we have built personalized brain network models based on neuroimaging data obtained from each patient, using The Virtual Brain (TVB) platform. Then, spatiotemporal brain activation patterns following the stimulation are simulated. In the simulations, electrical stimulation is systematically applied to each electrode contact (8 contacts per patient), and the fiber tracts activated in each case are determined from the voltage distribution across each fiber tract. The voltage distribution is calculated based on patient-specific contact positions and anatomical locations of fiber tracts, by employing the finite difference method. Source activity from each brain node is projected to 65-channel electroencephalography (EEG) sensor space, through the forward solution. In order to verify the validity of the proposed model, the simulated EEG signals are compared with empirical data, i.e., the event-related potentials recorded by means of EEG from the individual patient. The results show that brain network models based on fiber tract activation are able to reproduce the spatiotemporal response patterns according to the stimulation location, which can be useful to optimize the active contact positions in individual patients. This study sets the stage forapplying computational modeling in the context of personalized medicine, where an in-silico brain platform allows clinicians to test andoptimize DBS strategies for individual patients, prior to implantation.

Acknowledgements: We wish to acknowledge the financial support of the following agencies; Fondation pour la Recherche Médicale (FRM) (grant number DIC20161236442), European Commission’s Human Brain Project (grant agreement H2020-720270), the SATT Sud-Est (TVB-Epilepsy) to VJ; Alberta Innovates Health Solutions (previously, Alberta Heritage Foundation for Medical Research) to ZK and RR; Natural Sciences and Engineering Council of Canada (NSERC; grant number 418454-2013) to ABP.

P141 Transmission time delays organize the brain network synchronization dynamics

Spase Petkoski, Viktor Jirsa

Aix-Marseille University, Institut de Neurosciences des Systèmes, Marseille, France

Correspondence: Spase Petkoski (spase.petkoski@univ-amu.fr)

BMC Neuroscience 2019, 20(Suppl 1):P141

Timings of the activity at brain regions, which can be described by their phases for oscillatory processes, are of crucial importance for the brain functioning. The structure of the brain constrains its dynamics through the delays due to propagation and the strengths of the white matter tracts [1]. Rhythms and their synchronization, as one of the key mechanisms of brain function [2] are particularly sensitive to delays, which become notably long in large-scale brain models with biologically realistic connectivity [3].

We show theoretical and in-silico numerical results for phase coherence between signals from different brain regions. For this we build on the Kuramoto model with spatially distributed time delays [4], where the network connectivity strengths and distances are defined by the connectome. Phase relations and their regions of stability are derived and numerically confirmed, showing that besides in-phase, clustered delays can induce anti-phase synchronization for certain frequencies, while the sign of the lags is determined by the inhomogeneous network interactions [5]. For in-phase synchronization faster oscillators always phase lead, while stronger connected nodes lag behind the weaker during frequency depression, which consistently arises for in-silico results (See Fig. 1). The statistics of the phases is calculated from the phase locking values, as in many empirical studies, and we scrutinize the method’s impact. The choice of surrogates does not affect the mean of the observed phase lags, but higher significance levels that are generated by some surrogates, cause decreased variance and might fail to detect the generally weaker coherence of the interhemispheric links. These links are also affected by the non-stationary and intermittent synchronization, which causes multimodal phase lags that can be misleading if averaged [5].

The architecture of the phase lags are confirmed for non-isochronous, nonlinearly damped, and chaotic oscillators, which show a robust switching from in to anti-phase synchronization by increasing the frequency, with a consistent lagging of the stronger connected regions [6]. Increased frequency and coupling are also shown to distort the oscillators by decreasing their amplitude, and stronger regions have lower, but more synchronized activity [6]. Taken together, the results indicate specific features in the phase relationships within the brain that need to hold for a wide range of local oscillatory dynamics, given that the time-delays of the connectome are proportional to the lengths of the structural pathways [5, 6].

References

1.
Sanz-Leon P et al. Mathematical framework for large-scale brain network modeling in the virtual brain. Neuroimage 2015, 111, 385–430
2.
Varela F, Lachaux J, Rodriguez E, Martinerie J. The brainweb: Phase synchronization and large-scale integration. Nature Review Neuroscience 2001, 2(4): 229–239
3.
Deco G, Jirsa V, McIntosh AR, Sporns O, Kötter R. Key role of coupling, delay, and noise in resting brain fluctuations. PNAS USA 2009, 106 (25): 10302–10307
4.
Petkoski S, et al. Heterogeneity of time delays determines synchronization of coupled oscillators. Physical Review E 2016, 94, 012209
5.
Petkoski S, et al. Phase-lags in large scale brain synchronization: Methodological considerations and in-silico analysis. PLoS Computational Biology 2018, 14(7), 1–30.
6.
Petkoski S, et al. Transmission time delays organize the brain network synchronization dynamics. Philosophical Transactions of the Royal Society A [in review]

P142 Mutual information vs. transfer entropy in spike-based neuroscience

Mireille Conrad, Renaud Jolivet

University of Geneva, Nuclear and Corpuscular Physics Department, Genève, Switzerland

Correspondence: Mireille Conrad (mireille.conrad@unige.ch)

BMC Neuroscience 2019, 20(Suppl 1):P142

Energetic constraints might limit and shape information processing in the brain, and it has been shown previously that synapses maximize energy efficiency of information transfer rather than information transfer itself. To investigate computation by neural systems, measuring the amount of information transferred between stimuli and neural responses is essential. Information theory offers a range of tools to calculate information flow in neural networks. Choosing the appropriate method is particularly important in experimental contexts, where technical limitations can complicate or limit the use of information theory.

Here, we will discuss the comparative advantages of two different metrics: mutual information and transfer entropy. We will compare their performance on biologically plausible spike trains and discuss their accuracy depending on various parameters, and on the amount of available data, a critical limiting factor in all practical applications of information theory. We will first demonstrate these metrics’ performances using synthetic random spike trains before moving on to more realistic spike-generating models. Those realistic models focus on the generation of input spike trains with a statistical structure similar to biological spike trains, and also on the generation of output spike trains with an experimentally-calibrated Hodgkin-Huxley-type model. We will conclude by discussing how these metrics can be used to study brain function, especially the effect of neuromodulators and learning rules as ways for synapses to maximize energy efficiency.

P143 Plasticity rules for learning sequential inputs under energetic constraints

Dmytro Grytskyy¹, Renaud Jolivet^1,2

¹University of Geneva, Geneva, Switzerland; ²CERN, DPNC, Genève, Switzerland

Correspondence: Dmytro Grytskyy (dmytro.grytskyy@etu.unige.ch)

BMC Neuroscience 2019, 20(Suppl 1):P143

Information measures are often used to assess the efficacy of neural networks and learning rules can be derived through optimization procedures on such measures [3, 8, 10]. There has also been recent interest for sequence learning for specific tasks [2], or with specific network configurations [7]. In biological neural networks, computation is restricted by the amount of available resources [4, 11]. Considering energy restrictions, it is reasonable to balance information processing efficacy with energy consumption [1]. Here, we obtain such an energy-constrained learning rule for inputs described as sequence of events.

We studied networks of non-linear Hawkes neurons and assessed information flow using mutual information. We then applied gradient descent for a combination of mutual information and energetic costs to obtain a learning rule. The rule obtained contains a sliding threshold similar to the Bienenstock-Cooper-Munro rule [5]. It contains terms local in time and in space, plus one global variable common to the whole network. The rule thus belongs to so-called three-factors rules, and the global variable could be related to neuromodulation [6]. Because that global variable integrates over time, consecutive inputs can influence synaptic changes triggered by preceding events. We additionally investigated the relation between that rule and STDP, and obtained different STDP-like learning windows for excitatory and inhibitory neurons.

Constraining energy consumption results in a rearrangement of the correspondence between inputs and respective outputs, with more frequent input patterns mapped to lower energy orbits. Taking into account unreliability of neural transmission results in an additional negative term in the learning rule proportional to the synaptic weight. This has the effect that extremely rare events aren’t learned, while moderately rare inputs evoke maximal network activity.

When different neurons respond to different inputs that are predictive of each other, synaptic weights between these neurons will be reinforced. Different inputs regularly occurring in close temporal relation to each other can be defined as a context, which can lead to the appearance of subnetworks coding for the whole context rather than for components of it, lowering energetic costs of that representation. For almost strict sequences, neurons representing late inputs in the sequence might be inhibited, reducing energy costs.

Acknowledgements: Supported by the Swiss National Science Foundation (31003A_170079) and by the Australian Research Council (DP180101494).

References

1.
Bourdoukan R, Barrett D, Deneve S, Machens CK. Learning optimal spike-based representations. In Advances in neural information processing systems 2012 (pp. 2285–2293).
2.
Brea J, Senn W, Pfister JP. Sequence learning with hidden units in spiking neural networks. In Advances in neural information processing systems 2011 (pp. 1422–1430).
3.
Chechik G. Spike-timing-dependent plasticity and relevant mutual information maximization. Neural Computation 2003 Jul 1;15(7):1481–510.
4.
Harris JJ, Jolivet R, Attwell D. Synaptic energy use and supply. Neuron. 2012 Sep 6;75(5):762–77.
5.
Intrator N, Cooper LN. Objective function formulation of the BCM theory of visual cortical plasticity: Statistical connections, stability conditions. Neural Networks 1992 Jan 1;5(1):3–17.
6.
Isomura T, Toyoizumi T. A local learning rule for independent component analysis. Scientific reports 2016 Jun 21;6:28073.
7.
Kappel D, Nessler B, Maass W. STDP installs in winner-take-all circuits an online approximation to hidden Markov model learning. PLoS Computational Biology 2014 Mar 27;10(3):e1003511.
8.
Linsker R. Local synaptic learning rules suffice to maximize mutual information in a linear network. Neural Computation 1992 Sep;4(5):691–702.
9.
Toyoizumi T, Pfister JP, Aihara K, Gerstner W. Spike-timing dependent plasticity and mutual information maximization for a spiking neuron model. In Advances in neural information processing systems 2005 (pp. 1409–1416).
10.
Yu L, Yu Y. Energy‐efficient neural information processing in individual neurons and neuronal networks. Journal of Neuroscience Research 2017 Nov;95(11):2253–66.

P144 Hierarchical inference interactions in dynamic environments

Zachary Kilpatrick¹, Tahra Eissa¹, Nicholas Barendregt¹, Joshua Gold², Kresimir Josic³

¹University of Colorado Boulder, Applied Mathematics, Boulder, Colorado, United States of America; ²University of Pennsylvania, Neuroscience, Philadelphia, Pennsylvania, United States of America; ³University of Houston, Mathematics, Houston, United States of America

Correspondence: Zachary Kilpatrick (zpkilpat@colorado.edu)

BMC Neuroscience 2019, 20(Suppl 1):P144

In a constantly changing world, accurate decisions require flexible evidence accumulation. As old information becomes less relevant, it should be discounted at a rate adapted to the frequency of environmental changes. However, sometimes humans and other animals must simultaneously infer the state of the environment and its volatility (hazard rate). How do such inference processes interact when performed hierarchically? To address this question, we developed and analyzed a model of an ideal observer who must report either the state or the hazard rate. We find that the speed of both state and hazard rate inference is mostly determined by information integration across change points.

Our observer infers the state and hazard rate by integrating noisy observations and discounting them according to an evolving hazard rate estimate. To analyze this model and its variants, we developed a new method for computing the observer’s state and hazard rate beliefs. Instead of sampling, we solve a set of nonlinear partial differential equations (PDEs), leading to faster and more accurate estimates. We characterize how optimal and suboptimal (those with mistuned evidence discounting rates or other discounting functions) observers infer the state and hazard rate and compare their performance in tasks with varying difficulty. Suboptimal observers may possess mistuned evidence discounting rates or even different functional forms of discounting.

Evidence near change points strongly perturbs an observer’s posterior by altering the state belief and supports higher hazard rates. Thus, state and hazard rate inference are linked, and the speed of hazard rate learning is primarily determined by how well the observer accounts for change points. Early in a trial, changes may not be well tracked, as the observer’s hazard rate estimate is poor, but this estimate improves as the trial evolves, and environmental changes are better tracked.

We measure how biases in hazard rate learning influence an observer’s state inference process. Our setup can therefore be used to improve dynamic decision task design by identifying parameterizations that reveal hierarchical inference strategies.

Acknowledgements: We thank a grant from NIH in Collaborative Research in Computational Neuroscience for supporting Zachary Kilpatrick, Tahra Eissa, and Nicholas Barendregt with R01MH115557-01.

P145 Optimizing sequential decisions in the drift-diffusion model

Khanh Nguyen¹, Zachary Kilpatrick², Kresimir Josic¹

¹University of Houston, Mathematics, Houston, TX, United States of America; ²University of Colorado Boulder, Applied Mathematics, Boulder, CO, United States of America

Correspondence: Khanh Nguyen (kpnguyen@math.uh.edu)

BMC Neuroscience 2019, 20(Suppl 1):P145

Natural environments change over many different timescales. To make the best decisions organisms must therefore flexibly accumulate information, accounting for what is relevant, and ignoring what is not. However, many experimental and modeling studies of decision-making focus on sequences of independent trials. In such studies, both the evidence gathered to make a choice and the resulting actions are irrelevant to future decisions. To understand decision-making under more natural conditions, we propose and analyze models of observers who accumulate evidence to freely make choices across a sequence of correlated trials, and receive uncertain feedback.

Two alternative forced choice tasks are often used to identify strategies humans and other animals use to make decisions. Experiments have shown that subjects can learn the latent probabilistic structure of the environment to increase their performance. However, a lack of systematic analyses of normative models makes it difficult to study whether and how subjects’ decision-making strategies deviate from optimality. To address this problem, we extend drift-diffusion models to obtain the normative form of evidence accumulation in serial trials whose correct choice evolves as a two-state Markov process. Ideal observers integrate noisy evidence within a trial until reaching a decision threshold. Their initial belief is biased by their choice and feedback on previous trials. If observers use fixed decision thresholds, their bias decreases decision times, but leaves the probability of correct answers unchanged. To optimize reward rate in trial sequences, ideal observers adjust their thresholds over trials to deliberate longer on early decisions, and respond more quickly later in the sequence. We show how conflicts between unreliable feedback and evidence from previous trials are resolved by marginalization. Our findings are consistent with experimentally observed response trends, suggesting humans often assume correlations in task environments even when none exist.

P146 Degeneracy in hippocampal CA1 neurons

Rosanna Migliore¹, Carmen Alina Lupascu¹, Luca Leonardo Bologna¹, Armando Romani², Jean-Denis Courcol², Werner Alfons Hilda Van Geit², Alex M Thomson³, Audrey Mercer³, Sigrun Lange³, Christian A Rössert², Ying Shi², Olivier Hagens², Maurizio Pezzoli², Tamas Freund⁴, Eilif Muller², Felix Schuermann², Henry Markram², Michele Migliore¹, Stefano Antonel², Joanne Falck³, Szabolcs Kali⁴

¹Institute of Biophysics, National Research Council, Italy; ²École Polytechnique Fédérale de Lausanne, Blue Brain Project, Lausanne, Switzerland; ³University College London, London, United Kingdom; ⁴Institute of Experimental Medicine, Hungarian Academy of Sciences, Hungary

Correspondence: Rosanna Migliore (rosanna.migliore@cnr.it)

BMC Neuroscience 2019, 20(Suppl 1):P146

Every neuron of a network exerts its function by transforming multiple spatiotemporal synaptic input patterns into a single spiking output. During development and during the entire lifetime of a neuron, its input/output function is adapted to realize ongoing refinement of the function of the neuron and circuit, or maintain functional robustness in the face of constant protein turnover or an evolving pathological condition. This process results in a high variability in the observed peak conductance of ion channels across neurons. The mechanisms responsible for this variability are not well understood, although there are clear experimental and modeling indications that correlation and degeneracy among a variety of conductances can be involved.

Here, using a unified data-driven simulation workflow [1, 2], we studied this issue in -detailed models of hippocampal CA1 pyramidal cells and interneurons with morphological and electrophysiological properties explicitly constrained with experimental data from rats [3].

The models and their analysis show that the set of conductances expressed in any given hippocampal neuron may be considered as belonging to two groups: one subset is responsible for the major characteristics of the firing behavior in each population and the other more involved in degeneracy. It is also possible to conceive several experimentally testable predictions related to the combination and relative proportion of the different conductances that should be expressed on the membrane of different types of neurons for them to fulfill their role in the hippocampus circuitry.

References

1.
This modeling effort has been carried out using the Brain Simulation Platform (https://collab.humanbrainproject.eu/#/collab/1655/nav/28538) and two open-source packages, the Electrophys Feature Extraction Library (eFEL, https://github.com/BlueBrain/eFEL) and the Blue Brain Python Optimization Library (BluePyOpt) developed within the Human Brain Project (https://www.humanbrainproject.eu/en/).
2.
Van Geit W, Gevaert M, Chindemi G, et al. BluePyOpt: Leveraging Open Source Software and Cloud Infrastructure to Optimise Model Parameters in Neuroscience. Frontiers in Neuroinformatics 2016, 10: 17. https://doi.org/10.3389/fninf.2016.00017
3.
Migliore R, Lupascu CA, Bologna LL, et al. The physiological variability of channel density in hippocampal CA1 pyramidal cells and interneurons explored using a unified data-driven modeling workflow. PLoS Computational Biology 2018. 14(9): e1006423. https://doi.org/10.1371/journal.pcbi.1006423

P147 Mechanisms of combined electrical and optogenetic costimulation

William Hart¹, Paul Stoddart¹, Tatiana Kameneva²

¹Swinburne University of Technology, ARC Centre for Biodevices, Melbourne, Australia; ²Swinburne University of Technology, Telecommunication Electrical Robotics and Biomedical Engineering, Hawthorn, Australia

Correspondence: Tatiana Kameneva (tkameneva@swin.edu.au)

BMC Neuroscience 2019, 20(Suppl 1):P147

Neuroprosthetic devices are reaching a level of maturity and have benefited many people who suffer from neurological conditions such as deafness and blindness. However, the perception outcome that they provide is significantly less than normal function. In part, this is due to the current spread, neural adaptation and inability to selectively activate different classes of neurons when using electrical stimulation. Optogenetic neural stimulation may provide an alternative to conventional electrical pulse stimulation by delivering more targeted stimulation with higher spatial resolution. A novel way to stimulate neurons is to combine conventional electrical stimulation with targeted optogenetic stimulation. The mechanisms of neural activation in response to the combined electrical and optogenetic costimulation are not clear.

To investigate the mechanisms of neural activation in response to electrical and optogenetic costimulation, we used computer simulations in the NEURON environment. We simulated single compartment neurons and used Hodgkin-Huxley type formalism to study how costimulation and a combination of ionic channels affect the neuronal response. To simulate an optogenetically modified neuron, we combined voltage-activated currents with a model of channelrodopsin-2 ion channel responsive to voltage, temperature and light. We systematically applied different levels of intracellular current pulse stimulation and optical stimulation to bring the membrane potential close to firing threshold. We also applied mock-electrical current stimulation that approximates the response of neurons to optical-alone stimulation and studied the activation of ionic channels in this case. To isolate the mechanisms during costimulation, the maximum sodium conductance in the NEURON model was set to zero, simulating total blockage of sodium channels.

Our results showed that the membrane is initially depolarised by a small inward channelrhodopsin current during the optical stimulation, followed by a rapid sodium current following the electrical trigger. During costimulation, the channelrhodopsin current transiently reduced during the action potential due to its voltage sensitivity. This result matched modelling and experimental data reported by [1] in cardiomyocytes.

Our results support the interpretation of a costimulation mechanism involving two separate families of ion channels. Our results may have implications for the development of stimulation strategies in novel neurosprosthetic devices that have electrical and optogenetic stimulation capabilities.

Reference

1.
Williams JC, Xu J, Lu Z, et al. Computational optogenetics: empirically-derived voltage-and light-sensitive channelrhodopsin-2 model. PLoS computational biology 2013 Sep 12;9(9):e1003220.

P148 Real-time Bayesian decoding of taste from neural populations in gustatory cortex

Daniel Svedberg, Bradly Stone, Donald Katz

Brandeis University, Department of Neuroscience, Waltham, MA, United States of America

Correspondence: Daniel Svedberg (dsvedberg@brandeis.edu)

BMC Neuroscience 2019, 20(Suppl 1):P148

The activity of neural ensembles in gustatory cortex encodes various features of gustatory stimuli in a temporally dynamic fashion, using adaptive coding schemes. Although it is well-established that electrophysiological activity of neural ensembles in gustatory cortex differentiates the identities of basic tastes over many taste exposures, it is unknown if taste can be statistically and reliably identified from individual trials, on an instantaneous basis. Rats were implanted with a multielectrode drive in gustatory cortex and were given oral deliveries of liquids with one of each of the basic tastes. Here we demonstrate that a naïve Bayesian decoder can reliably decode tastes from populations of neurons on an instantaneous basis, evaluate various strategies for establishing sampling periods, and compare dynamics of Bayesian decoding against dynamic state transitions identified by Hidden Markov Modeling.

P149 Effects of value on early sensory activity and motor preparation during rapid sensorimotor decisions

L. Alexandra Martinez-Rodriguez, Simon P. Kelly

University College Dublin, School of Electrical & Electronic Engineering, Dublin, Ireland

Correspondence: L. Alexandra Martinez-Rodriguez (l.martinezrodriguez@ucdconnect.ie)

BMC Neuroscience 2019, 20(Suppl 1):P149

Various computational accounts have been proposed to explain how sensorimotor decisions are biased by value. Although the longstanding dominant account has been the Starting Point Bias model, where the starting point of an evidence-accumulating decision variable is shifted towards the higher value decision bound, our group recently showed that fast biased decisions are best explained by a Drift Rate Bias model when one allows for temporally increasing drift rate [1] Such drift rate biases may arise directly from the modulation of the sensory representations of evidence in low-level sensory cortex. Alternatively, they may be implemented through post-sensory modulations, in which case they would be expressed in motor preparation dynamics but not in sensory encoding. Our study examines this by recording EEG (Biosemi), eye-position (Eyelink) and EMG of the flexor policis brevis muscle during a value-biased orientation discrimination task under a strict deadline, where a correct response to one orientation was worth more (40 points) than the other (10).

As expected, errors were more frequent (p<.001) and were committed with greater haste (p<.01) on low value trials such that the fastest responses were purely value driven and the slowest entirely sensory-driven (hence correct). Replicating Afacan et al, a Dynamic Drift Rate Bias model, in which drift rate is biased by value and is non-stationary, increasing over the short decision time frame, fit the behavioural data better than models with stationary evidence and/or starting point bias.

Neurophysiological analyses revealed that the initial “C1” component of the visual evoked potential (VEP), thought to reflect primary visual cortical activation, showed no signs of significant value modulation (p>.1) for either correct responses or for errors. A Starting Point bias mechanism around target onset was observed in the Lateralized Readiness Potential (LRP), across the different value conditions. Interestingly, this starting point bias seemed to increase with time (Fig. 1).

Given that the best fitting model included a drift rate bias but our results showed that value does not modulate the earliest sensory evidence, this bias must be implemented at a later processing stage. It could be that these biases are implemented at the motor level, taking the form of urgency signals. The slopes of the urgency signals and their onsets could vary according to the value of the stimulus. In order to test this hypothesis, a new model was created which included an urgency signal with a different start time and rate of increase for each value condition. This Dynamic Urgency model proved to fit the data as well as the Dynamic Drift Rate Bias model did. Further, these urgency signals can account for an initially negative drift rate as well as the temporally growing Starting Point Bias observed in the Lateralized Readiness Potential. These findings further demonstrate the inadequacy of standard stationary-accumulation models in explaining highly time-constrained, value-biased decisions, and highlight novel computational architectures that may explain the more complex decision formation dynamics unfolding in such scenarios, which are prevalent in real life.

Reference

1.
Afacan-Seref K, Steinemann NA, Blangero A, Kelly SP. Dynamic interplay of value and sensory information in high-speed decision making. Current Biology 2018 Mar 5;28(5):795–802.

P150 A real-time model fitting method for single individual neurons

Felix B. Kern¹, Thomas Nowotny², George Kemenes¹

¹University of Sussex, School of Life Sciences, Brighton, United Kingdom; ²University of Sussex, School of Engineering and Informatics, Brighton, United Kingdom

Correspondence: Felix B. Kern (fbk21@sussex.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P150

Most currently available methods of constructing conductance-based biophysical models of neuronal activity are not suitable for finding valid descriptions of live individual neurons. Often, data from several neurons of a given type, e.g. pharmacologically separated currents, are pooled to yield a single model, ignoring the cells’ unique morphology and, as has been shown to be the case in at least some invertebrate neurons, individual differences in current expression. Alternatively, electrophysiological data from a single neuron are combined with morphological reconstruction of that same neuron to yield a highly accurate model of a single cell at the price of a process spanning many days or weeks. In neither case does the resulting model match a living, experimentally accessible neuron.

In order to probe e.g. the dynamics of small neuronal circuits, or to track changes in neuronal properties over time induced e.g. by intrinsic plasticity, cellular homoeostasis, or extrinsic modulation of ion channels, it would be desirable to have an accurate model of the cell under investigation while the experiment is ongoing. Here, we present a novel method that attempts to solve this problem. Rather than separating currents pharmacologically, we use a machine learning approach to design highly informative voltage clamp stimulation protocols in advance of an experiment, guided by an informed guess about how the model might be structured and parametrised. Using these stimulations and a massively parallel optimisation algorithm, we rapidly arrive at model parameters that accurately reflect the properties of the membrane and its active conductances. We show a proof of concept for single-compartment models in simulation and in a model system and discuss advantages and limitations of the method.

P151 S1 neurons process spontaneous pain information using nonlinear distributed coding

Sa-Yoon Park¹, Heera Yoon², Sun Kwang Kim², Sang Jeong Kim³, Chang-Eop Kim⁴

¹Gachon University, Department of Physiology, Seongnam, South Korea; ²Kyung Hee University, Department of Physiology, Seoul, South Korea; ³Seoul National University, Department of Physiology, Seoul, South Korea; ⁴Gachon Uniersity, Department of Physiology, Seoul, South Korea

Correspondence: Sa-Yoon Park (sayou92@naver.com)

BMC Neuroscience 2019, 20(Suppl 1):P151

The coding principle of pain has been debated between two opposing ideas for decades—labeled line coding and distributed coding. Further, according to the way of distribution, distributed coding can be categorized as linear distributed and non-linear distributed coding. Noxious information is well known to be conveyed at a peripheral level via independent neural pathways, such as C and A-delta fibers. However, it remains largely unknown how the neural circuits at the spinal and supraspinal level process pain information. Here, we examined whether primary somatosensory (S1) neurons process various properties of spontaneous pain and further, how S1 neurons encode pain information in terms of computational coding principle. We recorded activities of neural populations in the S1 cortex from awake head-fixed mice during formalin-induced pain using in vivo two-photon Ca2+ imaging (n = 7). Subcutaneously injected formalin elicits a biphasic pain-related behavior, i.e. a short early phase around 0–5 min, a longer period of late phase around 20–60 min, and interphase showing minimum pain-related behavior between them. To capture the dynamics of neural activities during each phase, Ca2+ imaging was performed before injection, 1–3 min, 7–9 min, 25–27 min, and 43–45 min after injection periods (basal, early, inter, late 1, and late 2 phase). First, we computed the preference index (PI) of neurons for each phase and compared those between different phases using PI scatter plots. A distinct population of neurons with different preference for each phase was observed, implying the response of S1 neurons to noxious information from the periphery during each phase is not one-dimensional. To establish whether the neuronal population of S1 cortex supports labeled line coding or distributed coding, we conducted multiple linear regression analysis with Ca2+ signals of each neuron as the outcome and binary phase information as the predictors. Most neurons (446/468) showed more than two significant beta coefficients for phases, suggesting that S1 neurons encode multiple phase information (distributed coding) rather than tuned to a specific phase. To examine the way S1 neurons distribute pain information, we first applied support vector machine (SVM) classifier with linear kernel, and successfully decoded the phase information using the neural activity of the population (average multiclass classification accuracy of 0.88, 10-fold cross-validation). We then removed all the linear components of the neural signals with respect to the phase information by orthogonalizing them. SVM with the non-linear kernel using this orthogonalized residuals still achieved significant decoding performance for each phase (average performance of decoding was 0.77, 10-fold cross-validation), while linear SVM did not. Taken together, these results suggest that S1 neurons process each phase of the spontaneous pain information using both linear and non-linear distributed coding schemes, rather than labeled line coding scheme.

P152 Dynamic Worm: Computational investigation of locomotion through integration of connectomics, neural dynamics and biomechanics in C. elegans

Eli Shlizerman^1,2, Jimin Kim²

¹University of Washington, Departments of Applied Mathematics, Seattle, WA, United States of America; ²University of Washington, Electrical & Computer Engineering, Seattle, United States of America

Correspondence: Eli Shlizerman (shlizee@uw.edu)

BMC Neuroscience 2019, 20(Suppl 1):P152

The ability to discern how the brain orchestrates behavior relies on the development of successful computational approaches to link and analyze outcomes of multi-pronged investigations of the nervous system. We have developed such an integrative approach for the nematode Caenorhabditis elegans (C. elegans). Specifically, we propose a model which emulates the full somatic nervous system and its response to stimuli. The model incorporates the anatomical wiring diagram, connectome of 279 neurons, and intra-cellular and extra-cellular neural dynamics. In addition, it includes layers which translate neural activity to muscle forces and muscle impulses to body postures. The model also implements an inverse integration procedure which modulates neural dynamics according to external forces on the body. We validate the model by injecting currents into sensory- and inter- neurons and by applying external forces to the body.

We are able to generate locomotion behaviors typical to the nematode (forward and backward) from neural stimuli or body forces. The characteristics of the movements are similar to experimentally identified ones. Furthermore, the neural dynamics associated with distinct movements can be mapped and classified using low dimensional embeddings. Accordingly, these results show that our model, and thus the connectome along with neural dynamics, encompass rhythmic activity and locomotion behaviors. Utilizing the inverse integration approach, we simulate the effect of environmental forces acting on the body through proprioceptive feedback and show that feedback can entrain and sustain movements initiated by neural or mechanical triggers. Taken together, our results show that the structure of the connectome sets specific movement patterns for the organism. These patterns are enabled by neural dynamics guided by the connectome.

The success of the dynamic worm framework to generate robust directional locomotion warrants the development of computational approaches utilizing it for identification of neural circuits and pathways associated with specific neural stimuli. We demonstrate that such studies are plausible. We apply neural stimuli experimentally known to modulate locomotion and trigger behavioral responses such as turns, escape and avoidance and show that our model supports them. We then propose computational ablation strategies, particularly (i) ablation survey and (ii) conditional ablation, for inferring neural pathways associated with these stimuli. Specifically, we demonstrate how ablation survey of all inter-neurons reveals command neurons that facilitate sensory-motor responses, such as SMDV in a sharp turn response to RIV stimulation. We also show how conditional ablation can identify alternative pathways to known command neurons and facilitate steering away behavior in the case of olfactory asymmetric neural stimuli.

In conclusion, our study provides a novel computational approach to study the interaction between the brain and behavior in C. elegans. Specifically, the dynamic worm framework incorporates models of interacting layers of the nervous system and bio mechanics and shows their critical role in generating locomotion movements. The outcomes of our study show that such framework can be utilized to identify brain circuits which control, mediate and generate natural behavior.

P153 Inhibitory structures may interrupt the coherence of slow activity in deep anesthesia

Pangyu Joo, Seunghwan Kim

Pohang University of Science and Technology, Physics Department, Pohang, South Korea

Correspondence: Pangyu Joo (pangyu32@postech.ac.kr)

BMC Neuroscience 2019, 20(Suppl 1):P153

EEG has been utilized as an important means of investigation on anesthetized brain because it instantaneously reflects the change in distinct brain dynamics during anesthesia. EEG during deep anesthesia is usually characterized by prominent slow oscillatory activities: slow oscillation and burst suppression. Slow oscillation and burst suppression have significantly different EEG patterns and therefore it may seem inconsistent with the studies that slow oscillation and burst suppression have qualitatively similar active-inactive patterns in neuronal level.

Our assumption is that the difference comes from synchronization of slow activity of the brain. Slow oscillation is known to be fragmentized across cortex. On the other hand, burst suppression is mainly global phenomena although it has some significant local characteristics. Moreover, the cortex is known to be hyper-excitable so that a small excitation can propagate over the cortex during burst suppression period. To sum up, we can hypothesize that spatially incoherent slow oscillation may turn into spatially coherent burst suppression due to the cortical hyper-excitability caused by reduced inhibition during burst suppression period.

We suggest two inhibitory structures which may prohibit spatial synchronization of slow activities. The two possible inhibitory structures we suggest are overlapped inhibitions and inter-inhibitory connectivity and we constructed a computational model to verify the effect of the structures. First of all, we studied the two possible inhibitory structure on a 1D chain of neurons which is divided into two modules. We found that the additional inhibitory structures on the model can disturb the coherence of slow activities. With these inhibitory structures, we constructed more realistic model where the neurons are distributed in finite space and the neurons are linked each other with probabilities depending on the distance between each neuron. In the models, the inhibitory structure could interrupt the spatial coherence of slow activities, and the degree of incoherence was dependent on the interaction range of inhibitory neurons. Also simulated EEG derived from the model exhibits several characteristics which can be generally observed in transition period between slow oscillation and burst suppression (see Fig. 1). These results suggest that inhibitory neuron can disturb the coherence of slow activities in deep anesthesia and the transition between slow oscillation and burst suppression may governed by disturbance of synchronization by inhibitory structures.

P154 Data-driven predictive models for information processing in the small brain of Caenorhabditis elegans

Chentao Wen, Kotaro Kimura

Nagoya City University, Graduate School of Natural Sciences, Nagoya, Japan

Correspondence: Chentao Wen (chintou.on@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P154

The brain perceives information from external environments, extracts critical aspects of the information and integrates them to make decisions and regulates behaviors. How can the network of multiple neurons in the brain substantiate such sophisticated functions? Previous modelling studies focused on those large brains, e.g. in human and rodents, which are too complex to obtain accurate understanding. In contrast, recent fast 3D optical monitoring of all neuronal activities (whole brain imaging) in small brains such as zebrafish and the nematode Caenorhabditis elegans has allowed us to model brain activities accurately. However, these studies were mostly based on “compressed” data from principal component analysis, or simply applied correlation analyses, which cannot reveal accurate “information flow” in the brain. Here we modelled activities of all head neurons (~150) in C. elegansacquired by whole brain imaging [1]. Our data-driven models using machine learning techniques were able to predict individual neuronal activities by its own history and effects from other neurons, thus accurately described the potential ways of information processing in the brain. We found the tree-based models and support vector regression model are more accurate than simple linear model, while the long short-term memory (LSTM) predicts poor. Furthermore, we estimated the “causality” from our models by estimating the importance of predictors in each model. Although the estimated importance from different models are somewhat variant in details, usually those most important predictors were commonly chosen. To reveal the commonality and differences between anatomical and functional neural network, we will compare those “causality” patterns with connectome information [2] and will test our results by experimentally perturbing neuronal activities with optogenetics techniques. Our studies suggest that machine learning-based modeling of neuronal activities can reveal the patterns of information processing in small brains and may be used for understanding large brains in future.

References

1.
Wen C, Miura T, Fujie Y, Teramoto T, Ishihara T, Kimura KD. Deep-learning-based flexible pipeline for segmenting and tracking cells in 3D image time series for whole brain imaging. bioRxiv 2018 Jan 1:385567.
2.
White JG, Southgate E, Thomson JN, Brenner S. The structure of the nervous system of the nematode Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci. 1986 Nov 12;314(1165):1–340.

P155 A neural network model of naming impairment and treatment response in bilingual speakers with aphasia

Claudia Penaloza¹, Uli Grasemann², Maria Dekhtyar¹, Risto Miikkulainen², Swathi Kiran¹

¹Boston University, Department of Speech, Language and Hearing Sciences, Boston, United States of America; ²University of Texas at Austin, Department of Computer Science, Austin, United States of America

Correspondence: Claudia Penaloza (penaloza@bu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P155

Bilinguals with aphasia (BWA) may present varying degrees of impairment in their two languages, yet both languages have potential for recovery [1]. Computational models that simulate treatment outcomes in BWA can help predicting which language should be targeted in treatment to observe the maximum potential treatment gains in both languages. Here we aimed to simulate (i) naming impairment in the native (L1) and the second language (L2) and (ii) treatment effects in the treated language and cross-language transfer effects in the untreated language in BWA. Based on our previous DISLEX model [1] we developed BiLex, a neural network model of bilingual lexical access based on self-organizing maps SOMS, that can simulate L1 and L2 naming ability in healthy bilinguals with varying degrees of language proficiency [2]. First, we trained an individual instance of the BiLex model for 13 Spanish-English BWA (mean age = 55.61 years) whose data have been previously reported elsewhere [1, 3] to simulate their naming abilities prior to stroke while accounting for their age at testing, L2 age of acquisition and L1 and L2 prestroke exposure. Next, these individual models were lesioned by gradually applying increasing amounts of damage to simulate independently the L1 and L2 naming deficits observed in standardized language tests in each BWA. Finally, each individual model was retrained to simulate treatment outcomes in the treated and the untreated language (Fig. 1). All BWA received naming treatment based on semantic feature analysis in English (n = 6) or Spanish (n = 7), and their treatment outcomes were estimated by computing effect sizes [4] on the treated and the untreated language. Significant treatment gains were observed in 10 BWA in the treated language (English n = 4; Spanish n = 6) and 3 BWA also presented significant cross-language transfer effects to the untreated language. Cross-correlations between behavioral treatment and computational model times-series data for the treated (range: 0.48 to 0.96) and the untreated language (range: −0.15 to 0.63) suggest that overall, BiLex can capture treatment effects in the language targeted in therapy for most BWA, and cross-language transfer for BWA presenting treatment gains in the untreated language. In future research, these simulations can be employed to evaluate potential treatment gains in each language and to guide clinical decisions on the language that should be targeted in treatment with BWA.

Acknowledgments: We thank the National Institute on Deafness and Other Communication Disorders of the National Institutes of Health for supporting Swathi Kiran with grant U01DC014922.

References

1.
Kiran S, Grasemann U, Sandberg C, Miikkulainen R. A computational account of bilingual aphasia rehabilitation. Bilingualism: Language and Cognition 2013 Apr;16(2):325–42.
2.
Peñaloza C, Grasemann U, Dekhtyar M, et al. BiLex: A computational approach to the effects of age of acquisition and language exposure in bilingual lexical access. Brain and Language, In press.
3.
Kiran S, Sandberg C, Gray T, Ascenso E, Kester E. Rehabilitation in bilingual aphasia: Evidence for within-and between-language generalization. American journal of speech-language pathology 2013.
4.
Beeson PM, Robey RR. Evaluating single-subject treatment research: Lessons learned from the aphasia literature. Neuropsychology Review 2006 Dec 1;16(4):161–9.

P156 Modeling hindlimb elevation angles during intact locomotion and locomotion evoked by MLR- and epidural spinal stimulation in decerebrate cats

Boris Prilutsky¹, Ilya Rybak², Sergey Markin², Pavel Zelenin³, Tatiana Deliagina³, Yury Gerasimenko⁴, Pavel Musienko⁵, Alexander Klishko⁶

¹Georgia Institute of Technology, Biological Sciences, Atlanta, GA, GA, United States of America; ²Drexel University, Anatomy and Neurobiology, Philadelphia, United States of America; ³Karolinska Institutet, Department of Neuroscience, Stockholm, Sweden; ⁴University of California, Los Angeles, Integrative Biology and Physiology, Los Angeles, United States of America; ⁵Pavlov Institute of Physiology, Motor Physiology Laboratory, St. Petersburg, Russia; ⁶Georgia Tech, Marietta, GA, United States of America

Correspondence: Boris Prilutsky (boris.prilutsky@ap.gatech.edu)

BMC Neuroscience 2019, 20(Suppl 1):P156

It has been suggested that in order to overcome the motor redundancy of the mammalian musculoskeletal system and simplify motor control, the nervous system imposes neural constraints on redundant degrees of freedom. For example, during the cycle of locomotion, the three elevation angles of leg segments (Fig. 1B) are constrained to form a loop in a plane—the kinematic synergy of planar covariation of elevation angles. The origin of these neural constraints in the nervous system is unknown.

Here, we addressed this question by computational and experimental studies of planar covariation of hindlimb segmental elevation angles during intact locomotion and during locomotion of decerebrate cats evoked by electrical stimulation of the mesencephalic locomotor region (MLR) in the brainstem and by epidural stimulation (ES) of the spinal cord at L6–L7. Possible differences in the planar covariation between intact and MLR-evoked locomotion could indicate the potential contribution of the forebrain in imposing the neural constraints. Differences in planarity between MLR- and ES-evoked locomotion would suggest the role of motion-dependent sensory feedback, which is partially disrupted by ES. If a neuromechanical model of spinal control of locomotion (Fig. 1A) reproduced the elevation angle planarity, this result would suggest that spinal locomotor circuits may be responsible for the neural constraints on the hindlimb elevation angles. We modelled electrical MLR and ES stimulations as excitatory tonic inputs to spinal interneurons representing the CPG network and afferent motion-dependent pathways, respectively. We tuned these inputs to reproduce EMG activity of major hindlimb muscles recorded during MLR-evoked and ES-evoked locomotion. Planarity of elevation angle trajectories was quantified by the percentage of total data variation (PV) accounted for by the first two principal components describing the data. Thus, the complete planarity occurred when PV = 100%.

We found that all three walking conditions exhibited planar covariation of elevation angles (Fig. 11C). There was no significant difference in planarity between the MLR-evoked (PVMLR = 99%) and ES-evoked (PVES = 99%) walking and intact walking (PVInt = 98%; Fig. 1C). Since the circuitry in the spinal cord and brainstem lead to planar covariation, the forebrain does not appear to contribute to the neural constraints on the elevation angles. The neuromechanical model of spinal locomotor control reproduced planar trajectories of the elevation angles for MLR-evoked (PVMLR_m = 97%), ES-evoked (PVES_m = 98%) and intact (PVInt_m = 98%) walking (Fig. 1D). Analysis of the model suggested that neural constraints on elevation angles may originate from the CPG periodic activity.

Acknowledgements: Supported by NIH grantR01 NS100928.

P157 How do local neural populations know about the predictability of sound sequences

Shih-Cheng Chien¹, Burkhard Maess¹, Thomas Knoesche²

¹Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany; ²MPI for Human Cognitive and Brain Sciences, Department of Neurophysics, Leipzig, Germany

Correspondence: Shih-Cheng Chien (vchien@cbs.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):P157

The brain recognizes regularity of trains of sound sequences soon after a few repetitions. A MEG study showed that the predictability of sound sequences is positively correlated to the root mean square (RMS) amplitude of the MEG signals: the participants showed higher RMS amplitude when passively listening to regular than random, and short than long sound sequences [1]. This finding is counterintuitive in the context of predictive-coding because the prediction error is assumed to decrease under more predictable conditions (i.e., regular and short sequences). Auksztulewicz and colleagues included synaptic gain modulation in their dynamic causal modeling (DCM) to account for the change in RMS amplitude [2]. However, how the synaptic gain is modulated according to the predictability is not clear. In order to clarify this, we investigate how the dynamics of neural activities and change in synaptic strength in a local neural network (representing the primary auditory cortex) may be reshaped by sound sequences under conditions of different predictability.

We construct a rate-based primary auditory cortex model that consists of excitatory (E) and inhibitory (I) neural populations, where all E populations receive external inputs in tonotopic manner. Three short-term plasticity rules are considered: (1) synaptic adaptation on E-to-E connections, (2) Hebbian learning on E-to-E connections, and (3) Hebbian learning on E-to-I connections. The 1st plasticity rule reduces the synaptic strength according to the pre-synaptic activity [3]. The 2nd and 3rd plasticity rules increase/reduce the synaptic strength according to the temporal order of firing activities between the populations [4]. The simulation results show that the 1st plasticity rule (i.e. adaptation) alone can account for the higher neural activity in regular than random sequences, but cannot account for the higher neural activity in short than long sequences, if the 2nd and 3rd plasticity rules (i.e. Hebbian learning) are not considered.

We demonstrate how synaptic gain is modulated (as suggested by [2]) during predictable sequences, which potentially links RMS amplitude and predictability of sound sequences. This study provides a possible mechanism of reshaping the synaptic strength and firing activities when only local information is available.

References

1.
Barascud N, Pearce MT, Griffiths TD, Friston KJ, Chait M. Brain responses in humans reveal ideal observer-like sensitivity to complex acoustic patterns. Proceedings of the National Academy of Sciences 2016 Feb 2;113(5):E616–25.
2.
Auksztulewicz R, Barascud N, Cooray G, Nobre AC, Chait M, Friston K. The cumulative effects of predictability on synaptic gain in the auditory processing stream. Journal of Neuroscience 2017 Jul 12;37(28):6751–60.
3.
May PJ, Tiitinen H. Mismatch negativity (MMN), the deviance‐elicited auditory deflection, explained. Psychophysiology 2010 Jan;47(1):66–122.
4.
Caporale N, Dan Y. Spike timing–dependent plasticity: a Hebbian learning rule. Annu. Rev. Neurosci. 2008 Jul 21;31:25–46.

P158 Action potential propagation in long-range axonal fiber bundles

Helmut Schmidt¹, Thomas Knoesche²

¹Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany; ²MPI for Human Cognitive and Brain Sciences, Department of Neurophysics, Leipzig, Germany

Correspondence: Helmut Schmidt (hschmidt@cbs.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):P158

With the advent of advanced MRI techniques, it has become possible to study the white matter non-invasively and in great detail. Estimating important parameters of long-range connections, such as axon diameters and myelin thickness, enables building and refining computational models of the brain that incorporate detailed effects of long-range transmission, such as distributed delays and synchronisation. If one wants to study large networks (possibly of the entire brain) and systematically investigate their parameter spaces, we need a mathematical description of action potential propagation that is sufficiently simple, yet still biologically plausible. We developed a mathematical framework that can achieve this by using a leaky integrate-and-fire framework with passive sub-threshold dynamics and explicit threshold-activated ion currents. We study different types of ion current profiles ranging from instantaneous currents modelled by delta functions, to combinations of exponential functions describing ion current profiles found experimentally. This framework allows us to derive explicit solutions for the depolarisation / hyperpolarisation profiles of action potentials. We use these to study in detail the influence of the various, potentially MRI derived, model parameters on action potential velocity. We also use this framework to study the synchronisation of action potentials between ephaptically coupled axons.

Specifically, we recover known results regarding the influence of axon diameter, node of Ranvier length and internode length on the velocity of action potentials. The velocity scales approximately linearly with the diameter in myelinated axons, and with the square root of the diameter in unmyelinated axons [1]. The velocity shows a maximum at values of node and internode length in myelinated axons that correspond to experimentally observed values [2, 3], thus suggesting that the axonal microstructure is optimised for high velocities. Furthermore, we find that the velocity depends more strongly on the thickness of the myelin sheath than was suggested by previous theoretical studies [1]. In addition, we explain the slowing down and synchronisation of action potentials in ephaptically coupled fibers through changes in the effective electrotonic length constant. We see the same effect of threshold perturbation within passive fibres by action potentials passing through neighbouring axons that has been observed experimentally [3]. Finally, we use our results to derive the delay distribution between brain regions given a specific distribution of axonal diameters within a fibre bundle. In summary, we present a solution for incorporating detailed axonal properties into a whole-brain modelling framework.

References

1.
Rushton WAH. A theory of the effects of fiber size in medullated nerve. J. Physiol. 1951, 115, 101–122.
2.
Hursh JB. Conduction velocity and diameter of nerve fibers. Am. J. Physiol. 1939, 127, 131–139.
3.
Arancibia-Carcamo IL, et al. Node of Ranvier length as a potential regulator of myelinated conduction speed. eLife 2017, 6, e23329.
4.
Katz B, Schmitt OH. Electric interaction between two adjacent nerve fibers. J. Physiol. 1940, 97, 471–488.

P159 From damped oscillations to synchronous bursting: Describing the effects of synaptic depression on the collective behavior of spiking neurons

Richard Gast¹, Helmut Schmidt², Harald Möller³, Nikolaus Weiskopf³, Thomas Knoesche³

¹MPI for Human Cognitive and Brain Sciences, MEG and Cortical Networks Group, Nuclear Magnetic Resonance Group, Neurophysics Department, Leipzig, Germany; ²Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany; ³MPI for Human Cognitive and Brain Sciences, Department of Neurophysics, Leipzig, Germany

Correspondence: Richard Gast (rgast@cbs.mpg.de)

BMC Neuroscience 2019, 20(Suppl 1):P159

From a dynamical systems point of view, the brain can be described as a complex system consisting of a vast number of interacting, non-linear units, i.e. neurons. One prominent approach to study this system is to describe the collective behavior of large neural populations instead of the behavior of each single neuron [1, 2].Crucial to this approach is the availability of proper macroscopic descriptions of the collective behavior of interacting neurons. In a recent study, Montbrio and colleagues analytically derived a mathematically exact description of the macroscopic firing rate and membrane potential dynamics of a fully coupled population of quadratic integrate-and-fire neurons (QIF) [3]. While simple excitatory-inhibitory circuits of these QIF populations have been shown to exhibit sustained oscillatory activity [4], a single QIF population as described by Montbrio and colleagues cannot do so without periodic forcing. In this work, we extended the QIF model by a synaptic depression mechanism which weakens post-synaptic efficacies following pre-synaptic activity. The mechanism is independent of the specific synaptic model that is used and, in a globally coupled QIF network, can be coupled to the mean field such that each spike in the network triggers post-synaptic depression at all synapses. We demonstrate, that this synaptic depression mechanism can be well integrated into the macroscopic population description derived by Montbrio and colleagues and investigate its impact on the population dynamics. We show that, depending on the parametrization of synaptic depression, the QIF population can exhibit various forms of sustained oscillatory activity such as sinusoidal oscillations and bursting behavior. Furthermore, we provide a detailed description of the model’s bifurcation structure with regard to the synaptic depression. Finally, we provide an outlook in which scenarios this model could find application, i.e. which neurodynamic phenomena in the brain it could be linked to.

References

1.
Freeman, WJ. Mass Action in the Nervous System: Examination of the Neurophysiological Basis of Adaptive Behavior through the EEG. Academic Press London, 1975.
2.
Haken, H. Principles of Brain Functioning. Springer Berlin Heidelberg, 1996.
3.
Montbrió E, Pazó D, Roxin A. Macroscopic Description for Networks of Spiking Neurons. Physical Review X5 American Physical Society (APS) 2015.
4.
Schmidt H, Avitabile D, Montbrió E, Roxin A. Network mechanisms underlying the role of oscillations in cognitive tasks. Cold Spring Harbor Laboratory 2018.

P160 Prefrontal oscillations modulate the propagation of neuronal activity required for working memory

Jason Sherfey¹, Salva Ardid², Michael Hasselmo¹, Earl Miller³, Nancy Kopell²

¹Boston University, Psychological and Brain Sciences, Boston, MA, United States of America; ²Boston University, Mathematics and Statistics, Boston, MA, United States of America; ³Massachusetts Institute of Technology, The Picower Institute for Learning and Memory, Cambridge, United States of America

Correspondence: Jason Sherfey (sherfey@bu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P160

Cognition involves using attended information (e.g., stimuli, rules, responses), maintained in working memory (WM), to guide action. During a cognitive task, a correct response requires flexible, selective gating so that only the appropriate information flows at the proper time from WM to downstream effectors that carry out the response. Much evidence suggests that WM information is encoded in the firing rates of populations of neurons in prefrontal cortex (PFC). At the same time, many experiments have demonstrated separate, task-related modulation of oscillatory dynamics in PFC networks. In this work, we used biophysically-detailed modeling to explore the hypothesis that network oscillations, leveraging lateral inhibition, can independently gate responses to rate-coded items in working memory. Consistent with recent data, we modeled the superficial layers of PFC as a WM buffer that stores task-relevant information and the deep layers of PFC as an output gate that flexibly governs which information in the WM buffer is propagated downstream to guide action. We investigated two models of the WM buffer: one where items were stored in persistent spiking and one where items were stored synaptically. In the former “classic” model, item-encoding populations were in an asynchronous or rhythmic state modulated at fast beta/gamma oscillation frequencies. In the latter model, motivated by recent findings, items were stored in distributed connectivity patterns among populations with anatomically-motivated architecture; the synaptically-stored items were then made available for downstream propagation through the output gate by transient reactivation in a gamma-frequency rhythmic burst. In both cases, we found that whichever WM item induced a response in the output gate with the shortest period between spike volleys would be most reliably propagated through the output gate. Furthermore, the output gate exhibited network resonance capable of selectively propagating items with resonant oscillatory modulation. We found that network resonance of the deep layer gate can be flexibly tuned by varying the excitability of deep layer principal cells. Our results demonstrate that the propagation of WM-associated neuronal activity can be modulated by tuning either the oscillatory properties of populations encoding WM items, themselves, or the resonant properties of the output gate through which item-encoding activity must propagate to reach downstream effectors. In our PFC model, these dynamics reveal how population rate-coded items embedded in superficial beta and gamma oscillations can be alternately selected by tuning network resonance in the deep layers of PFC depending on task demands. Thus, our model predicts that the experimentally-observed modulation of PFC beta and gamma oscillations could leverage network resonance and lateral inhibition to govern the flexible routing of signals in service of cognitive processes like gating outputs from working memory and the selection of rule-based actions.

28th Annual Computational Neuroscience Meeting: CNS*2019

28th Annual Computational Neuroscience Meeting: CNS*2019

K1 Brain networks, adolescence and schizophrenia

Ed Bullmore

University of Cambridge, Department of Psychiatry, Cambridge, United Kingdom

Correspondence: Ed Bullmore (etb23@cam.ac.uk)

K2 Neural circuits for mental simulation

Kenji Doya

Okinawa Institute of Science and Technology, Neural Computation Unit, Okinawa, Japan

Correspondence: Kenji Doya (doya@oist.jp)

K3 One network, many states: varying the excitability of the cerebral cortex

Maria V. Sanchez-Vives

IDIBAPS and ICREA, Systems Neuroscience, Barcelona, Spain

Correspondence: Maria V. Sanchez-Vives (msanche3@clinic.cat)

K4 Neural circuits for flexible memory and navigation

Ila Fiete

Massachusetts Institute of Technology, McGovern Institute, Cambridge, United States of America

Correspondence: Ila Fiete (fiete@mit.edu)

F1 The geometry of abstraction in hippocampus and pre-frontal cortex

Silvia Bernardi1, Marcus K. Benna2, Mattia Rigotti3, Jérôme Munuera4, Stefano Fusi1, C. Daniel Salzman1

Correspondence: Marcus K. Benna (mkb2162@columbia.edu)

F2 Signatures of network structure in timescales of spontaneous activity

Roxana Zeraati1, Nicholas Steinmetz2, Tirin Moore3, Tatiana Engel4, Anna Levina5

Correspondence: Roxana Zeraati (roxana.zeraati@tuebingen.mpg.de)

F3 Internal bias controls phasic but not delay-period dopamine activity in a parametric working memory task

Néstor Parga1, Stefania Sarno1, Manuel Beiran2, José Vergara3, Román Rossi-Pool3, Ranulfo Romo3

1Universidad Autónoma Madrid, Madrid, Spain; 2Ecole Normale Supérieure, Department of Cognitive Studies, Paris, France; 3Universidad Nacional Autónoma México, Instituto de Fisiología Celular, México DF, Mexico

Correspondence: Néstor Parga (nestor.parga@uam.es)

O1 Representations of dissociated shape and category in deep Convolutional Neural Networks and human visual cortex

Astrid Zeman, J Brendan Ritchie, Stefania Bracci, Hans Op de Beeck

KULeuven, Brain and Cognition, Leuven, Belgium

Correspondence: Astrid Zeman (astrid.zeman@kuleuven.be)

O2 Discovering the building blocks of hearing: a data-driven, neuro-inspired approach

Lotte Weerts1, Claudia Clopath2, Dan Goodman1

1Imperial College London, Electrical and Electronic Engineering, London, United Kingdom; 2Imperial College London, Department of Bioengineering, London, United Kingdom

Correspondence: Dan Goodman (d.goodman@imperial.ac.uk)

O3 Modeling stroke and rehabilitation in mice using large-scale brain networks

Spase Petkoski1, Anna Letizia Allegra Mascaro2, Francesco Saverio Pavone2, Viktor Jirsa1

1Aix-Marseille Université, Institut de Neurosciences des Systèmes, Marseille, France; 2University of Florence, European Laboratory for Non-linear Spectroscopy, Florence, Italy

Correspondence: Spase Petkoski (spase.petkoski@univ-amu.fr)

O4 Self-consistent correlations of randomly coupled rotators in the asynchronous state

Alexander van Meegen1, Benjamin Lindner2

1Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6) and Institute for Advanced Simulation (IAS-6), Jülich, Germany; 2Humboldt University Berlin, Physics Department, Berlin, Germany

Correspondence: Alexander van Meegen (a.van.meegen@fz-juelich.de)

O5 Firing rate-dependent phase responses dynamically regulate Purkinje cell network oscillations

Yunliang Zang, Erik De Schutter

Okinawa Institute of Science and Technology, Computational Neuroscience Unit, Onna-Son, Japan

Correspondence: Yunliang Zang (zangyl1983@gmail.com)

O6 Computational modeling of brainstem-spinal circuits controlling locomotor speed and gait

Ilya Rybak, Jessica Ausborn, Simon Danner, Natalia Shevtsova

Drexel University College of Medicine, Department of Neurobiology and Anatomy, Philadelphia, PA, United States of America

Correspondence: Ilya Rybak (rybak@drexel.edu)

O7 Co-refinement of network interactions and neural response properties in visual cortex

Sigrid Trägenap1, Bettina Hein1, David Whitney2, Gordon Smith3, David Fitzpatrick2, Matthias Kaschube1

1Frankfurt Institute for Advanced Studies (FIAS), Department of Neuroscience, Frankfurt, Germany; 2Max Planck Florida Institute, Department of Neuroscience, Jupiter, FL, United States of America; 3University of Minnesota, Department of Neuroscience, Minneapolis, MN, United States of America

Correspondence: Sigrid Trägenap (traegenap@fias.uni-frankfurt.de)

O8 Receptive field structure of border ownership-selective cells in response to direction of figure

Ko Sakai1, Kazunao Tanaka1, Rüdiger von der Heydt2, Ernst Niebur3

1University of Tsukuba, Department of Computer Science, Tsukuba, Japan; 2Johns Hopkins University, Krieger Mind/Brain Institute, Baltimore, United States of America; 3Johns Hopkins, Neuroscience, Baltimore, MD, United States of America

Correspondence: Ko Sakai (sakai@cs.tsukuba.ac.jp)

O9 Development of periodic and salt-and-pepper orientation maps from a common retinal origin

Min Song, Jaeson Jang, Se-Bum Paik

Korea Advanced Institute of Science and Technology, Department of Biology and Brain Engineering, Daejeon, South Korea

Correspondence: Min Song (night@kaist.ac.kr)

O10 Explaining the pitch of FM-sweeps with a predictive hierarchical model

Alejandro Tabas1, Katharina von Kriegstein2

1Max Planck Institute for Human Cognitive and Brain Sciences, Research Group in Neural Mechanisms of Human Communication, Leipzig, Germany; 2Tesnische Universität Dresden, Chair of Clinical and Cognitive Neuroscience, Faculty of Psychology, Dresden, Germany

Correspondence: Alejandro Tabas (alextabas@gmail.com)

O11 Effects of anesthesia on coordinated neuronal activity and information processing in rat primary visual cortex

Heonsoo Lee, Shiyong Wang, Anthony Hudetz

University of Michigan, Anesthesiology, Ann Arbor, MI, United States of America

Correspondence: Heonsoo Lee (heonslee@umich.edu)

O12 Learning where to look: a foveated visuomotor control model

Emmanuel Daucé1, Pierre Albigès2, Laurent Perrinet3

1Aix-Marseille Univ, INS, Marseille, France; 2Aix-Marseille Univ, Neuroschool, Marseille, France; 3CNRS - Aix-Marseille Université, Institut de Neurosciences de la Timone, Marseille, France

Correspondence: Emmanuel Daucé (emmanuel.dauce@centrale-marseille.fr)

O13 A standardized formalism for voltage-gated ion channel models

Chaitanya Chintaluri1, Bill Podlaski2, Pedro Goncalves3, Jan-Matthis Lueckmann3, Jakob H. Macke3, Tim P. Vogels1

1University of Oxford, Centre for Neural Circuits and Behaviour, Oxford, United Kingdom; 2Champalimaud Center for the Unknown, Lisbon, Portugal; 3Research Center Caesar; Technical University of Munich, Bonn, Germany

Correspondence: Bill Podlaski (william.podlaski@gmail.com)

Silvia Bernardi¹, Marcus K. Benna², Mattia Rigotti³, Jérôme Munuera⁴, Stefano Fusi¹, C. Daniel Salzman¹

Roxana Zeraati¹, Nicholas Steinmetz², Tirin Moore³, Tatiana Engel⁴, Anna Levina⁵

Néstor Parga¹, Stefania Sarno¹, Manuel Beiran², José Vergara³, Román Rossi-Pool³, Ranulfo Romo³

¹Universidad Autónoma Madrid, Madrid, Spain; ²Ecole Normale Supérieure, Department of Cognitive Studies, Paris, France; ³Universidad Nacional Autónoma México, Instituto de Fisiología Celular, México DF, Mexico

Lotte Weerts¹, Claudia Clopath², Dan Goodman¹

¹Imperial College London, Electrical and Electronic Engineering, London, United Kingdom; ²Imperial College London, Department of Bioengineering, London, United Kingdom

Spase Petkoski¹, Anna Letizia Allegra Mascaro², Francesco Saverio Pavone², Viktor Jirsa¹

¹Aix-Marseille Université, Institut de Neurosciences des Systèmes, Marseille, France; ²University of Florence, European Laboratory for Non-linear Spectroscopy, Florence, Italy

Alexander van Meegen¹, Benjamin Lindner²

¹Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6) and Institute for Advanced Simulation (IAS-6), Jülich, Germany; ²Humboldt University Berlin, Physics Department, Berlin, Germany

Sigrid Trägenap¹, Bettina Hein¹, David Whitney², Gordon Smith³, David Fitzpatrick², Matthias Kaschube¹

¹Frankfurt Institute for Advanced Studies (FIAS), Department of Neuroscience, Frankfurt, Germany; ²Max Planck Florida Institute, Department of Neuroscience, Jupiter, FL, United States of America; ³University of Minnesota, Department of Neuroscience, Minneapolis, MN, United States of America

Ko Sakai¹, Kazunao Tanaka¹, Rüdiger von der Heydt², Ernst Niebur³

¹University of Tsukuba, Department of Computer Science, Tsukuba, Japan; ²Johns Hopkins University, Krieger Mind/Brain Institute, Baltimore, United States of America; ³Johns Hopkins, Neuroscience, Baltimore, MD, United States of America

Alejandro Tabas¹, Katharina von Kriegstein²

¹Max Planck Institute for Human Cognitive and Brain Sciences, Research Group in Neural Mechanisms of Human Communication, Leipzig, Germany; ²Tesnische Universität Dresden, Chair of Clinical and Cognitive Neuroscience, Faculty of Psychology, Dresden, Germany

Emmanuel Daucé¹, Pierre Albigès², Laurent Perrinet³

¹Aix-Marseille Univ, INS, Marseille, France; ²Aix-Marseille Univ, Neuroschool, Marseille, France; ³CNRS - Aix-Marseille Université, Institut de Neurosciences de la Timone, Marseille, France

Chaitanya Chintaluri¹, Bill Podlaski², Pedro Goncalves³, Jan-Matthis Lueckmann³, Jakob H. Macke³, Tim P. Vogels¹

¹University of Oxford, Centre for Neural Circuits and Behaviour, Oxford, United Kingdom; ²Champalimaud Center for the Unknown, Lisbon, Portugal; ³Research Center Caesar; Technical University of Munich, Bonn, Germany

Camille Gontier¹, Jean-Pascal Pfister²

¹University of Bern, Department of Physiology, Bern, France; ²University of Bern, Department of Physiology, Bern, Switzerland

Ernest Montbrió¹, Alex Roxin², Federico Devalle¹, Bastian Pietras³, Andreas Daffertshofer³

¹Universitat Pompeu Fabra, Department of Information and Communication Technologies, Barcelona, Spain; ²Centre de Recerca Matemàtica, Barcelona, Spain; ³Vrije Universiteit Amsterdam, Behavioral and Movement Sciences, Amsterdam, Netherlands

Gal Mishne¹, Benjamin Scott², Stephan Thiberge⁴, Nathan Cermak³, Jackie Schiller³, Carlos Brody⁴, David W. Tank⁴, Adam Charles⁴

¹Yale University, Applied Math, New Haven, CT, United States of America; ²Boston University, Boston, United States of America; ³Technion, Haifa, Israel; ⁴Princeton University, Department of Neuroscience, Princeton, NJ, United States of America

James Jun¹, Jeremy Magland¹, Catalin Mitelut², Alex Barnett¹

¹Flatiron Institute, Center for Computational Mathematics, New York, NJ, United States of America; ²Columbia University, Department of Statistics, New York, United States of America

Davd Bestue¹, Albert Compte², Torkel Klingberg³, Rita Almeida⁴

¹IDIBAPS, Barcelona, Spain; ²IDIBAPS, Systems Neuroscience, Barcelona, Spain; ³Karolinksa Institutet, Stockholm, Sweden; ⁴Stockholm University, Stockholm, Sweden

Cecilia Romaro¹, Fernando Najman², Morgan Andre²

¹University of São Paulo, Department of Physics, Ribeirão Preto, Brazil; ²University of São Paulo, Institute of Mathematics and Statistics, São Paulo, Brazil

Tuomo Mäki-Marttunen¹, Gaute Einevoll², Anna Devor³, William A. Phillips⁴, Anders M. Dale³, Ole A. Andreassen⁵

Marina Charquero¹, Morten L Kringelbach¹, Birgit Kleim², Christian Ruff³, Steven C.R Williams⁴, Mark Woolrich⁵, Vidaurre Diego⁵, Ehlers Anke⁶

Peng Gao¹, Joe Graham², Wen-Liang Zhou¹, Jinyoung Jang¹, Sergio Angulo², Salvador Dura-Bernal², Michael Hines³, William W Lytton², Srdjan Antic¹

Sára Sáray¹, Christian A Rössert², Andrew Davison³, Eilif Muller², Tamas Freund⁴, Szabolcs Kali⁴, Shailesh Appukuttan³

Yazan Billeh¹, Binghuang Cai², Sergey Gratiy¹, Kael Dai¹, Ramakrishnan Iyer¹, Nathan Gouwens¹, Reza Abbasi-Asl², Xiaoxuan Jia³, Joshua Siegle¹, Shawn Olsen¹, Christof Koch¹, Stefan Mihalas¹, Anton Arkhipov¹

¹Allen Institute for Brain Science, Modelling, Analysis and Theory, Seattle, WA, United States of America; ²Allen Institute for Brain Science, Seattle, WA, United States of America; ³Allen Institute for Brain Science, Neural Coding, Seattle, WA, United States of America

Kentaro Suzuki¹, Jihoon Park², Yuji Kawai², Minoru Asada²

¹Osaka University, Graduate School of Engineering, Minoh City, Japan; ²Osaka University, Suita, Osaka, Japan

Zachary Sheldon¹, Ronald DiTullio², Vijay Balasubramanian²

¹University of Pennsylvania, Philadelphia, PA, United States of America; ²University of Pennsylvania, Computational Neuroscience Initiative, Philadelphia, United States of America

Viktor Sip¹, Viktor Jirsa¹, Maxime Guye², Fabrice Bartolomei³

¹Aix-Marseille Universite, Institute de Neurosciences, Marseille, France; ²Aix-Marseille Université, Centre de Résonance Magnétique Biologique et Médicale, Marseille, France; ³Assistance Publique - Hôpitaux de Marseille, Service de Neurophysiologie Clinique, Marseille, France